用Tupper自我指涉公式造图
塔珀自指公式是杰夫·塔珀(Jeff Tupper)发现的自指公式:此公式的二维图像与公式本身外观一样。此公式在众多数学与计算机科学课程里被用作绘制公式图像的练习作业。
4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300
@鄙视下维基百科给出的k是错的
时,然后将在和所示范围中符合以上不等式的点(x,y-k)绘制出来,结果会是这样:
函数的结果是函数本身图像,其实这个函数可以绘制任何图像,然后发给你心爱的人说,我发现个函数,k=多少多少时,会出现love you之类的,
我果然是理科生....=.=
过程是这样的,
- 我们绘制一个单色位图
- 然后我们将位图转换为2进制数值
- 逆向这个公式得到k
- =.= 检查图形美不美
1. 打开个文本
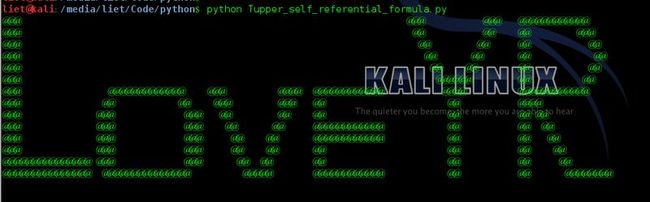
在107*17的范围内绘制图形如下,love YR ,哈哈YR是谁呢,注意长宽空格都算在内的
2.上代码,tupper.txt就是上面的文件
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 import math 4 5 def Base2_to_10(x): 6 ans = 0 7 i = 0 8 while x > 0: 9 if x%10 == 1: ans += 2**i 10 x /= 10 11 i += 1 12 return ans 13 def input(): 14 bar = "" 15 for line in open('tupper.txt'): 16 for i in line[:-1]: 17 bar += i 18 code = ["0" for i in xrange(17*107)] 19 for i in xrange(17*107-1): 20 #print i 21 x = i%107 22 y = 16- i/107 23 if bar[i] == "0": 24 code[17*x+y] = "1" 25 str = "".join(code) 26 return Base2_to_10(int(str[::-1]))*17 27 str = input() 28 print str
3 得到str
17395801135847186519514533766577166712920244599511619806806360198319443964624090437973069690063751432629635277541067512742591237154706476089604919941282726117482657226986792284460049763364287128660374652834353819138510460422151182573412890443751441495242184763277437223648251193921175808287491778837040326348124920816742193510432149378864985078857052059037920621670314430604882179347284818468370754314529752114472995398250019563369691397252465478396117000433401686853725151310746693542808908025107928533841248521147887035746484088
4.用官方的代码跑一下效果
1 """ 2 Copyright (c) 2012, 2013 The PyPedia Project, http://www.pypedia.com 3 <br>All rights reserved. 4 5 Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met: 6 7 # Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. 8 # Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution. 9 10 THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND 11 ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED 12 WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE 13 DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR 14 ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES 15 (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; 16 LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND 17 ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT 18 (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS 19 SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE. 20 21 http://www.opensource.org/licenses/BSD-2-Clause 22 """ 23 24 __pypdoc__ = """ 25 Method: Tupper_self_referential_formula 26 Link: http://www.pypedia.com/index.php/Tupper_self_referential_formula 27 Retrieve date: Tue, 11 Mar 2014 03:15:49 +0200 28 29 30 31 Plots the [http://en.wikipedia.org/wiki/Tupper's_self-referential_formula Tupper's_self-referential_formula]: 32 : <math>{1\over 2} < \left\lfloor \mathrm{mod}\left(\left\lfloor {y \over 17} \right\rfloor 2^{-17 \lfloor x \rfloor - \mathrm{mod}(\lfloor y\rfloor, 17)},2\right)\right\rfloor</math> 33 34 The plot is the very same formula that generates the plot. 35 36 [[Category:Validated]] 37 [[Category:Algorithms]] 38 [[Category:Math]] 39 [[Category:Inequalities]] 40 41 42 """ 43 44 def Tupper_self_referential_formula(): 45 k = 17395801135847186519514533766577166712920244599511619806806360198319443964624090437973069690063751432629635277541067512742591237154706476089604919941282726117482657226986792284460049763364287128660374652834353819138510460422151182573412890443751441495242184763277437223648251193921175808287491778837040326348124920816742193510432149378864985078857052059037920621670314430604882179347284818468370754314529752114472995398250019563369691397252465478396117000433401686853725151310746693542808908025107928533841248521147887035746484088 46 #love yiran 47 48 49 def f(x,y): 50 d = ((-17 * x) - (y % 17)) 51 e = reduce(lambda x,y: x*y, [2 for x in range(-d)]) if d else 1 52 f = ((y / 17) / e) 53 g = f % 2 54 return 0.5 < g 55 56 for y in range(k+16, k-1, -1): 57 line = "" 58 for x in range(0, 107): 59 if f(x,y): 60 line += "@" 61 else: 62 line += " " 63 print line 64 65 66 #Method name =Tupper_self_referential_formula() 67 if __name__ == '__main__': 68 # print __pypdoc__ 69 70 returned = Tupper_self_referential_formula() 71 if returned: 72 print str(returned)
5.得到效果
love 依然~~
参考:
http://www.matrix67.com/blog/archives/301
http://www.zhihu.com/question/22506052/answer/21583549
http://zh.wikipedia.org/wiki/%E5%A1%94%E7%8F%80%E8%87%AA%E6%8C%87%E5%85%AC%E5%BC%8F