poj2986A Triangle and a Circle&&poj3675Telescope（三角形剖分）

链接

2986是3675的简化版，只有一个三角形。

这题主要在于求剖分后三角形与圆的相交面积，需要分情况讨论。

具体可以看此博客 http://hi.baidu.com/billdu/item/703ad4e15d819db52f140b0b

在分析第3、4两种情况时，我是用角度来进行判断的，如果<obc||<ocb大于90度就为他所说的第四种情况，不然就是第三种情况。

还有对于sig的解释貌似网上都没写，可能都觉得太简单了。。。自己手画了一下，大体是这个样子的

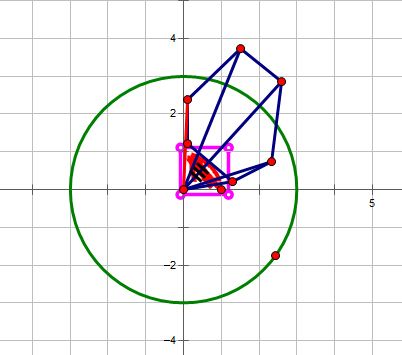红色标记那块三角形是需要减掉对于当前多边形，可以看出以最下角进行剖分三角形时，cross(b,c)算的那块小三角形的确是负的，所以需要判断一下当前的面积是要加上的还是要减掉的。

讨论的东西比较多，细节比较多，WA了好多遍，对着数据查了好久终于过了。。

附上一些数据

  1 #include <iostream>

  2 #include<cstdio>

  3 #include<cstring>

  4 #include<algorithm>

  5 #include<stdlib.h>

  6 #include<vector>

  7 #include<cmath>

  8 #include<queue>

  9 #include<set>

 10 using namespace std;

 11 #define N 100

 12 #define LL long long

 13 #define INF 0xfffffff

 14 const double eps = 1e-8;

 15 const double pi = acos(-1.0);

 16 const double inf = ~0u>>2;

 17 struct point

 18 {

 19     double x,y;

 20     point(double x=0,double y=0):x(x),y(y) {}

 21 } p[N];

 22 struct tri

 23 {

 24     point a,b,c;

 25 } tr[N];

 26 typedef point pointt;

 27 point operator -(point a,point b)

 28 {

 29     return point(a.x-b.x,a.y-b.y);

 30 }

 31 point operator *(point a,double r)

 32 {

 33     return point(a.x*r,a.y*r);

 34 }

 35 point operator +(point a,point b)

 36 {

 37     return point(a.x+b.x,a.y+b.y);

 38 }

 39 struct line

 40 {

 41     point u,v;

 42     point ppoint(double t)

 43     {

 44         return point(u+v*t);

 45     }

 46 };

 47 struct circle

 48 {

 49     point c;

 50     double r;

 51     circle(point c,double r):c(c),r(r) {}

 52     point ppoint(double a)

 53     {

 54         return point(c.x+cos(a)*r,c.y+sin(a)*r);

 55     }

 56 };

 57 double r;

 58 point ip;

 59 double dcmp(double x)

 60 {

 61     if(fabs(x)<eps) return 0;

 62     return x<0?-1:1;

 63 }

 64 double dis(point a)

 65 {

 66     return sqrt(a.x*a.x+a.y*a.y);

 67 }

 68 double dot(point a,point b)

 69 {

 70     return a.x*b.x+a.y*b.y;

 71 }

 72 double cross(point a,point b)

 73 {

 74     return a.x*b.y-a.y*b.x;

 75 }

 76 double area(point a,point b,point c)

 77 {

 78     return fabs(cross(a-c,b-c))/2;

 79 }

 80 

 81 int getlinecircle(line ll,circle cc,point &p1,point &p2)

 82 {

 83     double a = ll.v.x,b = ll.u.x-cc.c.x,c = ll.v.y,d = ll.u.y-cc.c.y;

 84     double e = a*a+c*c,f = 2*(a*b+c*d),g = b*b+d*d-cc.r*cc.r;

 85     double delta = f*f-4*e*g;

 86     double t1,t2;

 87     if(dcmp(delta)<0)return 0;//ÏàÀë

 88     if(dcmp(delta)==0)

 89     {

 90         t1 = t2 = -f/(2*e);//cout<<t1<<" -"<<e<<" "<<f<<endl;

 91         p1 = ll.ppoint(t1);

 92         return 1;//ÏàÇÐ

 93     }

 94     //Ïཻ

 95     t1 = (-f-sqrt(delta))/(2*e);

 96     p1 = ll.ppoint(t1);

 97     t2 = (-f+sqrt(delta))/(2*e);

 98     p2 = ll.ppoint(t2);

 99     // cout<<p1.x<<" "<<p1.y<<" "<<p2.x<<" "<<p2.y<<endl;

100     return 2;

101 }

102 double mul(point a,point b,point c)

103 {

104     return cross(b-a,c-a);

105 }

106 bool cmp(point a,point b)

107 {

108     if(dcmp(mul(ip,a,b))==0)

109         return dis(a-ip)<dis(b-ip);

110     else

111         return dcmp(mul(ip,a,b))>0;

112 }

113 double distancetoline(point p,point a,point b)

114 {

115     point v1 = a-b,v2 = p-b;

116     return fabs(cross(v1,v2))/dis(v1);

117 }

118 int dot_online_in(point p,point l1,point l2)

119 {

120     return !dcmp(mul(p,l1,l2))&&(l1.x-p.x)*(l2.x-p.x)<eps&&(l1.y-p.y)*(l2.y-p.y)<eps;

121 }

122 double angle(point a,point b)

123 {

124     return acos(dot(a,b)/dis(a)/dis(b));

125 }

126 double cal(tri tr)

127 {

128     circle cp=circle(point(0,0),r);

129     int sig = dcmp(cross(tr.b,tr.c));

130     if(sig==0) return 0;

131     double d1 = dis(tr.a-tr.b),d2 = dis(tr.a-tr.c);

132     if(dcmp(d1-r)<=0&&dcmp(d2-r)<=0)

133     {

134         double s = sig*area(tr.a,tr.b,tr.c);

135         return s;

136     }

137     double dline = distancetoline(cp.c,tr.b,tr.c);

138     if(dcmp(d1-r)>=0&&dcmp(d2-r)>=0&&dcmp(dline-r)>=0)

139     {

140         return sig*angle(tr.b,tr.c)*r*r/2.0;

141     }

142     double ag = angle(tr.c-tr.b,tr.a-tr.b),bg = angle(tr.b-tr.c,tr.a-tr.c);

143     point p1,p2;

144     line l1;

145     l1.u = tr.b,l1.v = tr.c-tr.b;

146     getlinecircle(l1,cp,p1,p2);

147 

148     if(dcmp(d1-r)>=0&&dcmp(d2-r)>=0&&dcmp(dline-r)<0&&(dcmp(ag-pi/2)>=0||dcmp(bg-pi/2)>=0))

149     {

150 

151         double s = sig*angle(tr.b,tr.c)*r*r/2;

152         return s;

153     }

154     if(dcmp(d1-r)>=0&&dcmp(d2-r)>=0&&dcmp(dline-r)<0)

155     {

156         double s = (angle(tr.b,tr.c)-angle(p1,p2))*r*r/2.0+area(tr.a,p1,p2);

157         return sig*s;

158     }

159 

160     p1 = dot_online_in(p1,tr.b,tr.c)?p1:p2;

161     if(dcmp(d1-r)<0)

162     {

163         return sig*(angle(tr.c,p1)*r*r/2+area(tr.a,p1,tr.b));

164     }

165     else

166     {

167         return sig*(angle(p1,tr.b)*r*r/2+area(tr.a,p1,tr.c));

168     }

169 }

170 int dots_inline(point p1,point p2,point p3)

171 {

172     return !dcmp(mul(p1,p2,p3));

173 }

174 int main()

175 {

176     int i,n;

177     while(scanf("%lf",&r)!=EOF)

178     {

179         scanf("%d",&n);

180         for(i = 0; i < n ; i++)

181         {

182             scanf("%lf%lf",&p[i].x,&p[i].y);

183         }

184         p[n] = p[0];

185         double ans = 0;

186         for(i = 0 ; i < n ; i++)

187         {

188             if(dots_inline(ip,p[i],p[i+1])) continue;

189             tr[i].a = point(0,0);

190             tr[i].b = p[i];

191             tr[i].c = p[i+1];

192             ans+=cal(tr[i]);

193         }

194         printf("%.2f\n",fabs(ans)+eps);

195     }

196     return 0;

197 }

View Code

589.00 191.00 -554.00 710.00 748.00 774.00 -888.00 -588.00 902.00

201.00 -847.00 -365.00 886.00 -557.00 -609.00 272.00 -345.00 189.00

-358.00 981.00 269.00 511.00 158.00 -304.00 468.00 463.00 834.00

969.00 514.00 -445.00 460.00 -177.00 774.00 -34.00 -125.00 162.00

-467.00 413.00 -714.00 -986.00 362.00 666.00 813.00 271.00 264.00

-497.00 908.00 -414.00 631.00 -220.00 868.00 166.00 -258.00 306.00

-107.00 -743.00 -952.00 322.00 -273.00 -214.00 -14.00 466.00 758.00

511.00 -416.00 -934.00 -745.00 -335.00 -132.00 -482.00 391.00 626.00

928.00 821.00 -293.00 -853.00 -488.00 -312.00 -27.00 94.00 361.00

-979.00 -280.00 791.00 -943.00 -300.00 -278.00 -821.00 684.00 365.00

-700.00 955.00 -315.00 154.00 -103.00 -606.00 404.00 -792.00 940.00

607.00 783.00 597.00 944.00 -672.00 -323.00 343.00 -799.00 526.00

815.00 -390.00 -291.00 37.00 422.00 687.00 672.00 613.00 848.00

-988.00 363.00 -529.00 660.00 -597.00 143.00 502.00 459.00 522.00

-206.00 484.00 109.00 -111.00 424.00 650.00 330.00 -545.00 480.00

94.00 -638.00 -59.00 -9.00 -400.00 -702.00 0.00 267.00 741.00

-859.00 522.00 109.00 -640.00 383.00 712.00 489.00 -663.00 635.00

808.00 -31.00 471.00 172.00 -374.00 21.00 120.00 -860.00 474.00

-539.00 -887.00 498.00 844.00 -453.00 -213.00 -479.00 -9.00 315.00

 

 

答案

Case 1
0.00
Case 2
0.00
Case 3
274955.27
Case 4
0.00
Case 5
0.00
Case 6
0.00
Case 7
25157.17
Case 8
9943.87
Case 9
181113.99
Case 10
0.00
Case 11
11846.16
Case 12
0.00
Case 13
404668.37
Case 14
0.00
Case 15
0.00
Case 16
74663.53
Case 17
80015.79
Case 18
0.00
Case 19
57316.85
Case 20
0.00