【算法与数据结构】图说堆排序
1、堆 一棵完全二叉树
大顶堆:所有非叶子节点元素均不小于其左右子树根节点的值
小顶堆:所有非叶子节点元素均不大于其左右子树根节点的值
2、 初始化堆
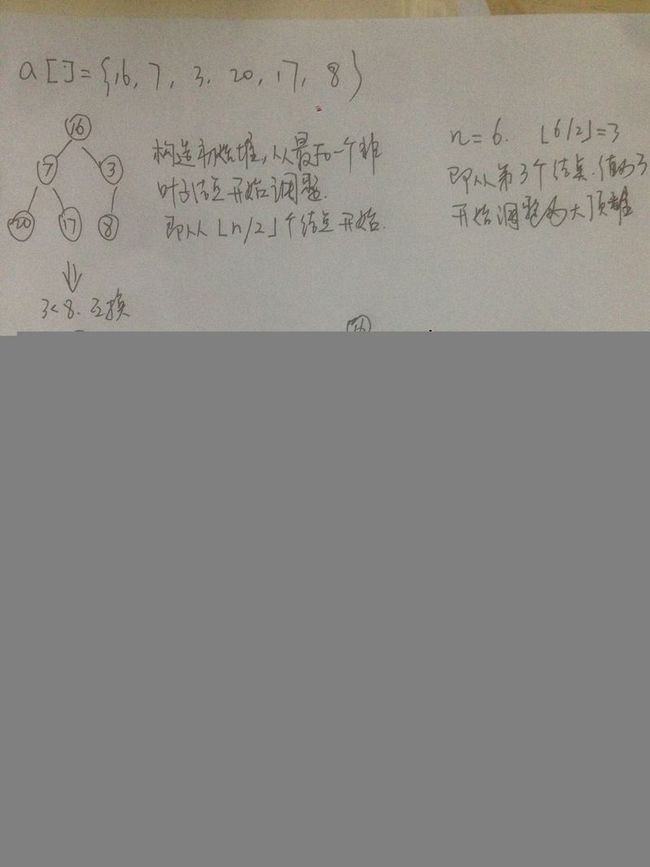
①一组无序元素R[0, 1, ..., n - 1], 先按照顺序将该组无序元素构造为一棵完全二叉树
②从该二叉树的第一个非叶子结点开始调整,然后调整前一个结点(一定是非叶子结点),依次直到调整完根节点
③上一步一遍完成后,再来一遍,直到该完全二叉树符合一个堆的定义为止
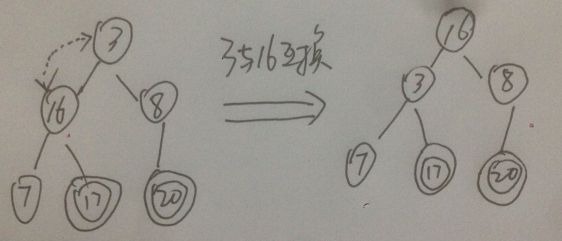
测试数据:R[] = {16, 7, 3, 20, 17, 8}, 本组测试数据中,最后一个非叶子结点为值为3的点
3、调整堆
第二步完成后,二叉树符合一个堆的定义,如下图
步骤:
将符合堆定义的上图中最后一个元素 与 堆顶元素互换, 此时集合 { R[n - 1] }有序, 剩下的无序序列为{ R[0, ..., n - 2] }
互换后,如果堆顶元素不符合堆的定义,则对齐进行调整:此父结点 与 左右子树根节点中 大的那个 互换, 再调整其他不符合堆定义的元素
当{ R[0, ..., n - 2] }中元素都符合堆定义的时候,将最后一个元素(即 R[n - 2])与堆顶元素互换, 此时 集合{ R[n - 2], R[n - 1] }有序,
重复上述过程
具体如下
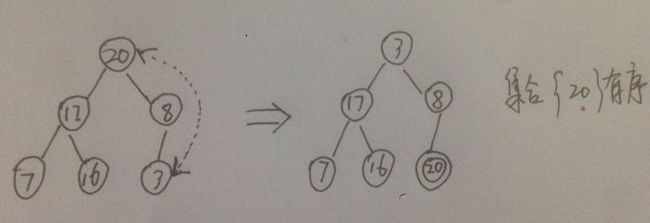
①将二叉树的最后一个结点(图中值为3的点) 与 堆顶元素 互换位置, 此时 集合 {20}有序
② 堆顶元素3不符合堆定义,调整
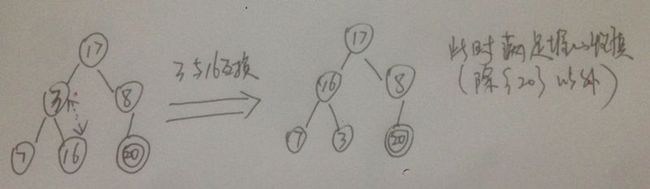
③此时元素3 不符合堆定义, 调整
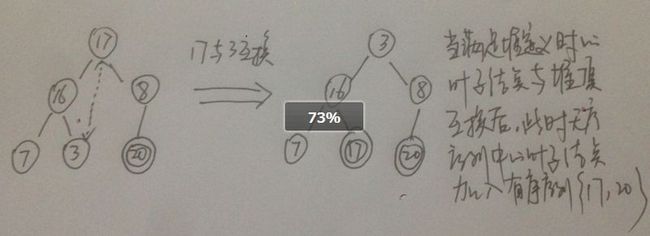
④二叉树满足堆的定义后,将无序序列中最后一个元素(这里应该是值为3的元素) 与 堆顶元素 互换
⑤此时的有序序列为 {17, 20}, 此时堆顶元素3不满足堆定义,调整
⑥此时 元素3 不满足堆定义,调整
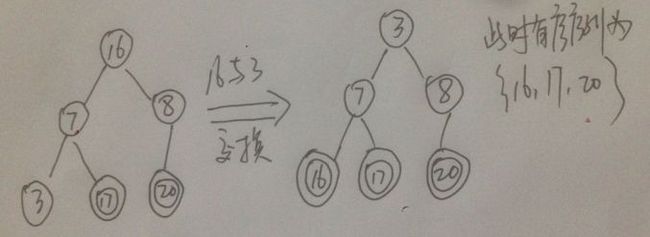
⑦此时除有序序列{17, 20}以外,其余元素满足堆定义, 将无序序列中最后一个结点(这里是值为3的元素) 与 堆顶元素 互换
⑧此时 有序序列为{16, 17, 20}, 堆顶元素3不满足堆定义, 调整
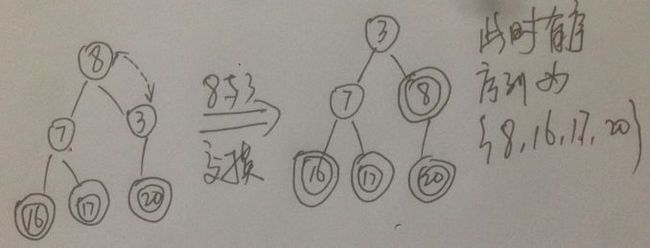
⑨此时除有序序列{16, 17, 20}以外,剩余无序序列满足堆定义, 将无序序列中最后一个元素(值为3的元素) 与 堆顶元素 互换
⑩此时有序序列为 {8, 16,17, 20}, 堆顶元素3不满足堆定义, 调整
⑾此时除有序序列{8, 16, 17, 20}以外, 剩余元素满足堆定义, 将无序序列中最后一个元素(值为3的元素) 与 堆顶 互换
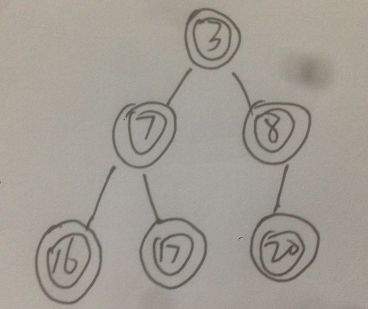
⑿此时有序序列为{7, 8, 16, 17, 20}, 无序序列中只剩一个元素, 调整完毕,如下
完毕。
参考文献:http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html 感谢作者