模拟试题A
模拟试题A
一、单项选择题(2′*12=24′)
1.下面各种坐标变换中,会产生变换前后维度的改变的是( )
A)建模变换 B)观察变换 C)投影变换 D)视口变换
2.下列描述深度缓冲消隐算法的特点中,正确的是( )
A)从每个多边形出发,根据其对应像素深度大小比较,严格按自远到近顺序进行显示
B)以视区每个像素为处理对象,严格按自远到近顺序进行显示
C)从每个多边形出发,根据其对应像素深度大小比较,可按任意顺序进行显示
D)以视区每个像素为处理对象,可按任意顺序进行显示
3.下列消隐算法中,与其它三个算法所属消隐空间不同的是( )
A)画家算法 B)Z-Buffer算法C)扫描线Z-Buffer算法 D)光线跟踪算法
4.三维Cohen-Surtherland裁剪算法中直线端点编码需要多少位?( )
A)3 B)4 C)6 D)8
5.多边形扫描线填充算法四个步骤中,保证填充无误的关键步骤是( )
A)求交点 B)对交点排序 C)交点配对 D)交点所在区间填色
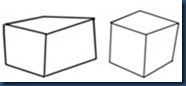
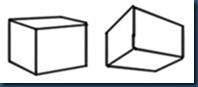
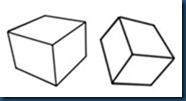
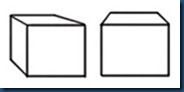
6.下图中四组正方体透视图错误的一组是 ( )
7.假设场景中有k个多边形构成,显示分辨率为m*n,则图像空间消隐算法的算法复杂度为 ( )
A)k*k B)m*n C)m*n*k D)m*n*k*k
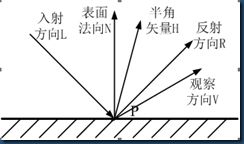
8.如图B.1所示,则反射方向矢量R为( )
9.如图B.1所示,则不完全镜面反射光Is 的计算式![]() 中θ为( )
中θ为( )
A)N与H的夹角 B)R与N的夹角 C)R与V的夹角 D)R与H的夹角
图B.1 光的反射
10.下列有关透视投影的叙述,错误的是( )
A)投影后会发生变形 B)至多只能有三个灭点
C)投影线过视点 D)视觉效果比平行投影更具真实感
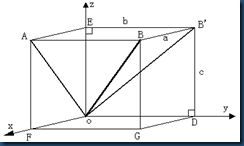
11.图B.2中,欲使OB绕x轴旋转至xoz坐标平面内,旋转角度为( )
A)∠AOB B)∠EOB C)∠EOB′ D)∠FOB
图B.2 旋转变换
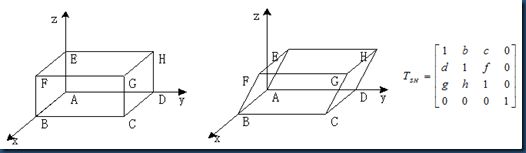
12.若图B.3中,自左图变为中间图形所对应变换为错切变换![]() ,其错切变换矩阵如右下方所示,则其中系数不等于0是( )
,其错切变换矩阵如右下方所示,则其中系数不等于0是( )
A)d, g B)b, h C)c, f D) d, f
图B.3 错切变换
二、多项选择题(2′*7=14′)
1.下列二维基本变换类型中,能以坐标原点为变换参考对象的是( )
A)平移变换 B)旋转变换 C)比例变换 D)错切变换
2.下列有关物体的几何表示法的叙述语句中,正确的为( )
A)在计算机图形学中,通常所谓“物体”是三维欧氏空间点的集合
B)一组三维欧氏空间点的集合都可看成一个(组)“物体”
C)单个孤立的点不是“物体”
D)一根直线段或单张曲面都是“物体”
3.不能很好地处理透明对象的消隐算法是( )
A)画家算法 B)Z-Buffer算法 C)扫描线Z-Buffer算法 D)光线跟踪算法
4.下列语句中,错误的论述为( )
A)为了消除闪烁现象隔行扫描技术逐步取代了逐行扫描技术
B)彩色打印机使用RGB颜色模型
C)光栅扫描图形显示器中,所有对象都应转化为像素点来显示
D)在图形文件中,点、线、圆、弧等图形元素都要转化为像素点来描述
5.下面哪些措施能获得反走样效果?( )
A)把像素当作平面区域进行采样 B)提高分辨率
C)采用锥形滤波器进行加权区域采样 D)增强图像的显示亮度
6.下面各种坐标变换中,有两个变换类型性质都属于3D→3D变换,它们是( )
A)建模变换 B)观察变换 C)投影变换 D)视口变换
7.下面各项中,属于明暗处理技术的有( )
A)Flat平坦方法 B)Gouraud方法 C)Phong方法 D)Lambert方法
三、填空题(2′*9=18′)
1. 计算机图形学三个核心领域为 、 和 。
2. 任意的简单多面体,其面(F)、边(E)、顶点(V)的数目需满足的公式为 。
3. 显示器分辨率m*n,颜色数K与显存大小V之间的关系式为 。
4. 字符图形常见有两种表示方法,分别是 、 。
5. 点阵表示的区域常见有两种表示形式,分别是 、
6. 编码裁剪算法中,若线段两端点编码位相与运算结果不为0,表明线段与窗口的关系是_________。
7.光栅扫描显示系统主要由三部分组成,分别是 、 、和 。
8. 对于GB2312-80所规定的6763个基本汉字,设每个汉字是72*72点阵,那么一个字库需要存储空间=__________________=__________字节(前面填计算式,后面写结果)
9. 设窗口的四条边界为![]() ,视区的四条边界为
,视区的四条边界为![]() 已知窗口内的一点(Xw,Yw),则对应视区中的点(Xs,Ys)为Xs= ,Ys= 。
已知窗口内的一点(Xw,Yw),则对应视区中的点(Xs,Ys)为Xs= ,Ys= 。
四、综合题(44′)
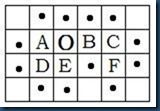
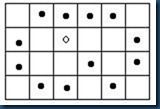
1. 图B.4中,左图表示由小圆点包围形成一四连通区域,其中已知种子O,其余点标记为A,B,C,D,E,F。(10分)
(1)试根据简单四连通种子填充算法按左、上、右、下入栈的顺序给出像素点填充的次序,用序号123456将填充次序结果在右图中标出(4′);
图B.4 区域填充
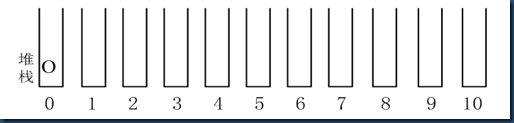
(2)将填充过程中每一步堆栈中的内容按所给字母标记填写在下图所示堆栈中(6′)。
图B.5 堆栈
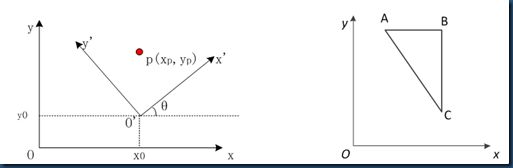
2. 已知p点在xoy坐标系下坐标为![]() , 试用齐次坐标求新坐标系x′o′y′下的坐标
, 试用齐次坐标求新坐标系x′o′y′下的坐标![]() 。两坐标系的相对关系如下图所示,要求写出每一步变换过程(6′),给出每一步计算结果(6′)(12分)
。两坐标系的相对关系如下图所示,要求写出每一步变换过程(6′),给出每一步计算结果(6′)(12分)
图B.6 坐标变换 图B.7 三角形变换
3. 已知图B.7中所示三角形ABC各顶点的坐标A(2,4)、B(4,4)、C(4,1),相对A点逆时针旋转600,各顶点分别到达A'、B'、C'。试计算A'、B'、C'的坐标值。(要求用齐次坐标进行变换,列出变换矩阵。)(10分)
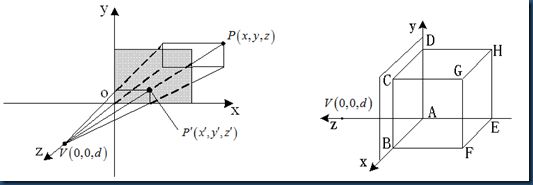
4. 设视点在z轴(0,0,d)处,试推导P点的透视变换矩阵。要求最后保留深度信息(5′)。 若已知单位立方体如图B.8所示放置,根据透视变换矩阵计算各顶点透视变换后的顶点坐标(7′)。(12分)
图B.8 透视变换