A Blind Watermarking for 3-D Dynamic Mesh Model Using Distribution of Temporal Wavelet Coefficients
这周看了一篇动态网格序列水印的论文,由于目前在网格序列上做水印的工作特别少,加之我所看的这篇论文中的叙述相对简洁,理解起来颇为困难。好在请教了博士师兄,思路明朗了许多,也就把这思路整理在此了。
论文作者提出了一种三维网格序列盲水印算法,在他们的算法中用到了小波分析。我对小波分析只有一个大概的了解,所以细节的理解上可能不尽正确,索性就不详细解释小波分解的知识了。
首先介绍论文中水印的产生:
此篇论文中的水印为 W= +1 或 W = -1,具体位数上嵌入+1还是 -1 作者没有做详细解释
然后介绍水印的嵌入:
对于原始的3-D序列![]() 其中N为帧总数),每一帧的重心都平移到坐标原点,作为计算小波系数的预处理。
其中N为帧总数),每一帧的重心都平移到坐标原点,作为计算小波系数的预处理。
第一步,每个点的坐标使用小波变换沿着时间轴平移。原始序列被分解为低频序列![]() ,称为比例系数,和高频序列
,称为比例系数,和高频序列![]() ,称为小波系数。
,称为小波系数。
本文中用到了bin的概念,它是水印嵌入的单位。每个bin从平均帧![]() 分裂而来,
分裂而来,![]() 是
是![]() 的平均数。
的平均数。![]() 的笛卡尔坐标
的笛卡尔坐标![]() 被转换为球面坐标
被转换为球面坐标![]() ,
,
笛卡尔坐标与球面坐标相互转换公式:(参考Wavelet transform based digital watermarking for 3-D surface meshes and mesh sequences)
![]()
其中i是顶点索引,![]() 是
是![]() 的法向。根据
的法向。根据![]() 的概率分布的大小,将这些概率分布划分到M个独立的、范围相同的bin中。在第m个bin中的顶点i将用于保存该顶点相应的修改后的小波系数。
的概率分布的大小,将这些概率分布划分到M个独立的、范围相同的bin中。在第m个bin中的顶点i将用于保存该顶点相应的修改后的小波系数。
属于第m个bin的小波系数![]() 被映射到[-1,1]这个归一化区间。现在,每个bin在区间[-1,1]上都有一个拉普拉斯分布。为了嵌入第m个水印比特
被映射到[-1,1]这个归一化区间。现在,每个bin在区间[-1,1]上都有一个拉普拉斯分布。为了嵌入第m个水印比特![]() 方差为
方差为![]() 的归一化后的小波系数
的归一化后的小波系数![]() 将由一个因子+△(或 –△)修改,修改方式如下:
将由一个因子+△(或 –△)修改,修改方式如下:
其中,![]() 分别表示
分别表示![]() 负数部分和正数部分的方差,
负数部分和正数部分的方差,![]() 是强度因子,用来控制水印的健壮程度和透明性。为了将方差降低到预期的级别,小波系数
是强度因子,用来控制水印的健壮程度和透明性。为了将方差降低到预期的级别,小波系数![]() 将用下式中的直方图映射函数迭代地进行修改:(本文引用文献3中的方法)
将用下式中的直方图映射函数迭代地进行修改:(本文引用文献3中的方法)
其中,![]() [1,∞];
[1,∞]; ![]() 转换为
转换为![]() ,它们两者的符号保持一致,此外,变换的变量的绝对值随Km的增加而减小。且在区域[0 ,1]之间随Km的减小而增大。
,它们两者的符号保持一致,此外,变换的变量的绝对值随Km的增加而减小。且在区域[0 ,1]之间随Km的减小而增大。
所有在每个bin中的,变换后的小波系数将被映射到原始的范围中。然后进行时间的逆小波变换,同时,所有的序列平移到原始的重心处,得到嵌入水印的3-D序列。
水印嵌入过程图如下
水印提取:
本文中的水印算法提取过程相当简单。与水印嵌入过程相似,我们首先计算每个bin中的方差![]() 并两两进行比较。在第m个bin中嵌入的水印将按照下式进行提取:
并两两进行比较。在第m个bin中嵌入的水印将按照下式进行提取:
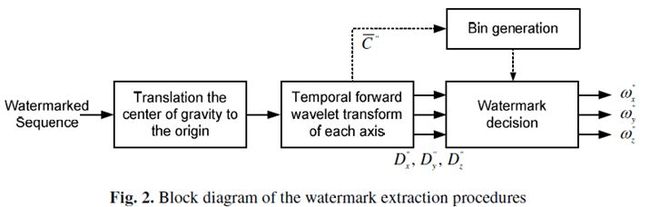
文中的水印提取不需要原始序列,因此是一种盲水印算法,水印提取图如下
总结:
论文提出的水印嵌入和提取方案大致如上所述,论文的其他篇幅主要用于实验验证。理解论文的难点在于如何将顶点划分到不同的bin中。总结起来说,作者先将序列分为高频部分和低频部分,然后求出低频部分的平均值,将这个平均值的笛卡尔坐标转换为球面坐标。球面坐标中有一个分量代表法向,根据大小,将法向分量的概率分布划分成M个独立等范围的bin,至此顶点被分到了不同的bin中,然后根据要嵌入的水印的值,对不同bin中的顶点的小波系数进行修改,以改变bin中顶点组的小波系数的方差。将进行了更改后的顶点坐标映射回笛卡尔坐标,并进行小波逆变换便得到了嵌入水印的序列。在提取时,直接计算每个bin的方差,比较正数部分方差和负数部分方差的大小便可提取出嵌入的水印。