- 20个新手学习c++必会的程序 输出*三角形、杨辉三角等(附代码)
X_StarX
c++学习算法大学生开发语言数据结构
示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
- 自学Python:计算斐波纳契数列
小强聊成长
斐波那契数列(Fibonaccisequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(LeonardodaFibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准
- 斐波纳契数列(f(n)=f(n-1)+f(n-2))问题
剑海风云
Algorithm算法数列
packageorg.nxt.algorithm.series;importjava.math.BigInteger;/***fibonacciseries*@authornanxiaotao**/publicclassFibonacciSeries{privatestaticBigInteger[][]matrix(BigInteger[][]arrLeft,BigInteger[][]arrR
- 搜索算法之斐波那契搜索详细解读(附带Java代码解读)
南城花随雪。
算法分析算法数据结构排序算法
斐波那契搜索(FibonacciSearch)详细介绍1.基本概念斐波那契搜索是一种高效的查找算法,用于在已排序的数组中查找目标值。它使用斐波那契数列来确定中间点,避免了二分搜索中的中点计算问题。斐波那契数列是由F(n)=F(n-1)+F(n-2)定义的,初始值为F(0)=0和F(1)=1。2.工作原理斐波那契搜索的基本步骤如下:初始化:计算斐波那契数列中适合当前数组长度的最大值F(k),其中F(
- 笔试强训day04
ao_lang
笔试强训算法图论深度优先
Fibonacci数列#includeusingnamespacestd;intn;intmain(){cin>>n;inta=0,b=1,c=1;while(n>c){a=b;b=c;c=a+b;}cout#includeclassSolution{private:intn,m;intdx[4]={1,-1,0,0},dy[4]={0,0,1,-1};boolvis[110][110]{};bo
- 斐波那契数列——C语言
木木ᶻ
c语言蓝桥杯算法
目录一、递归法二、for循环三、for循环+数组斐波那契数列(Fibonaccisequence),也称之为黄金分割数列,由意大利数学家列昂纳多・斐波那契(LeonardoFibonacci)提出。斐波那契数列指的是这样的一个数列:1、1、2、3、5、8、13、21、34、……,这个数列从第3项开始,每一项都等于前面两项之和。在数学上,斐波那契数列可以被递推的方法定义如下:F(1)=1F(2)=1
- Fibonacci Number
GakkiLove
GettheKthnumberintheFibonacciSequence.(Kis0-indexed,the0thFibonaccinumberis0andthe1stFibonaccinumberis1).Examples0thfibonaccinumberis01stfibonaccinumberis12ndfibonaccinumberis13rdfibonaccinumberis26th
- 博弈论笔记总结
Royen_
博弈论博弈论acm竞赛
博弈论一、四大博弈模型1.巴什博弈(BashGame)2.斐波那契博弈(FibonacciGame)3.威佐夫博弈(WythoffGame)4.尼姆博弈(NimGame)二、SG函数0.前言1.前置知识公平组合游戏(ICG游戏)必胜态与必败态DAG(有向无环图)中的博弈2.SG函数Mex运算定义性质SG定理解题方法参考资料一、四大博弈模型1.巴什博弈(BashGame)Problem一堆n个物品,
- [Algorithm][综合训练][数组中两个字符串的最小距离][Fibonacci数列][单词搜索]详细讲解
DieSnowK
[OJ]#[综合训练]算法Algorithm综合训练数组中两个字符串的最小距离Fibonacci数列单词搜索详细讲解
目录1.数组中两个字符串的最小距离1.题目链接2.算法原理详解&&代码实现2.Fibonacci数列1.题目链接2.算法原理详解&&代码实现3.单词搜索1.题目链接2.算法原理详解&&代码实现1.数组中两个字符串的最小距离1.题目链接数组中两个字符串的最小距离2.算法原理详解&&代码实现自己的版本:85%贪心错误原因:这样贪心只是一直在往后找两组可能的新的str来更新最小值,但是前面仍然有可能存在
- 【48天笔试强训】day7
革凡成圣211
算法数据结构
Fibonacci数列描述Fibonacci数列是这样定义的:F[0]=0F[1]=1foreachi≥2:F[i]=F[i-1]+F[i-2]因此,Fibonacci数列就形如:0,1,1,2,3,5,8,13,...,在Fibonacci数列中的数我们称为Fibonacci数。给你一个N,你想让其变为一个Fibonacci数,每一步你可以把当前数字X变为X-1或者X+1,现在给你一个数N求最少
- 前端面试题-笔试题
Alice_66
javascript前端
请实现一个fibonacci函数,要求实现以下功能斐波那契数列:[1,1,2,3,5,8,13,…]fibonacci(0)=>1fibonacci(6)=>8functionfibonacci(count){functionfn(count,cur=1,next=1){if(count===0){returncur}else{returnfn(count-1,next,cur+next)}}re
- MATLAB知识点:fibonacci函数(★☆☆☆☆)返回斐波那契数列
数学建模学习交流
MATLAB知识点详解matlab开发语言数学建模
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili节选自第3章:课后习题讲解中拓展的函数在讲解第三章课后习题的过程中,我给大家拓展了一些讲义中没有介绍的新函数:(4)fibonacci函数(★☆☆☆☆)fibonacci函数可返回斐波那契数列,该函数需要符号数学工具箱
- 剑指Offer:07-斐波那契数列
jackmxp
题目描述大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39思路实现1-递归classSolution{public:intFibonacci(intn){if(n<=1)returnn;returnFibonacci(n-1)+Fibonacci(n-2);}};实现2-非递归classSolution{public:intFibona
- C#,泰波拿契数(Tribonacci Number)的算法与源代码
深度混淆
C#算法演义AlgorithmRecipesc#算法泰波那契数TribonacciFibonacci
1泰波拿契数(TribonacciNumber)泰波拿契数(TribonacciNumber)是斐波那契的拓展。泰波拿契数(TribonacciNumber)即把费波拿契数(FibonacciNumber)的概念推广至三个数。2计算结果3源程序usingSystem;namespaceLegalsoft.Truffer.Algorithm{publicstaticpartialclassNumbe
- PTA 数组(C语言)
Anemia_
C语言c语言
文章目录1.选择法排序(20分)2.交换最小值和最大值(15分)3.fibonacci数列(10分)4.逆序(10分)5.插入有序数组(10分)6.找10个整数中的最大值(12分)7.找出数组中元素的最大数,并指出其位置(10分)8.排序问题(15分)9.计算字符串数组长度(10分)10.字符串字母大小写转换(15分)11.字符串连接(15分)12.将字符串逆序输出(15分)13.996(15分)
- PTA 循环结构设计(C语言)
Anemia_
C语言c语言
文章目录1.求交错序列前N项和(15分)2.统计素数并求和(20分)3.求分数序列前N项和(15分)4.猴子吃桃问题(15分)6.近似求PI(15分)6.最佳情侣身高差(10分)7.Fibonacci数列(16分)8.统计数字字符和空格(15分)9.数列求和(300分)10.C程序设计实验3-1(10分)11.实验3-2(10分)12.实验3-3(10分)13.for循环练习:输出1到X间所有数的
- C语言:用递归函数求Fibonacci数列
不吃橘子的橘猫
C语言作业c语言算法c++
#includeintfib(intn);intmain(){inti,n,f1;printf("InputFibonacci'snumber:");scanf("%d",&n);for(i=1;i<=n;i++){f1=fib(i);printf("%6d",f1);if(i%5==0)printf("\n");}printf("\n");}intfib(intn){intf;if(n==1||
- 动态一:斐波那契数
程一刀
题目地址:https://leetcode-cn.com/problems/fibonacci-number/题目描述:斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)示例1:输入:2输出:1解释:F(2)=F(1)+F(0
- 【水文】计算斐波那契数列的第n项
paid星!亦舒!
C
#include//函数声明intfibonacci(intn);intmain(){//输入正整数nintn;printf("请输入一个正整数n:");scanf("%d",&n);//调用函数计算斐波那契数列的第n项并输出结果intresult=fibonacci(n);printf("斐波那契数列的第%d项为:%d\n",n,result);return0;}//递归函数计算斐波那契数列的第
- 斐波那契数列--数组和递归的方式实现
钮轱辘噶
学习方法
请用数组和递归的方式分别实现计算斐波那契数列的第20项1、1、2、3、5、8、13、21、34,n=1和n=2的时候都是输出1公式:f(n)=f(n-1)+f(n-2);例如第20项,6765#include//数组intfibonacci1(intn){intfib[n+1];fib[1]=1;fib[2]=1;for(inti=3;i<=n;i++){fib[i]=fib[i-1]+fib[i
- offer10: 斐波拉契数列
Quintanliu
一、问题写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项(即F(N))。斐波那契数列的定义如下:F(0)=0,F(1)=1F(N)=F(N-1)+F(N-2),其中N>1.斐波那契数列由0和1开始,之后的斐波那契数就是由之前的两数相加而得出。答案需要取模1e9+7(1000000007),如计算初始结果为:1000000008,请返回1。示例1输入:n=2输出:1示例2输入:n=5
- 试题 入门训练 Fibonacci数列(C语言)
melody_yuan
资源限制时间限制:1.0s内存限制:256.0MB问题描述Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。输入格式输入包含一个整数n。输出格式输出一行,包含一个整数,表示Fn除以10007的余数。说明:在本题中,答案是要求Fn除以10007的余数,因此我们只要能算出这个余数即可,而不需要先
- 常用Fibonacci数性质
consult_
数学
常用Fibonacci数性质0.Fn−1+Fn−2=Fn,特殊的F0=1,F1=1上述式子为定义式1.F(0)+F(1)+…+F(n)=F(n+2)−1证明:F0+F1=F2F1+F2=F3F2+F3=F4⋮Fn+Fn+1=Fn+2F0+2F1+2F2+…+2Fn+Fn+1=F1+F2+…+Fn+2F0+F1+F2+…+Fn+Fn+1=Fn+2−F1=Fn+2−12.F(1)+F(3)+…+F(2
- 用动态规划、矩阵快速幂求解斐波那契数列
北辰2023
数据结构与算法设计动态规划矩阵算法
斐波那契数列(Fibonaccisequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(LeonardoFibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……在数学上,这一数列以如下递推的方法定义:F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)。本文将介绍Fibonacci数列的动态规划
- c语言递归函数头文件,C语言函数,递归,功能模块头文件(习题)
摘星的猪
c语言递归函数头文件
递归:直接或者间接调用自身函数1.返回值函数名(形参){...函数名(实参);...}注:1,when从什么时候2,when到什么时候结束3,what每次递归时你需要干嘛习题:斐波那契数列(Fibonaccisequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(LeonardodaFibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、
- 代码随想录算法训练营29期Day38|LeetCode 509,70,746
tlingyuqi
代码随想录算法训练营29期算法leetcodec++职场和发展动态规划
文档讲解:动态规划理论基础斐波那契数爬楼梯使用最小花费爬楼梯509.斐波那契数题目链接:https://leetcode.cn/problems/fibonacci-number/description/思路:当前这个数由上一个数和上上个数推导而来。所以我们每次记录两个数,用来推导下一个就行了。遍历顺序从2到n,当n小于等于2时可直接输出结果。核心代码:classSolution{public:i
- golang编程语言和java的性能对比
QFdongdong
这篇文章主要介绍了golang、java性能的对比,需要的朋友可以参考下!1、先说Go吧,因为我个人最近正在用,感觉很不错packagemainimport"fmt"funcmain(){fmt.Println(fibonacci(34))}funcfibonacci(iint)int{if(i<2){returni;}returnfibonacci(i-2)+fibonacci(i-1);}先用
- PYTHON蓝桥杯——每日一练(简单题)
詹小菜
蓝桥杯蓝桥杯python
题目Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。输入格式输入包含一个整数n。输出格式输出一行,包含一个整数,表示Fn除以10007的余数。解析一、int(input())获得n的数列二、设置数列的前俩项三、从点三项开始算起到n项,再用数列最后一项除以10007代码运行结果
- PTA 习题6-4 使用函数输出指定范围内的Fibonacci数 (20分)
eclipse_ali
PTAc语言
本题要求实现一个计算Fibonacci数的简单函数,并利用其实现另一个函数,输出两正整数m和n(0intfib(intn);voidPrintFN(intm,intn);intmain(){intm,n,t;scanf("%d%d%d",&m,&n,&t);printf("fib(%d)=%d\n",t,fib(t));PrintFN(m,n);return0;}/*你的代码将被嵌在这里*/输入样
- c语言--求第n个斐波那契数列(递归、迭代)
权^
c语言
目录一、概念二、用迭代求第n个斐波那契数1.分析2.完整代码3.运行结果4.如果求第50个斐波那契数呢?看看会怎么样。4.1运行结果:4.2画图解释三、用迭代的方式求第n个斐波那契数列1.分析2.完整代码3.运行结果4.求第50个斐波那契数4.1运行结果4.2运行结果的解释四、总结一、概念斐波那契数列(Fibonaccisequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonar
- Java序列化进阶篇
g21121
java序列化
1.transient
类一旦实现了Serializable 接口即被声明为可序列化,然而某些情况下并不是所有的属性都需要序列化,想要人为的去阻止这些属性被序列化,就需要用到transient 关键字。
- escape()、encodeURI()、encodeURIComponent()区别详解
aigo
JavaScriptWeb
原文:http://blog.sina.com.cn/s/blog_4586764e0101khi0.html
JavaScript中有三个可以对字符串编码的函数,分别是: escape,encodeURI,encodeURIComponent,相应3个解码函数:,decodeURI,decodeURIComponent 。
下面简单介绍一下它们的区别
1 escape()函
- ArcgisEngine实现对地图的放大、缩小和平移
Cb123456
添加矢量数据对地图的放大、缩小和平移Engine
ArcgisEngine实现对地图的放大、缩小和平移:
个人觉得是平移,不过网上的都是漫游,通俗的说就是把一个地图对象从一边拉到另一边而已。就看人说话吧.
具体实现:
一、引入命名空间
using ESRI.ArcGIS.Geometry;
using ESRI.ArcGIS.Controls;
二、代码实现.
- Java集合框架概述
天子之骄
Java集合框架概述
集合框架
集合框架可以理解为一个容器,该容器主要指映射(map)、集合(set)、数组(array)和列表(list)等抽象数据结构。
从本质上来说,Java集合框架的主要组成是用来操作对象的接口。不同接口描述不同的数据类型。
简单介绍:
Collection接口是最基本的接口,它定义了List和Set,List又定义了LinkLi
- 旗正4.0页面跳转传值问题
何必如此
javajsp
跳转和成功提示
a) 成功字段非空forward
成功字段非空forward,不会弹出成功字段,为jsp转发,页面能超链接传值,传输变量时需要拼接。接拼接方式list.jsp?test="+strweightUnit+"或list.jsp?test="+weightUnit+&qu
- 全网唯一:移动互联网服务器端开发课程
cocos2d-x小菜
web开发移动开发移动端开发移动互联程序员
移动互联网时代来了! App市场爆发式增长为Web开发程序员带来新一轮机遇,近两年新增创业者,几乎全部选择了移动互联网项目!传统互联网企业中超过98%的门户网站已经或者正在从单一的网站入口转向PC、手机、Pad、智能电视等多端全平台兼容体系。据统计,AppStore中超过85%的App项目都选择了PHP作为后端程
- Log4J通用配置|注意问题 笔记
7454103
DAOapachetomcatlog4jWeb
关于日志的等级 那些去 百度就知道了!
这几天 要搭个新框架 配置了 日志 记下来 !做个备忘!
#这里定义能显示到的最低级别,若定义到INFO级别,则看不到DEBUG级别的信息了~!
log4j.rootLogger=INFO,allLog
# DAO层 log记录到dao.log 控制台 和 总日志文件
log4j.logger.DAO=INFO,dao,C
- SQLServer TCP/IP 连接失败问题 ---SQL Server Configuration Manager
darkranger
sqlcwindowsSQL ServerXP
当你安装完之后,连接数据库的时候可能会发现你的TCP/IP 没有启动..
发现需要启动客户端协议 : TCP/IP
需要打开 SQL Server Configuration Manager...
却发现无法打开 SQL Server Configuration Manager..??
解决方法: C:\WINDOWS\system32目录搜索framedyn.
- [置顶] 做有中国特色的程序员
aijuans
程序员
从出版业说起 网络作品排到靠前的,都不会太难看,一般人不爱看某部作品也是因为不喜欢这个类型,而此人也不会全不喜欢这些网络作品。究其原因,是因为网络作品都是让人先白看的,看的好了才出了头。而纸质作品就不一定了,排行榜靠前的,有好作品,也有垃圾。 许多大牛都是写了博客,后来出了书。这些书也都不次,可能有人让为不好,是因为技术书不像小说,小说在读故事,技术书是在学知识或温习知识,有些技术书读得可
- document.domain 跨域问题
avords
document
document.domain用来得到当前网页的域名。比如在地址栏里输入:javascript:alert(document.domain); //www.315ta.com我们也可以给document.domain属性赋值,不过是有限制的,你只能赋成当前的域名或者基础域名。比如:javascript:alert(document.domain = "315ta.com");
- 关于管理软件的一些思考
houxinyou
管理
工作好多看年了,一直在做管理软件,不知道是我最开始做的时候产生了一些惯性的思维,还是现在接触的管理软件水平有所下降.换过好多年公司,越来越感觉现在的管理软件做的越来越乱.
在我看来,管理软件不论是以前的结构化编程,还是现在的面向对象编程,不管是CS模式,还是BS模式.模块的划分是很重要的.当然,模块的划分有很多种方式.我只是以我自己的划分方式来说一下.
做为管理软件,就像现在讲究MVC这
- NoSQL数据库之Redis数据库管理(String类型和hash类型)
bijian1013
redis数据库NoSQL
一.Redis的数据类型
1.String类型及操作
String是最简单的类型,一个key对应一个value,string类型是二进制安全的。Redis的string可以包含任何数据,比如jpg图片或者序列化的对象。
Set方法:设置key对应的值为string类型的value
- Tomcat 一些技巧
征客丶
javatomcatdos
以下操作都是在windows 环境下
一、Tomcat 启动时配置 JAVA_HOME
在 tomcat 安装目录,bin 文件夹下的 catalina.bat 或 setclasspath.bat 中添加
set JAVA_HOME=JAVA 安装目录
set JRE_HOME=JAVA 安装目录/jre
即可;
二、查看Tomcat 版本
在 tomcat 安装目
- 【Spark七十二】Spark的日志配置
bit1129
spark
在测试Spark Streaming时,大量的日志显示到控制台,影响了Spark Streaming程序代码的输出结果的查看(代码中通过println将输出打印到控制台上),可以通过修改Spark的日志配置的方式,不让Spark Streaming把它的日志显示在console
在Spark的conf目录下,把log4j.properties.template修改为log4j.p
- Haskell版冒泡排序
bookjovi
冒泡排序haskell
面试的时候问的比较多的算法题要么是binary search,要么是冒泡排序,真的不想用写C写冒泡排序了,贴上个Haskell版的,思维简单,代码简单,下次谁要是再要我用C写冒泡排序,直接上个haskell版的,让他自己去理解吧。
sort [] = []
sort [x] = [x]
sort (x:x1:xs)
| x>x1 = x1:so
- java 路径 配置文件读取
bro_feng
java
这几天做一个项目,关于路径做如下笔记,有需要供参考。
取工程内的文件,一般都要用相对路径,这个自然不用多说。
在src统计目录建配置文件目录res,在res中放入配置文件。
读取文件使用方式:
1. MyTest.class.getResourceAsStream("/res/xx.properties")
2. properties.load(MyTest.
- 读《研磨设计模式》-代码笔记-简单工厂模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* 个人理解:简单工厂模式就是IOC;
* 客户端要用到某一对象,本来是由客户创建的,现在改成由工厂创建,客户直接取就好了
*/
interface IProduct {
- SVN与JIRA的关联
chenyu19891124
SVN
SVN与JIRA的关联一直都没能装成功,今天凝聚心思花了一天时间整合好了。下面是自己整理的步骤:
一、搭建好SVN环境,尤其是要把SVN的服务注册成系统服务
二、装好JIRA,自己用是jira-4.3.4破解版
三、下载SVN与JIRA的插件并解压,然后拷贝插件包下lib包里的三个jar,放到Atlassian\JIRA 4.3.4\atlassian-jira\WEB-INF\lib下,再
- JWFDv0.96 最新设计思路
comsci
数据结构算法工作企业应用公告
随着工作流技术的发展,工作流产品的应用范围也不断的在扩展,开始进入了像金融行业(我已经看到国有四大商业银行的工作流产品招标公告了),实时生产控制和其它比较重要的工程领域,而
- vi 保存复制内容格式粘贴
daizj
vi粘贴复制保存原格式不变形
vi是linux中非常好用的文本编辑工具,功能强大无比,但对于复制带有缩进格式的内容时,粘贴的时候内容错位很严重,不会按照复制时的格式排版,vi能不能在粘贴时,按复制进的格式进行粘贴呢? 答案是肯定的,vi有一个很强大的命令可以实现此功能 。
在命令模式输入:set paste,则进入paste模式,这样再进行粘贴时
- shell脚本运行时报错误:/bin/bash^M: bad interpreter 的解决办法
dongwei_6688
shell脚本
出现原因:windows上写的脚本,直接拷贝到linux系统上运行由于格式不兼容导致
解决办法:
1. 比如文件名为myshell.sh,vim myshell.sh
2. 执行vim中的命令 : set ff?查看文件格式,如果显示fileformat=dos,证明文件格式有问题
3. 执行vim中的命令 :set fileformat=unix 将文件格式改过来就可以了,然后:w
- 高一上学期难记忆单词
dcj3sjt126com
wordenglish
honest 诚实的;正直的
argue 争论
classical 古典的
hammer 锤子
share 分享;共有
sorrow 悲哀;悲痛
adventure 冒险
error 错误;差错
closet 壁橱;储藏室
pronounce 发音;宣告
repeat 重做;重复
majority 大多数;大半
native 本国的,本地的,本国
- hibernate查询返回DTO对象,DTO封装了多个pojo对象的属性
frankco
POJOhibernate查询DTO
DTO-数据传输对象;pojo-最纯粹的java对象与数据库中的表一一对应。
简单讲:DTO起到业务数据的传递作用,pojo则与持久层数据库打交道。
有时候我们需要查询返回DTO对象,因为DTO
- Partition List
hcx2013
partition
Given a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.
You should preserve the original relative order of th
- Spring MVC测试框架详解——客户端测试
jinnianshilongnian
上一篇《Spring MVC测试框架详解——服务端测试》已经介绍了服务端测试,接下来再看看如果测试Rest客户端,对于客户端测试以前经常使用的方法是启动一个内嵌的jetty/tomcat容器,然后发送真实的请求到相应的控制器;这种方式的缺点就是速度慢;自Spring 3.2开始提供了对RestTemplate的模拟服务器测试方式,也就是说使用RestTemplate测试时无须启动服务器,而是模拟一
- 关于推荐个人观点
liyonghui160com
推荐系统关于推荐个人观点
回想起来,我也做推荐了3年多了,最近公司做了调整招聘了很多算法工程师,以为需要多么高大上的算法才能搭建起来的,从实践中走过来,我只想说【不是这样的】
第一次接触推荐系统是在四年前入职的时候,那时候,机器学习和大数据都是没有的概念,什么大数据处理开源软件根本不存在,我们用多台计算机web程序记录用户行为,用.net的w
- 不间断旋转的动画
pangyulei
动画
CABasicAnimation* rotationAnimation;
rotationAnimation = [CABasicAnimation animationWithKeyPath:@"transform.rotation.z"];
rotationAnimation.toValue = [NSNumber numberWithFloat: M
- 自定义annotation
sha1064616837
javaenumannotationreflect
对象有的属性在页面上可编辑,有的属性在页面只可读,以前都是我们在页面上写死的,时间一久有时候会混乱,此处通过自定义annotation在类属性中定义。越来越发现Java的Annotation真心很强大,可以帮我们省去很多代码,让代码看上去简洁。
下面这个例子 主要用到了
1.自定义annotation:@interface,以及几个配合着自定义注解使用的几个注解
2.简单的反射
3.枚举
- Spring 源码
up2pu
spring
1.Spring源代码
https://github.com/SpringSource/spring-framework/branches/3.2.x
注:兼容svn检出
2.运行脚本
import-into-eclipse.bat
注:需要设置JAVA_HOME为jdk 1.7
build.gradle
compileJava {
sourceCompatibilit
- 利用word分词来计算文本相似度
yangshangchuan
wordword分词文本相似度余弦相似度简单共有词
word分词提供了多种文本相似度计算方式:
方式一:余弦相似度,通过计算两个向量的夹角余弦值来评估他们的相似度
实现类:org.apdplat.word.analysis.CosineTextSimilarity
用法如下:
String text1 = "我爱购物";
String text2 = "我爱读书";
String text3 =
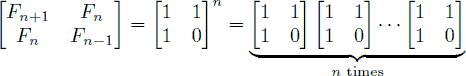 .
. .
.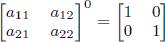 .
.