LSH的基本原理
1:LocalitySensitive Hashing
LocalitySensitive Hashing 是构造一种Hash函数集{g| Rd->U}其中d是点的维数,使得对任意的点p,q有:
——if||p-q|| <= r, then Pr[g(p)=g(q)] 要很高
——If ||p-q|| >cr, then Pr[g(p)=g(q)]要很低
如下图:
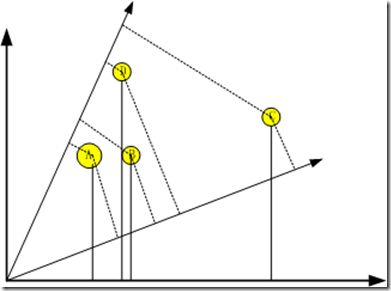
2:基于投影的LSH原理
如下图:
理如图:A(xa, ya), B(xb, yb), C(xc, yc), D(xd, yd);如果取的Hash函数为 H(A(xa, ya))= xa(即在X轴上的投影);那么就有A,B,C,D在X轴上的投影分别是:xa,xb,xc, xd重点来了,空间相近的点在X轴上的投影也是相近的,这样我们可以利用这个特性来做临近点的查询,基于投影的LSH的基本原理就是这样的。
不过上面这种方法是能能保证挨得近的点hash后得到的一维值也挨的很近,但是一些本来不近的点在hash后,得到的也是很近的值,如A与D点。
3:(P1,P2,r,cr)-sensitive LSH的定义
A family H of functions h: Rd → U is called (P1,P2,r,cr)-sensitive, if for any p,q:
– if ||p-q|| <r then Pr[ h(p)=h(q) ] > P1
– if ||p-q|| >cr then Pr[ h(p)=h(q) ] < P2
第2部分的构造的H(A(xa, ya))= xa(即在X轴上的投影)是不能满足这个要求的,
解决的办法是:
如图,基本想法也是很简单的,就是在空间多做几条线,这样本来很久的点,无论在哪条线上的映射都是很近的,而挨的不近点可能在某个方向的的投影很近,但在其它方向就可能很远,这样,把每个方向的投影结果都利用(可以对这些结果在进行hash
现在的问题是:空间线怎么取?到底要取多少条这样的线?
空间的线怎样取,在E2LSH中,是根据标准正态分布取的,为什么这呢?我觉得是便于理论证明 可以满足(P1,P2,r,cr)-sensitive LSH的定义。至于怎样证明还是需要看看作者的论文和相关文档。