再生核希尔伯特空间(RKHS)在监督学习(SVM)中的应用
【转载请注明出处】http://www.cnblogs.com/mashiqi
2014/4/10
在网上找到一个讲reproducing kernel的tutorial看了一看,下面介绍一下。
首先定义kernel(核) :
:
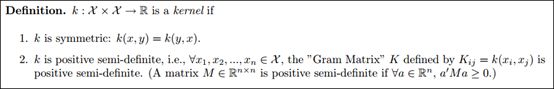
于是我们可以从一个空间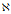 定义出一个kernel。接着,我们使用一个kernel来定义一个从
定义出一个kernel。接着,我们使用一个kernel来定义一个从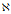 到的
到的 映射
映射 ,并称这个映射为reproducing kernel feature map(再生核特征映射):
,并称这个映射为reproducing kernel feature map(再生核特征映射):
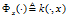 .
.
这个映射的意思是:特定的kernel 和
和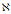 上的一个特定的元素
上的一个特定的元素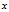 构成了一个映射规则,将
构成了一个映射规则,将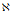 的任意元素
的任意元素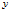 的映射成一个实数
的映射成一个实数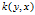 ,那么,实际上,
,那么,实际上, 就是将
就是将 映射成了
映射成了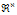 。
。
值得注意的是,在泛函分析 中,Hilbert空间上的"
中,Hilbert空间上的" 表现定理"说的是,任意一个内积
表现定理"说的是,任意一个内积 都可以等价于一个线性泛函,任意一个线性泛函也等价于某个内积
都可以等价于一个线性泛函,任意一个线性泛函也等价于某个内积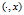 ,即对任意线性泛函
,即对任意线性泛函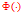 ,
, ,使得
,使得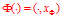 。然而这里的"再生核特征映射"和"线性泛函"的区别是:
。然而这里的"再生核特征映射"和"线性泛函"的区别是:
再生核特征映射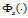 是由某个核
是由某个核 生成的;
生成的;
而线性泛函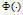 是由内积
是由内积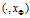 生成的。
生成的。
下面我们通过这个映射来定义一个Hilbert space。
第一步,构造一个空间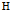 (现在它还不完备,稍后会将它完备化)。于是
(现在它还不完备,稍后会将它完备化)。于是 ,将
,将 所张成的空间记为
所张成的空间记为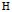 :
:
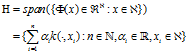
第二步,在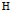 上定义内积:
上定义内积:
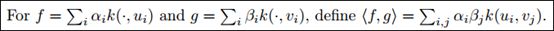
于是我们可以很容易的验证此内积满足内积的三个条件。
第三步,将空间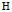 完备化。
完备化。
于是我们就由kernel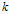 构造出一个完备的希尔伯特空间,此空间称为reproducing kernel Hilbert space(再生核希尔伯特空间):
构造出一个完备的希尔伯特空间,此空间称为reproducing kernel Hilbert space(再生核希尔伯特空间):

在第二步定义内积的过程中,我们可以发现,对于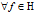 ,有
,有

我们称满足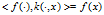 的
的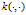 为reproducing kernel(再生核)。
为reproducing kernel(再生核)。
Reference
[1] http://www.cs.berkeley.edu/~bartlett/courses/281b-sp08/7.pdf
2014/4/19
今天接着10号继续看再生核空间的内容。
今天终于有了些进展,下面讲讲这个再生核到底是怎么回事。
首先我们有一个由泛函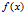 构成的空间:
构成的空间:

这些泛函又是定义在集合 上的。通常,我们的思路一般会把
上的。通常,我们的思路一般会把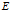 默认为Hilbert空间,然后将
默认为Hilbert空间,然后将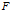 理解为它的对偶空间。我最开始就是这样默认的。但是其实这里不应该这样去理解它。再生核理论基本上了默认以空间
理解为它的对偶空间。我最开始就是这样默认的。但是其实这里不应该这样去理解它。再生核理论基本上了默认以空间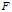 为Hilbert空间的,而集合
为Hilbert空间的,而集合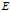 只是理解为一个一般的集合。然后,再生核
只是理解为一个一般的集合。然后,再生核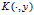 也是
也是 内的一个元,只是他相比较于一般的元
内的一个元,只是他相比较于一般的元 而言,拥有更多的性质。好,大概铺垫完了,下面给出一些具体的定义,大部分内容来自
而言,拥有更多的性质。好,大概铺垫完了,下面给出一些具体的定义,大部分内容来自 。
。
我们首先来给出reproducing Kernel(r.k.再生核)的定义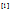 :
:

也就是说,现在我们有一个Hilbert空间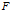 ,Hilbert空间
,Hilbert空间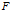 里面的每一个点都是一个泛函:
里面的每一个点都是一个泛函:
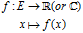
而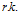
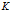 也是一个泛函
也是一个泛函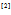 :
:
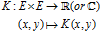
并且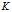 还必须满足两条性质:
还必须满足两条性质:
1、对于一个固定的 ,
, 是Hilbert空间
是Hilbert空间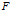 中的一个元素;
中的一个元素;
2、再生性质:对于每个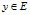 和
和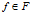 ,都有:
,都有:
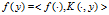
其中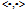 表示Hilbert空间
表示Hilbert空间 上的内积运算。根据这个再生性质,我们立即可以得到:
上的内积运算。根据这个再生性质,我们立即可以得到:

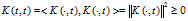
值得注意的是,式是一个令人满意的结果,根据这个式子我们可以很容易的得到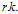 的正定性。根据这个再生性质,我们立即可以得到以下几个推论(直接截图了):
的正定性。根据这个再生性质,我们立即可以得到以下几个推论(直接截图了):
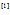 如果存在则唯一(
如果存在则唯一(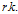 表示reproducing kernel):
表示reproducing kernel):
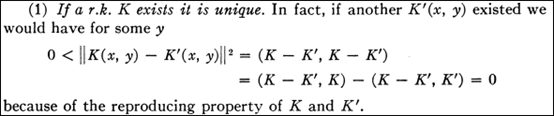
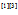 "存在再生核"等价于"每个泛函
"存在再生核"等价于"每个泛函 都连续":
都连续":

(*注:这里的连续性是指的 上的泛函
上的泛函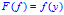 关于
关于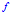 连续,而不是指的
连续,而不是指的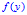 关于
关于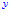 连续)
连续)
证明:
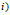 记
记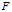 上的泛函
上的泛函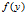 为
为 ,当
,当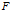 上存在kernel
上存在kernel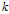
 时,有:
时,有:
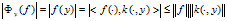
而根据式我们有:
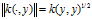
所以:

其中 和
和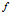 无关。所以
无关。所以 是有界泛函。又因为
是有界泛函。又因为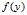 显然是线性的,所以
显然是线性的,所以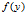 是连续泛函。
是连续泛函。
 而当
而当 是连续泛函时,因为它是线性的,所以根据
是连续泛函时,因为它是线性的,所以根据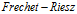 表现定理即可证明。
表现定理即可证明。
证毕。
这也正如 中所说:
中所说:

 再生核的正定性:
再生核的正定性:

正定性证明:
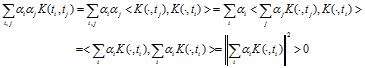
证毕。
(*注:正定性是指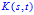 在集合
在集合 上的正定性,
上的正定性,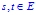 )
)
 还有一些其他性质,除了"命题8"以外,其他命题对于本次学习的目标并不是很重要:
还有一些其他性质,除了"命题8"以外,其他命题对于本次学习的目标并不是很重要:

接着我们要做的事就是构造这样一个Hilbert空间 ,这个空间上的内积
,这个空间上的内积 ,以及这个空间上的唯一的一个kernel
,以及这个空间上的唯一的一个kernel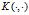 。
。
Reference
[1] Aronszajn, Nachman. "Theory of reproducing kernels." Transactions of the American mathematical society (1950): 337-404.
[2] 王敏慧,"几类高斯过程的Karhunen-Loève展开及再生核希尔伯特空间"[D],哈尔滨工业大学,2010
[3]Aronsazjn, Par N. "La théorie des noyaux reproduisants et ses applications Première Partie." Mathematical Proceedings of Cambridge Philosophical Society.Vol. 39. No. 03. Cambridge University Press, 1943.
[4] http://www.cs.berkeley.edu/~bartlett/courses/281b-sp08/7.pdf
2014/4/20
今天希望了解到上面所讲的关于RKHS的性质与我们SVM中(以及其他机器学习技术)的核技术的联系。
我们接着看 的5.1.3的定理1:
的5.1.3的定理1:

上面的逻辑可以这样描绘(这个图是重点):
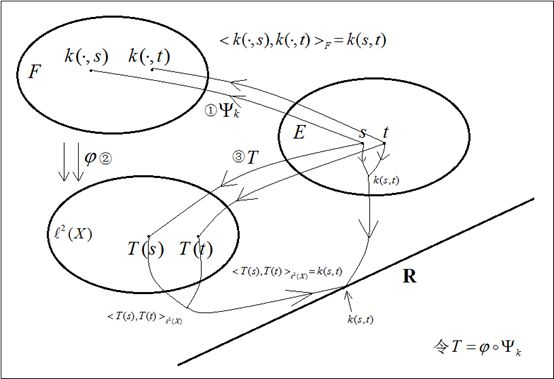
上图分别存在三个集合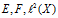 ,分别表示集合
,分别表示集合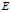 ,RKHS
,RKHS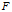 ,和我们所需要的空间
,和我们所需要的空间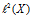 。分别存在三个映射①②③,分别表示
。分别存在三个映射①②③,分别表示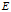 到
到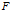 的映射
的映射 ,
,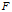 到
到 的映射
的映射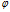 ,和
,和 到
到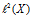 之间的映射
之间的映射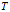 ,当
,当 的维数至多可数时,
的维数至多可数时,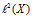 就是
就是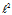 空间。首先讲解映射①,因为存在关系式:
空间。首先讲解映射①,因为存在关系式:
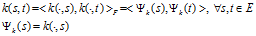
所以存在映射 ,使得:
,使得:

。又因为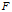 与
与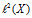 都是Hilbert空间,所以同构,所以存在同构映射
都是Hilbert空间,所以同构,所以存在同构映射 ,使得:
,使得:

那么,有了这两步的铺垫(映射①与映射②),我们便可以借助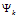 和
和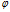 搭建
搭建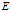 到
到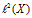 之间的映射
之间的映射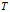 。结合两式,我们得到:
。结合两式,我们得到:
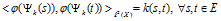
记新的复合映射为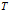 :
:
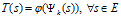
便得到了:
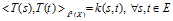
我们应该注意的是,虽然最后的式并没有涉及到Hilbert空间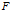 ,但是如果没有空间
,但是如果没有空间 在其中牵线搭桥,引出两个映射
在其中牵线搭桥,引出两个映射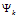 和
和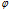 ,那我们也不可能找到映射
,那我们也不可能找到映射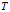 使得式得意满足。数学中的许多抽象概念在一些工程应用中虽不直接体现,但却给这些工程应用搭建了一些桥梁,使得工作可以继续深入!
使得式得意满足。数学中的许多抽象概念在一些工程应用中虽不直接体现,但却给这些工程应用搭建了一些桥梁,使得工作可以继续深入!
Reference
[1] Aronszajn, Nachman. "Theory of reproducing kernels." Transactions of the American mathematical society (1950): 337-404.
[2] 王敏慧,"几类高斯过程的Karhunen-Loève展开及再生核希尔伯特空间"[D],哈尔滨工业大学,2010