二叉树详解-第二篇 大根堆小根堆的实现,堆排序(源码讲解)
目录
1.堆的概念及结构
2.堆的性质:
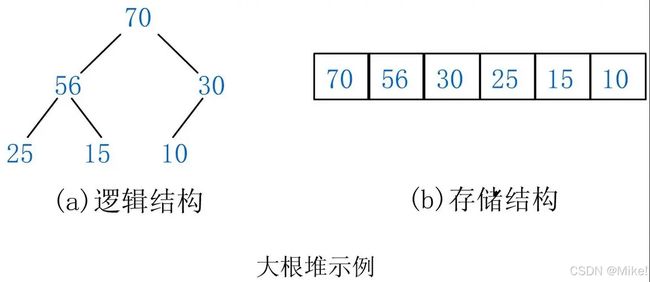
2.1大堆
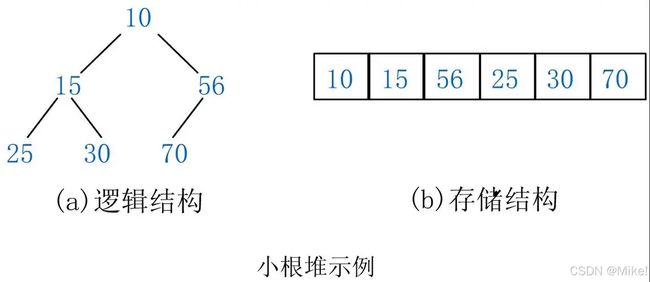
2.2小堆
3.堆的实现
3.1Heap.h源码
3.1.1Heap.h讲解
1.堆的结构体
3.2Heap.cpp源码
3.2.1Heap.cpp讲解
1.初始化函数 void Hpinit(HP* hp)
2.销毁函数 void Hpdestory(HP* hp)
3.插入函数 void Hppush(HP* hp, HeapType x)
4.向上调整算法 void adjustup(HeapType* a, int child)
5.向下调整算法 void adjustdown(HeapType*a,int size,int parent)
6.弹出堆顶元素 void Hppop(HP* hp)
7.返回堆顶元素值 HeapType HpTop(HP* hp)
8.判断堆是否为空 bool Hpempty(HP* hp)
3.3堆排序(堆排序是对数组排序,要与堆分清楚,堆只是打印有序,但是数组不是有序的)
void heapsort(HeapType *a,int n)// 对数组排序
3.4小根堆和大根堆的区别
1.向上调整算法 void adjustup(HeapType* a, int child) 的不同
1.1小根堆:
1.2大根堆:
2.向下调整算法 void adjustdown(HeapType*a,int size,int parent) 的不同
2.1小根堆:
2.2大根堆:
1.堆的概念及结构
堆是完全二叉树,将根节点最大的堆叫做最大堆或者大根堆,根节点最小的堆叫做最小堆或者小根堆。
2.堆的性质:
2.1大堆
1.是一个完全二叉树
2.任何一个父亲都>=孩子
特点:根是最大的
2.2小堆
1.是一个完全二叉树
2.任何一个父亲都<=孩子
特点:根是最小的
3.堆的实现
3.1Heap.h源码
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include
#include
#include
using namespace std;
typedef int HeapType;
typedef struct Heap
{
HeapType* a;
int size;
int cap;
}HP;
void Hpinit(HP* hp);
void Hpdestory(HP* hp);
void Hppush(HP* hp, HeapType x);
void Hppop(HP* hp);
void adjustup(HeapType* a, int child);;
void adjustdown(HeapType* a, int size, int parent);
HeapType HpTop(HP* hp);
bool Hpempty(HP* hp);
void heapsort(HeapType* a, int n);
3.1.1Heap.h讲解
1.堆的结构体
typedef int HeapType;
typedef struct Heap
{
HeapType* a;
int size;
int cap;
}HP;重命名变量类型为HeapType
结构体Heap中,a为动态顺序表,因为堆为完全二叉树,所以使用顺序存储结构,用下标来表示父子关系。size为当前堆中的元素个数,cap为堆的容量。
3.2Heap.cpp源码
#include"Heap.h"
void Hpinit(HP* hp)
{
assert(hp);
hp->a = NULL;
hp->cap = hp->size = 0;
}
void Hpdestory(HP* hp)
{
assert(hp);
hp->a = NULL;
hp->cap = hp->size = 0;
}
void Hppush(HP* hp, HeapType x)//要用到向上调整算法 小根堆把小的向上调整,大根堆把大的向上调整
{
assert(hp);
if (hp->size == hp->cap) {
int newcap = hp->cap == 0 ? 4 : hp->cap * 2;
HeapType* temp = (HeapType*)realloc(hp->a, newcap * sizeof(HeapType));
if (temp == NULL) {
perror("realloc");
return;
}
hp->a = temp;
hp->cap = newcap;
}
hp->a[hp->size++] = x;
adjustup(hp->a, hp->size - 1);
}
void Hppop(HP* hp)//删除堆顶数据,删除数组中第一个元素,但是不能直接删除第一个元素,因为后面的父子关系会乱
{
assert(hp->a);
assert(hp->size);
swap(hp->a[0], hp->a[hp->size - 1]);
hp->size--;
adjustdown(hp->a,hp->size, 0);
}
void adjustup(HeapType* a, int child) //从某个孩子的位置向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent]) {
swap(a[child], a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjustdown(HeapType*a,int size,int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child+1 a[child + 1])
{
child++;
}
if (a[parent] > a[child]) {
swap(a[parent], a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
HeapType HpTop(HP* hp)
{
assert(hp);
assert(hp->size > 0);
return hp->a[0];
}
bool Hpempty(HP* hp)
{
assert(hp);
return hp->size == 0;
}
void heapsort(HeapType *a,int n)// 对数组排序
{
//升序建立大堆
//降序建立小堆
for (int i = 1; i <= n; i++)
{
adjustup(a, i);//把一个数组建堆
}
int end = n - 1;
while (end)
{
swap(a[0], a[end]);
adjustdown(a, end, 0);
end--;
}
} 3.2.1Heap.cpp讲解
1.初始化函数 void Hpinit(HP* hp)
void Hpinit(HP* hp)
{
assert(hp);
hp->a = NULL;
hp->cap = hp->size = 0;
}用于对堆的初始化,将动态顺序表先赋为NULL指针,避免出现野指针,同时将size和cap都赋值为0。
2.销毁函数 void Hpdestory(HP* hp)
void Hpdestory(HP* hp)
{
assert(hp);
hp->a = NULL;
hp->cap = hp->size = 0;
}与初始化函数相同。
3.插入函数 void Hppush(HP* hp, HeapType x)
void Hppush(HP* hp, HeapType x)//要用到向上调整算法 小根堆把小的向上调整,大根堆把大的向上调整
{
assert(hp);
if (hp->size == hp->cap) {
int newcap = hp->cap == 0 ? 4 : hp->cap * 2;
HeapType* temp = (HeapType*)realloc(hp->a, newcap * sizeof(HeapType));
if (temp == NULL) {
perror("realloc");
return;
}
hp->a = temp;
hp->cap = newcap;
}
hp->a[hp->size++] = x;
adjustup(hp->a, hp->size - 1);
}
1.首先判断堆(*hp)是否为一个空指针。
2.在判断扩容,如果size==cap时,就要进行扩容,对动态顺序表扩容。
3.由于堆是由顺序表实现的,所以直接在顺序表最后加上要加入的元素即可。
4.加入元素后,要进行向上调整算法,要进行建队,如果建立小堆,就要把小的向上移动,如果建立大堆,就要把大的向上移动。详细请看对adjustup()的讲解。
4.向上调整算法 void adjustup(HeapType* a, int child)
void adjustup(HeapType* a, int child) //从某个孩子的位置向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent]) {
swap(a[child], a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}1.我们在第二叉树详解第一篇中讲到,孩子的父亲节点下标为(child - 1) / 2,所以我们求出父亲节点下标,以child>0为循环条件,因为child不能等于0,只需要到1即可。
2.然后判断儿子和父亲的值大小,如果儿子小于父亲就交换(建立小堆),(如果要建立大堆,就要改为当儿子大于父亲时就交换),如果儿子大于等于就退出循环。
5.向下调整算法 void adjustdown(HeapType*a,int size,int parent)
void adjustdown(HeapType*a,int size,int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child+1 a[child + 1])
{
child++;
}
if (a[parent] > a[child]) {
swap(a[parent], a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
} 1.向下调整算法用于删除元素时,当将第一个元素与最后一个元素交换后,我们要重新建堆,就要把第一个元素向下调整。
2.选儿子首先使用假设法,由于一个父亲有两个儿子,所以我们先选择第一个儿子(parent * 2 + 1),然后再让这个儿子与另一个儿子(child + 1)相比,如果建立小堆,就要选择一个最小的,也就是说如果a[child] > a[child + 1],就要将当前child加1,否则的话(a[child] <= a[child + 1])就不需要加1。(如果建立大堆就要选择一个最大的,也就是说a[child] < a[child + 1],就要将当前child加1)
3.选好儿子后,再判断a[parent] > a[child]是否为真,真就要交换,把最小的儿子换到parent的位置,将parent调整下来。如果为否直接退出循环。
6.弹出堆顶元素 void Hppop(HP* hp)
void Hppop(HP* hp)//删除堆顶数据,删除数组中第一个元素,但是不能直接删除第一个元素,因为后面的父子关系会乱
{
assert(hp->a);
assert(hp->size);
swap(hp->a[0], hp->a[hp->size - 1]);
hp->size--;
adjustdown(hp->a,hp->size, 0);
}1.弹出堆顶元素不能直接将第一个元素删除,这样会导致关系混乱,正确做法为交换第一个元素和最后一个元素,然后再将size--。然后以一个元素进行向下调整算法。
7.返回堆顶元素值 HeapType HpTop(HP* hp)
HeapType HpTop(HP* hp)
{
assert(hp);
assert(hp->size > 0);
return hp->a[0];
}1.直接返回顺序表第一个元素即可。
8.判断堆是否为空 bool Hpempty(HP* hp)
bool Hpempty(HP* hp)
{
assert(hp);
return hp->size == 0;
}1.返回hp->size == 0即可。
3.3堆排序(堆排序是对数组排序,要与堆分清楚,堆只是打印有序,但是数组不是有序的)
void heapsort(HeapType *a,int n)// 对数组排序
升序建立大堆
降序建立小堆
void heapsort(HeapType *a,int n)// 对数组排序
{
//升序建立大堆
//降序建立小堆
for (int i = 1; i <= n; i++)
{
adjustup(a, i);//把一个数组建堆
}
int end = n - 1;
while (end)
{
swap(a[0], a[end]);
adjustdown(a, end, 0);
end--;
}
}1.升序建大堆是因为,堆的第一个元素是最大值,我们只需把第一个元素与最后一个元素交换,这样就把最大的放到数组的最后面,再进行向下调整算法建堆,以此类推,随后就形成了一个升序。
2.降序建小堆是因为,堆的第一个元素是最小值,我们只需把第一个元素与最后一个元素交换,这样就把最小的放到数组的最后面,再进行向下调整算法建堆,以此类推,随后就形成了一个降序。
3.首先要把要排序的数组建队,使用向下调整算法对每个数组里的元素挨个使用,即可建堆。
4.使用一个end变量赋值为n-1,然后以end>0为条件,交换第一个元素和最后一个元素,然后向下调整算法,再end--。
3.4小根堆和大根堆的区别
1.向上调整算法 void adjustup(HeapType* a, int child) 的不同
1.1小根堆:
void adjustup(HeapType* a, int child) //从某个孩子的位置向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent]) {
swap(a[child], a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
由于是建立小根堆,所以if (a[child] < a[parent]),孩子比父亲小,孩子就要向上调整。
1.2大根堆:
void adjustup(HeapType* a, int child) //从某个孩子的位置向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent]) {
swap(a[child], a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
由于是建立小根堆,所以if (a[child] > a[parent]),孩子比父亲大,孩子就要向上调整。
2.向下调整算法 void adjustdown(HeapType*a,int size,int parent) 的不同
2.1小根堆:
void adjustdown(HeapType*a,int size,int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child+1 a[child + 1])
{
child++;
}
if (a[parent] > a[child]) {
swap(a[parent], a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
由于是建立小根堆,所以要在两个孩子之间选择一个最小的,所以if (child+1
a[child + 1]),并且当父亲比最小的孩子大时,把父亲向下调整。
2.2大根堆:
void adjustdown(HeapType*a,int size,int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child+1由于是建立大根堆,所以要在两个孩子之间选择一个最大的,所以if (child+1
本篇完