机械臂导纳控制公式

一 间接力控 Indirect Force Control

处理机械臂的末端执行器与环境之间相互作用问题。
约定：

定义	描述
${\Sigma }_e$	末端执行器坐标系
$p_e$	相对于坐标系e原点的位置矢量
$R_e$	相对于坐标系e的旋转矩阵
$v_e=({\dot{p}}_e^T{w}_e^T{)}^T$	末端执行器的刚体广义速度/运动旋量
${\dot{p}}_e$	位移矢量的倒数，即速度
$w_e$	角速度
$\dot{q}$	关节角速度
$J$	末端执行器几何雅克比矩阵
$v_e=J(q)\dot{q}$	速度与关节角速度的线性映射
$h_e=(f_e^T{m}_e^T{)}^T$	力旋量（wrench）：由作用在末端执行器上的力$f$和力矩$m$组成

$v_e=({\dot{p}}_e^T{w}_e^T{)}^T$表达方式的作用或者意义？ 定义一个向量$x=(x_1,x_2,x_3{)}^T\in {\mathbb{R}}^3$，那么我们有如下定义 [ x ] = [ 0 − x 3 x 2 x 3 0 − x 1 − x 2 x 1 0 ] ∈ S O ( 3 ) [x]=\left[ \begin{matrix} 0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{matrix} \right] \in SO(3) [x]= ​0x3​−x2​​−x3​0x1​​x2​−x1​0​ ​∈SO(3) $[x]$称为$x$的反对称矩阵(skew-symmetric matrix)。 反对称矩阵的主要性质为
$$[x]=-[x{]}^T$$
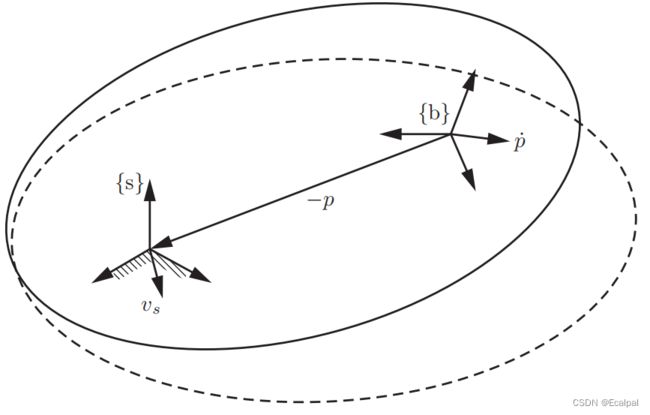
反对称矩阵在刚体角速度描述中的体现：该文1.7节

我们现在考虑运动坐标系的线速度和角速度。$s$和$b$分别表示固定(space)坐标系和移动(body)坐标系帧。齐次坐标变换为
$$T_{sb}(t)=T(t)=\left[\begin{array}{cc}R(t)& p(t)\\ 0& 1\end{array}\right]$$ 根据反对称矩阵的性质,对于旋转矩阵$R$有 $$S=\dot{R}{R}^{-1}$$ $S$这里的反对称矩阵在刚体运动中通常称为角速度矩阵。 同样的对于$T$也有如下性质 $$T^{-1}\dot{T}=\left[\begin{array}{cc}{R}^T& -R^{T}p\\ 0& 1\end{array}\right]\left[\begin{array}{cc}\dot{R}& \dot{p}\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}{R}^T\dot{R}& R^T\dot{p}\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}[w_b]& v_b\\ 0& 0\end{array}\right]$$ 分析上式可以观察得出一下结论
$R^T\dot{R}=[w_b]$是角速度矢量$w_b=(w_x,w_y,w_z{)}^T$在坐标系$b$中以反对称矩阵表示。
$R^T\dot{p}=v_b$是线速度矢量在坐标系$b$中的表示。 那么$[w_b]$和$v_b$就可以通过$T^{-1}\dot{T}$联系在一起描述和计算。 数学就是这么奇妙，角速度和线速度的联合也是后续动力学一些重要思想的基础，比如力旋量这个概念$wrench$.
对于运动坐标系$(body)$$b$,我们定义有$${\mathcal{V}}_b=\left[\begin{array}{c}{w}_b\\ v_b\end{array}\right]\in {\mathbb{R}}^6$$
可以称作spatial velocity in the body frame或者body twist 同理， $$T^{-1}\dot{T}=[{\mathcal{V}}_b]=\left[\begin{array}{cc}[w_b]& v_b\\ 0& 0\end{array}\right]\in SE(3)$$ 其中，$[w_b]\in SO(3),v_b\in {\mathbb{R}}^3$
至此，任何刚体运动都可以通过六个量来表示，即三个线速度和三个角速度，并且两者可以有联系地放在一起描述。

$$\dot{T}{T}^{-1}=\left[\begin{array}{cc}\dot{R}& \dot{p}\\ 0& 0\end{array}\right]\left[\begin{array}{cc}{R}^T& -R^{T}p\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}\dot{R}{R}^T& \dot{p}-\dot{R}{R}^{T}p\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}[w_s]& v_s\\ 0& 0\end{array}\right]$$
上式表示的是$s$坐标系下的速度与角速度，但这里的$v_s$不是直接对位移量$p$求导，因为$p$是相对于$v_b$而言的位移量，故
$$v_S=\dot{p}-\dot{R}{R}^{T}p=\dot{p}-w_s\times p=\dot{p}+w_s\times (-p)$$
反映的是运动物体上的点相对于静止坐标系的描述。 $${\mathcal{V}}_s=\left[\begin{array}{c}{w}_s\\ v_s\end{array}\right]\in {\mathbb{R}}^6$$ $$[{\mathcal{V}}_s]=\left[\begin{array}{cc}[w_s]& v_s\\ 0& 0\end{array}\right]\in SE(3)$$
可以称作spatial velocity in the space frame或者spatial twist
那么，可以推导出两个坐标系之间的运动旋量之间的转换关系
$$[{\mathcal{V}}_b]=T^{-1}\dot{T}=T^{-1}[{\mathcal{V}}_s]T$$
$$[{\mathcal{V}}_s]=T[{\mathcal{V}}_s]T^{-1}$$
展开$[{\mathcal{V}}_s]$可以得到
$$[{\mathcal{V}}_s]=\left[\begin{array}{cc}R[w_b]R^T& -R[w_b]R^{T}p+R{v}_b\\ 0& 0\end{array}\right]$$ 变形得到${\mathcal{V}}_s$和${\mathcal{V}}_b$之间的转换关系 $$\left[\begin{array}{c}{w}_s\\ v_s\end{array}\right]=\left[\begin{array}{cc}R& 0\\ [p]R& R\end{array}\right]\left[\begin{array}{c}{w}_b\\ v_b\end{array}\right]$$ 关于这个转换矩阵，我们有了新的定义 对于给定的$T=(R,p)\in SE(3)$，其伴随矩阵（adjoint representation）$[A{d}_T]$定义如下 $$[A{d}_T]=\left[\begin{array}{cc}R& 0\\ [p]R& R\end{array}\right]\in {\mathbb{R}}^{6\times 6}$$ 且 $${\mathcal{V}}^{\prime }=[A{d}_T]\mathcal{V}$$ 也可以写成
$${\mathcal{V}}^{\prime }=A{d}_T(\mathcal{V})$$
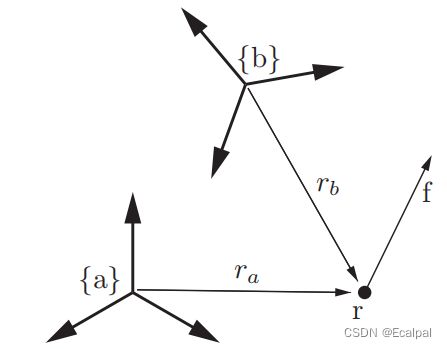
定义一个坐标系$a$，一个线性力作用于刚体上的某点$r$，$r_a\in {\mathbb{R}}^3$，则力$f_a\in {\mathbb{R}}^3$，则扭矩或者力矩可以写作$m_a=r_a\times f_a$，与速度旋量一样的表达方式，我们可以约定$${\mathcal{F}}_s=\left[\begin{array}{c}{m}_a\\ f_a\end{array}\right]\in {\mathbb{R}}^6$$
可以称作spatial force或者wrench，力旋量。
那么相对于$3\times 1$的速度/角速度和力/力矩表达方式，$6\times 1$的力旋量和速度旋量这种表达方式先进性体现在哪里？

首先，假设坐标系$a$到坐标系$b$的坐标变化$T$已知，如果要进行不同坐标系之间力的表达变化，我们可能要进行繁琐的推导，但是有一种更加高效简便的推导方法。
这边我们考虑到功率，通常与速度和力的乘积有关，并且功率是标量，在同一个系统中，不管是在哪个坐标系表示，系统的总能量总是保持不变的，那么可以用数学公式表示为
$${\mathcal{V}}_b^T{\mathcal{F}}_b={\mathcal{V}}_a^T{\mathcal{F}}_a$$
$${\mathcal{V}}_b^T{\mathcal{F}}_b=([A{d}_{T_{ab}}]{\mathcal{V}}_b{)}^T{\mathcal{F}}_a={\mathcal{V}}_b^T([A{d}_{T_{ab}}]{)}^T{\mathcal{F}}_a$$
化简得到 $${\mathcal{F}}_b=[A{d}_{T_{ab}}{]}^T{\mathcal{F}}_a=A{d}_{T_{ab}}^T({\mathcal{F}}_a)$$
$${\mathcal{F}}_a=[A{d}_{T_{ba}}{]}^T{\mathcal{F}}_b=A{d}_{T_{ba}}^T({\mathcal{F}}_b)$$
通常，使用固定坐标系 fixed space frame $s$和运动坐标系body frame $b$，
即spatial wrench ${\mathcal{F}}_s$和body wrench ${\mathcal{F}}_b$

在关节空间中，刚体动力学方程的形式如下
$$\tau -{\tau }_e=M(q)\ddot{q}+C(q,\dot{q})\dot{q}+g(q)$$
对于六轴机械臂，
$\dot{q},\ddot{q}\in {\mathbb{R}}^6$分别是关节空间下的角速度和角加速度；
$M(q)\in {\mathbb{R}}^{6\times 6}$是质量矩阵，对称正定惯性矩阵；
$C(q)\in {\mathbb{R}}^{6\times 6}$是离心力和哥氏力矩阵；
$g(q)\in {\mathbb{R}}^6$是重力矢量；
$\tau \in {\mathbb{R}}^6$是关节转矩矢量；
${\tau }_e\in {\mathbb{R}}^6$是作用在末端执行器上的外部力旋量对应的关节转矩矢量。
对应到笛卡尔空间下的刚体动力学方程
$$h_c-h_e=\Lambda (q){\dot{v}}_e+\Gamma (q,\dot{q})v_e+\eta (q)$$
作用在末端执行器上的虚拟力$\mathcal{F}$实际上可以用关节驱动器的驱动力表示，即$\tau =J^T(q)h$
关节空间和笛卡尔空间之间的可以进过如下变化得到
$$\tau -{\tau }_e=M(q)\ddot{q}+C(q,\dot{q})\dot{q}+g(q)$$
$$J^{-T}\tau -J^{-T}{\tau }_e=J^{-T}M(q)\ddot{q}+J^{-T}C(q,\dot{q})\dot{q}+J^{-T}g(q)$$
将$v_e=J\dot{q},{\dot{v}}_e=\dot{J}\dot{q}+J\ddot{q}$,即$\ddot{q}=J^{-1}{\dot{v}}_e-J^{-1}\dot{J}\dot{q}$,代入得到
$$J^{-T}\tau -J^{-T}{\tau }_e=J^{-T}M(q)J^{-1}{\dot{v}}_e-J^{-T}M(q)J^{-1}\dot{J}\dot{q}+J^{-T}C(q,\dot{q})J^{-1}{\dot{v}}_e+J^{-T}g(q)$$

那么，记
$\Lambda (q)=J^{-T}M(q)J^{-1}$表示笛卡尔空间下的惯性矩阵；
$\Gamma (q,\dot{q})=J^{-T}C(q,\dot{q})J^{-1}-\Lambda (q)J^{-1}\dot{J}$表示包含离心力和科氏力影响的旋量；
$\eta (q)=J^{-T}g(q)$表示重力影响的旋量；
以上是关节空间和笛卡尔空间之间刚体动力学的转化。
笛卡尔空间下的动力学方程表示为：
$$h_c-h_e=\Lambda (q)\dot{v}+\Gamma (q,\dot{q})\dot{v}+\eta (q)\text{\hspace{1em}(1)}$$

1 刚度控制(Stiffness Control)

末端执行器的位姿可以用$x_e=(p_e^T,{\varphi }_e^T{)}^T$，同样可以用$x_d$表示末端执行器期望位姿。

2 导纳控制

阻抗控制在机器人动力学的基础上，在加速度层面上对机器人动力学进行解耦和建模。当机器人与环境交互时，阻抗控制方程描述为：
$$h_c=\Lambda (q)\alpha +\Gamma (q,\dot{q})\dot{v}+h_e\text{\hspace{1em}(2)}$$
那么其实
$$\alpha =\dot{v}$$
$\alpha$的物理意义是相对于基座标系的末端执行器加速度旋量，是阻抗控制律的控制量。可以设置控制律：
$$\alpha ={\dot{v}}_d+M_d^{-1}[B_d(v_d-v_e)+h_{\Delta }-h_e]\text{\hspace{1em}(3)}$$
$$M_d({\dot{v}}_d-{\dot{v}}_e)+B_d(v_d-v_e)+h_{\Delta }=h_e\text{\hspace{1em}(4)}$$
其中，$M_d,B_d$分别表示惯性矩阵和阻尼矩阵，$h_e$表示与环境接触的弹性力旋量，$h_{\Delta }$由期望坐标系${\Sigma }_d$相对于末端执行器坐标${\Sigma }_e$的位姿变化产生的。在与刚性环境接触时，公式(4)转化为：
$$M_d({\dot{v}}_d-{\dot{v}}_e)+B_d(v_d-v_e)+K_d(x_d-x_e)=h_d-h_e\text{\hspace{1em}(5)}$$
其中，$D_d$表示刚度矩阵，$x_d,x_e$分别表示期望位姿和实际位姿。将位姿偏差量$(x_d-x_e)$和末端力误差量$(h_d-h_e)$作为导纳控制的输入，为了得到导纳控制的输出量$\alpha$，公式(5)可以转化为：
$$\alpha ={\dot{v}}_d+M_d^{-1}[\underset{\text{力空间相关量}}{(h_d-h_e)}+\underset{\text{位姿空间相关量}}{B_d(v_d-v_e)+K_d(x_d-x_e)}]\text{\hspace{1em}(6)}$$
在每个控制周期内对$\alpha$进行积分和二次积分分别可以得到期望速度$v_d$和期望位姿$x_d$，经过逆运动学控制机器人达到期望位姿，实现对机器人位姿的导纳控制，伪代码如表所示，其中导纳参数$K_d,B_d,M_d$需要根据经验和实验整定，其他输入参数均为实时获取或计算得到。

位姿导纳控制
输入：导纳参数$K_d,B_d,M_d$,期望速度旋量$v_d$,期望位姿$x_d$,实际位姿$x_d$,实际力旋量$h_e$
输出: 机器人末端位姿
1: 计算期望位姿与实际位姿的偏差量$err=x_d-x_e$
2: 计算式(6)中的位姿空间相关量$wrenc{h}_p=B_d(v_d-v_e)+K_d(x_d-x_e)$
3: 计算式(6)中的期望加速度${\alpha }_d=M_d^{-1}(h_d-h_e+wrenc{h}_p)$
4: 设置期望加速度阈值
5: 对期望加速度积分得到期望速度旋量$v_d$并纪录用于下一轮迭代
6: 对期望速度旋量$v_d$积分得到期望位姿$x_d$并纪录用于下一轮迭代
7: 设置期望位姿阈值
8: return $x_d$