【代码随想录训练营第42期 续Day52打卡 - 图论Part3 - 卡码网 103. 水流问题 104. 建造最大岛屿

目录

一、做题心得

二、题目与题解

题目一：卡码网 103. 水流问题

题目链接

题解：DFS

题目二：卡码网 104. 建造最大岛屿

题目链接

题解：DFS

 三、小结

---

一、做题心得

也是成功补上昨天的打卡了。

这里继续图论章节，还是选择使用 DFS 来解决这类搜索问题（单纯因为我更熟悉 DFS 一点），今天补卡的是水流问题和岛屿问题。个人感觉这一章节题对于刚入门图论还是挺有难度的，我们需要搞清楚 DFS 函数的作用，以及具体的代码书写，然后才是解题思路和优化的问题，毕竟这类题 DFS 函数部分的实现代码变化不大。

直接开始今天的内容。

二、题目与题解

题目一：卡码网 103. 水流问题

题目链接

103. 水流问题 (kamacoder.com)

题目描述

现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述

第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。 

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述

输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

输入示例

5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1

输出示例

0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1

提示信息

图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。 

数据范围：

1 <= M, N <= 100。

题解：DFS

题意：水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点，目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

思路：选择逆向思维：从第一组边界上的节点逆流而上，将遍历过的节点都标记上，同样从第二组边界的边上节点逆流而上，将遍历过的节点也标记上。然后两方都标记过的节点就是满足题意的坐标。

思路理清之后这题就不难了，分别从两组边界（4条边：上下左右边缘）开始进行 DFS 遍历并分别标记并记录两组逆向标记的结果，最终题目要求的节点就是两组标记结果的公共节点（都有标记）。

两组逆向标记的结果 -- 注意是 bool 类型对遍历的节点进行标记：

第一组边界：firstBorder

第二组边界：secondBorder

其他就跟之前打卡的岛屿问题差不多，这里不做过多解释，代码如下：

#include 
using namespace std;

int n, m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void dfs(vector> &grid, vector> &visited, int curx, int cury)
{
    if (visited[curx][cury]) // 如果当前节点已经被访问过，直接返回
        return;
    visited[curx][cury] = true; // 标记当前节点为已访问
    for (int i = 0; i < 4; i++)
    {
        int nextx = curx + dx[i];
        int nexty = cury + dy[i];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m)
            continue;
        if (grid[curx][cury] > grid[nextx][nexty]) // 注意：我们是逆向从低向高遍历 -- 那么从高到低（包括相等）情况直接跳过
            continue;
        dfs(grid, visited, nextx, nexty);
    }
    return;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m;
    vector> grid(n, vector(m, 0));
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> grid[i][j];
        }
    }
    // 标记从第一组边界上的节点出发，可以遍历的节点
    vector> firstBorder(n, vector(m, false));
    // 标记从第二组边界上的节点出发，可以遍历的节点
    vector> secondBorder(n, vector(m, false));
    // 从最上和最下行的节点出发，向高处遍历 -- 逆向
    for (int i = 0; i < n; i++)
    {
        dfs(grid, firstBorder, i, 0);      // 遍历最左列，接触第一组边界
        dfs(grid, secondBorder, i, m - 1); // 遍历最右列，接触第二组边界
    }
    // 从最左和最右列的节点出发，向高处遍历 -- 逆向
    for (int j = 0; j < m; j++)
    {
        dfs(grid, firstBorder, 0, j);      // 遍历最上行，接触第一组边界
        dfs(grid, secondBorder, n - 1, j); // 遍历最下行，接触第二组边界
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            if (firstBorder[i][j] && secondBorder[i][j]) // 如果这个节点，从第一组边界和第二组边界出发都遍历过（都有标记），就是结果
                cout << i << " " << j << endl;
        }
    }
}

题目二：卡码网 104. 建造最大岛屿

题目链接

104. 建造最大岛屿 (kamacoder.com)

题目描述

给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。

岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。

输入描述

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述

输出一个整数，表示最大的岛屿面积。

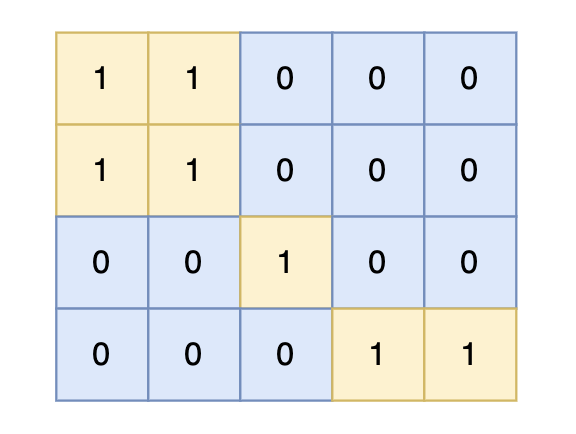
输入示例

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例

6

提示信息

对于上面的案例，有两个位置可将 0 变成 1，使得岛屿的面积最大，即 6。

数据范围：

1 <= M, N <= 50。

题解：DFS

之前打卡的岛屿问题的升级版。

本题的关键在于：如何有效地标记和计算每个岛屿的面积，以及如何找出添加一块陆地后能够连接的最大岛屿面积之和。

几个实现点：

深度优先搜索（DFS）：使用 dfs 函数来遍历地图，标记陆地，并计算岛屿面积。dfs 函数通过递归调用，遍历与当前节点相邻的陆地节点，并给每个陆地节点标记一个唯一的岛屿编号。

岛屿面积计算：在 dfs 函数中，通过一个计数器 cnt 来记录当前岛屿的面积。每当访问一个新的陆地节点时，cnt 加1。最后，将岛屿面积记录在哈希表 hash 中，键是岛屿编号，值是岛屿面积。

标记已访问的岛屿：使用一个布尔数组 visited 来标记每个节点是否已经被访问过。在 dfs 函数中，如果当前节点已经被访问过或者遇到海水，则直接返回，避免重复访问。

岛屿编号：岛屿编号从2开始，因为1已经被用作陆地，避免混淆。在 dfs 函数中，给每个陆地节点赋予一个新的岛屿编号。

计算添加陆地后的最大岛屿面积之和：遍历整个地图，对于每个位置，如果当前位置是陆地，则计算添加陆地后的岛屿面积之和。这通过遍历当前位置的四个相邻节点来实现，将相邻岛屿的面积加起来，并记录最大值。

代码如下：

#include 
using namespace std;

int n, m;
int cnt;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void dfs(vector> &grid, vector> &visited, int x, int y, int mark) // dfs函数用于标记岛屿，并计算岛屿面积
{
    if (visited[x][y] || grid[x][y] == 0) // 终止条件：访问过的节点 或者 遇到海水
        return;
    visited[x][y] = true; // 标记当前节点为已访问
    grid[x][y] = mark;    // 给陆地标记新标签
    cnt++;                // 岛屿面积 +1
    for (int i = 0; i < 4; i++)
    {
        int nextx = x + dx[i];
        int nexty = y + dy[i];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) // 越界 -- 跳过
            continue;
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int main()
{
    std::ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0); 
    cin >> n >> m;
    vector> grid(n, vector(m, 0));
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> grid[i][j];
        }
    }
    vector> visited(n, vector(m, false)); // 标记访问过的点
    unordered_map hash;                            // 哈希表：用于记录岛屿编号及其面积
    int mark = 2;                                            // 记录每个岛屿的编号，从2开始，因为1已经被用作陆地，避免异意
    bool isAllGrid = true;                                   // 标记是否整个地图都是陆地
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            if (grid[i][j] == 0) // 如果遇到海水，则整个地图不是全为陆地
                isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) // 如果节点未访问且为陆地
            {
                cnt = 0;                        // 重置岛屿面积计数
                dfs(grid, visited, i, j, mark); // 将与其链接的陆地（该岛屿）都标记上 true，并计算当前岛屿面积
                hash[mark] = cnt;               // 记录每一个岛屿的面积
                mark++;                         // 记录下一个岛屿编号
            }
        }
    }
    if (isAllGrid)
    {
        cout << n * m << endl; // 如果都是陆地，返回全面积
        return 0;              // 结束
    }
    // 计算添加一块陆地后，连接的岛屿面积之和的最大值
    int ans = 0;                    // 记录最后结果
    unordered_set visitedGrid; // 标记访问过的岛屿
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cnt = 1;             // 初始化岛屿数量，由于当前位置是陆地，所以初始值为1
            visitedGrid.clear(); // 清空已访问岛屿编号集合，准备计算新的岛屿面积之和
            if (grid[i][j] == 0)
            {
                for (int k = 0; k < 4; k++)
                {
                    int neari = i + dx[k]; // 计算相邻坐标
                    int nearj = j + dy[k];
                    if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) // 如果当前位置为海水，则计算添加陆地后的岛屿面积之和
                        continue;
                    if (visitedGrid.count(grid[neari][nearj])) // 如果相邻节点已经被访问过，则跳过 -- 即添加过的岛屿不要重复添加
                        continue; 
                    // 把相邻四面的岛屿数量加起来
                    cnt += hash[grid[neari][nearj]];        // 累加相邻岛屿的面积
                    visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
                }
            }
            ans = max(ans, cnt);
        }
    }
    cout << ans << endl;
}

 三、小结

水流问题和建造最大岛屿都是图论章节对于两大基本搜索的应用，我们需要掌握的不仅是 DFS 函数或者 BFS 函数的书写和作用，还有如何去优化处理将问题简单化。