dtw算法
dtw路径与线性变换路径对比
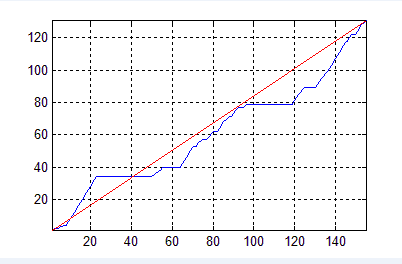
转自:http://baike.baidu.com/link?url=z4gFUEplOyqpgboea6My0mZPBh3_sZZpk6EfpzwuZ16uMlyPl7utZQi-XNkotLzLrGih9zUFNG4_tygNg8khiK
在孤立词
语音识别中,最为简单有效的方法是采用DTW(Dynamic Time Warping,动态时间归整)算法,该算法基于动态规划(DP)的思想,解决了发音长短不一的模板匹配问题,是语音识别中出现较早、较为经典的一种算法,用于孤立词识别。HMM算法在训练阶段需要提供大量的语音数据,通过反复计算才能得到模型参数,而DTW算法的训练中几乎不需要额外的计算。所以在孤立词
语音识别中,DTW算法仍然得到广泛的应用。
无论在训练和建立模板阶段还是在识别阶段,都先采用端点算法确定语音的起点和终点。已存入模板库的各个词条称为参考模板,一个参考模板可表示为R={R(1),R(2),……,R(m),……,R(M)},m为训练语音帧的时序标号,m=1为起点语音帧,m=M为终点语音帧,因此M为该模板所包含的语音帧总数,R(m)为第m帧的语音特征矢量。所要识别的一个输入词条语音称为测试模板,可表示为T={T(1),T(2),……,T(n),……,T(N)},n为测试语音帧的时序标号,n=1为起点语音帧,n=N为终点语音帧,因此N为该模板所包含的语音帧总数,T(n)为第n帧的语音特征矢量。参考模板与测试模板一般采用相同类型的特征矢量(如
MFCC,LPC系数)、相同的帧长、相同的窗函数和相同的帧移。
假设测试和参考模板分别用T和R表示,为了比较它们之间的相似度,可以计算它们之间的距离 D[T,R],距离越小则相似度越高。为了计算这一失真距离,应从T和R中各个对应帧之间的距离算起。设n和m分别是T和R中任意选择的帧号,d[T(n),R(m)]表示这两帧特征矢量之间的距离。距离函数取决于实际采用的距离度量,在DTW算法中通常采用欧氏距离。
若N=M则可以直接计算,否则要考虑将T(n)和R(m)对齐。对齐可以采用线性扩张的方法,如果N<M可以将T线性映射为一个M帧的序列,再计算它与{R(1),R(2),……,R(M)}之间的距离。但是这样的计算没有考虑到语音中各个段在不同情况下的持续时间会产生或长或短的变化,因此识别效果不可能最佳。因此更多的是采用动态规划(DP)的方法。
若把测试模板的各个帧号n=1~N在一个二维直角坐标系中的横轴上标出,把参考模板的各帧号m=1~M在纵轴上标出,通过这些表示帧号的整数坐标画出一些纵横线即可形成一个网络,网络中的每一个交叉点(n,m)表示测试模式中某一帧的交汇点。DP算法可以归结为寻找一条通过此网络中若干格点的路径,路径通过的格点即为测试和参考模板中进行计算的帧号。路径不是随意选择的,首先任何一种语音的发音快慢都有可能变化,但是其各部分的先后次序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束
为了描述这条路径,假设路径通过的所有格点依次为(n
1 ,m
1 ),……,(n
i ,m
j ),……,(n
N ,m
M ),其中(n
1,m
1 )=(1,1),(n
N ,m
M )=(N,M)。
路径可以用函数m = Oslash;(n )描述,其中n =i,i=1,2,……,N,Ø(1)=1,Ø(N)=M。为了使路径不至于过倾斜,可以约束斜率在0.5~2的范围内,如果路径已经通过了格点(n ,m ),
[1]
那么下一个通过的格点(n ,m )只可能是下列三种情况之一:
(n ,m )=(n +1,m +2)
(n ,m )=(n +1,m +1)
(n ,m )=(n +1,m )
用r表示上述三个约束条件。求最佳
路径的问题可以归结为满足约束条件r时,求最佳路径函数m =Ø(n ),使得沿路径的积累距离达到最小值,即:
搜索该路径的方法如下:搜索从(n ,m )点出发,可以展开若干条满足ŋ的路径,假设可计算每条路径达到(n ,m )点时的总的积累距离,具有最小累积距离者即为最佳路径。易于证明,限定范围的任一格点(n ,m )只可能有一条搜索路径通过。对于(ni,mi),其可达到该格点的前一个格点只可能是(n ,m )、(n ,m -1)和(n ,m -2),那么(n ,m )一定选择这3个距离之路径延伸而通过(n ,m ),这时此路径的积累距离为:
D[(n ,m )]=d[T(n ),R(m )]+D[(n , m )]
其中的n = n -1 ,m -1由下式决定:
D[(n ,m )]=min{D[(n , m )],D[(n , m -1)],D[(n , m -2)]}
这样可以从(n ,m )=(1,1)出发搜索(n ,m ),再搜索(n ,m ),……,对每一个(n ,m )都存储相应的前一格点(n ,m )及相应的帧匹配距离d[n ,m ]。搜索到(n ,m )时,只保留一条最佳路径。如果有必要的话,通过逐点向前寻找就可以求得整条路径。这套DP算法便是DTW算法。
DTW算法可以直接按上面描述来实现,即分配两个N×M的矩阵,分别为积累距离矩阵D和帧匹配距离矩阵d,其中帧匹配距离矩阵d(i,j)的值为测试模板的第i帧与参考模板的第j帧间的距离。D(N,M)即为最佳匹配路径所对应的匹配距离