Trie 树

看了很多 Trie 树的介绍， 这篇讲的最好,简单易懂(特别是代码部分)，直接转载：http://www.cnblogs.com/dolphin0520/archive/2011/10/11/2207886.html

Trie树也称字典树，因为其效率很高，所以在在字符串查找、前缀匹配等中应用很广泛，其高效率是以空间为代价的。

一.Trie树的原理

    利用串构建一个字典树，这个字典树保存了串的公共前缀信息，因此可以降低查询操作的复杂度。

    下面以英文单词构建的字典树为例，这棵Trie树中每个结点包括26个孩子结点，因为总共有26个英文字母(假设单词都是小写字母组成)。

    则可声明包含Trie树的结点信息的结构体:

1 #define MAX 26

2 

3 typedef struct TrieNode               //Trie结点声明 

4 {

5     bool isStr;                      //标记该结点处是否构成单词 

6     struct TrieNode *next[MAX];      //儿子分支 

7 }Trie;

　其中next是一个指针数组，存放着指向各个孩子结点的指针。

    如给出字符串"abc","ab","bd","dda"，根据该字符串序列构建一棵Trie树。则构建的树如下:

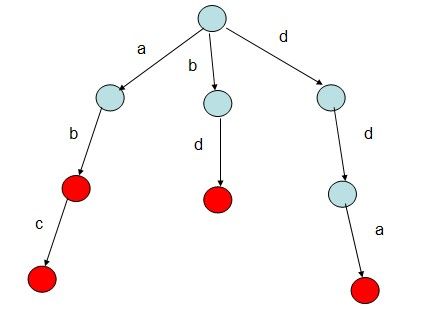
Trie树的根结点不包含任何信息，第一个字符串为"abc"，第一个字母为'a'，因此根结点中数组next下标为'a'-97的值不为NULL，其他同理，构建的Trie树如图所示，红色结点表示在该处可以构成一个单词。很显然，如果要查找单词"abc"是否存在，查找长度则为O(len)，len为要查找的字符串的长度。而若采用一般的逐个匹配查找，则查找长度为O(len*n)，n为字符串的个数。显然基于Trie树的查找效率要高很多。

但是却是以空间为代价的，比如图中每个结点所占的空间都为(26*4+1)Byte=105Byte，那么这棵Trie树所占的空间则为105*8Byte=840Byte，而普通的逐个查找所占空间只需(3+2+2+3)Byte=10Byte。

二.Trie树的操作

    在Trie树中主要有3个操作，插入、查找和删除。一般情况下Trie树中很少存在删除单独某个结点的情况，因此只考虑删除整棵树。

1.插入

  假设存在字符串str，Trie树的根结点为root。i=0，p=root。

  1)取str[i]，判断p->next[str[i]-97]是否为空，若为空，则建立结点temp，并将p->next[str[i]-97]指向temp，然后p指向temp；

   若不为空，则p=p->next[str[i]-97]；

  2)i++，继续取str[i]，循环1)中的操作，直到遇到结束符'\0'，此时将当前结点p中的isStr置为true。

2.查找

  假设要查找的字符串为str，Trie树的根结点为root，i=0，p=root

  1)取str[i]，判断判断p->next[str[i]-97]是否为空，若为空，则返回false；若不为空，则p=p->next[str[i]-97]，继续取字符。

  2)重复1)中的操作直到遇到结束符'\0',若当前结点p不为空并且isStr为true，则返回true，否则返回false。

3.删除

  删除可以以递归的形式进行删除。

测试程序:

 1 #include <iostream>

 2 #include <cstdlib>

 3 #include <stdio.h>

 4 #define MAX 26

 5 using namespace std;

 6 

 7 typedef struct TrieNode

 8 {

 9     bool isWord;

10     struct TrieNode *next[MAX];

11 }Trie;

12 

13 void insert(Trie *root, const char *s)

14 {

15     if(root == NULL || (*s) == '\0')

16         return;

17     Trie *p = root;

18     int i;

19     while((*s) != '\0')

20     {

21         if(p->next[(*s) - 'a'] == NULL)

22         {

23             Trie *temp = (Trie *)malloc(sizeof(Trie));

24             for(i = 0; i < MAX; ++i)

25             {

26                 temp->next[i] = NULL;

27             }

28             temp->isWord = false;

29             p->next[(*s) - 'a'] = temp;

30             p = p->next[(*s) - 'a'];

31         }

32         else

33         {

34             p = p->next[(*s) - 'a'];

35         }

36         s++;

37     }

38     p->isWord = true;

39 }

40 void del(Trie *root)

41 {

42     int i;

43     for(i = 0; i < MAX; ++i)

44     {

45         if(root->next[i] != NULL)

46         {

47             del(root->next[i]);

48         }

49     }

50     free(root);

51 }

52 

53 int search(Trie *root, const char *s)

54 {

55     Trie *p = root;

56     while(p != NULL&&*s != '\0')

57     {

58         p = p->next[(*s) - 'a'];

59         s++;

60     }

61     return (p != NULL && (p->isWord == true));

62 }

63 int main()

64 {

65     int i;

66     int n,m;

67     char s[100];

68     Trie *root = (Trie *)malloc(sizeof(Trie));

69     for(i = 0; i < MAX; ++i)

70     {

71         root->next[i] = NULL;

72     }

73     root->isWord = false;

74     scanf("%d",&n);

75     getchar();

76     for(i = 0; i < n; ++i)

77     {

78         scanf("%s",s);

79         insert(root, s);

80     }

81     while(scanf("%d",&m)!=EOF)

82     {

83         for(i = 0; i < m; ++i)

84         {

85             scanf("%s",s);

86             if(search(root, s))

87             {

88                 printf("Yes, find it!\n");

89             }

90             else

91             {

92                 printf("No, loss it!\n");

93             }

94         }

95     }

96     del(root);

97     return 0;

98 }