人工智能——状态空间搜索及状态空间表示法

1. 搜索

搜索（Search），设法在庞大状态空间图中找到目标。

主要分为两类性质的搜索：

• 基本搜索，是一种没有任何经验和知识起作用的、由某种规则所确定的非智能性的搜索；
• 启发式搜索（Heuristic Search）：其特点在于是一种有准备的、追求效率而有的放矢的智能搜索，它要求依据某种知识及信息的指导，通过逐一状态比较而找到符合规定条件的目标状态解。

 

2. 问题的状态空间图搜索

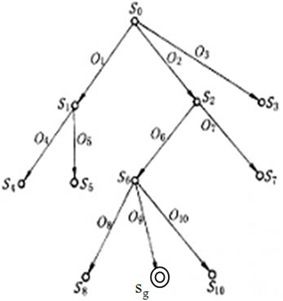
问题的状态空间可用有向图来表达，又常称其为状态树(State Tree)。图中，节点Sk表示状态，状态之间的连接采用有向弧(Arc)，弧上标以操作数OK来表示状态之间的转换关系。

图1 问题求解的状态树表示

用状态空间法搜索求解问题:

首先要把待求解的问题表示为状态空间图;

把问题的解表示为目标节点Sg。

求解就是要找到从根节点S0到达目标节点Sg的搜索路径。

状态空间图在计算机中有两种存储方式：一种是图的显式存储，另一种是图的隐式存储。

 

3. 状态空间表示法

状态空间

状态，描述某一类事物在不同时刻所处于的信息状况

操作，描述状态之间的关系

问题的状态空间可用一个三元序组来表示：

：问题的全部初始状态的集合

：操作的集合

：目标状态的集合

 

利用状态空间图求解的具体思路和步骤：

（1）设定状态变量及确定值域；

（2）确定状态组，分别列出初始状态集和目标状态集；

（3）定义并确定操作集；

（4）估计全部状态空间数，并尽可能列出全部状态空间或予以描述之；

（5）当状态数量不是很大时，按问题的有序元组画出状态空间图，依照状态空间图搜索求解。

 

传教士和野人问题（The Missionaries and Cannibals Problem）

在河的左岸有三个传教士、一条船和三个野人，传教士们想用这条船将所有的成员都运过河去，但是受到以下条件的限制：

① 教士和野人都会划船，但船一次最多只能装运两个；

② ②在任何岸边野人数目都不得超过传教士，否则传教士就会遭遇危险：被野人攻击甚至被吃掉。

此外，假定野人会服从任何一种过河安排，试规划出一个确保全部成员安全过河的计划。

 

（1）设定状态变量及确定值域。

为了建立这个问题的状态空间，设左岸传教士数为m，则

m ={0,1,2,3}；

对应右岸的传教士数为3－m； 左岸的野人数为c，则有

c ={0,1,2,3}；

对应右岸野人数为3－c；左岸船数为b，故又有b={0,1}，右岸的船数为1－b.

 

（2）确定状态组，分别列出初始状态集和目标状态集。

问题的状态可以用一个三元数组来描述，以左岸的状态来标记，即

Sk =（m,c,b），

右岸的状态可以不必标出。

初始状态一个： S0 =（3,3,1），初始状态表示全部成员在河的左岸；

目标状态也只一个： Sg =（0,0,0），表示全部成员从河左岸渡河完毕。

 

（3）定义并确定操作集。

仍然以河的左岸为基点来考虑，把船从左岸划向右岸定义为Pij操作。其中,第一下标i表示船载的传教士数, 第二下标j表示船载的野人数；同理，从右岸将船划回左岸称之为Qij操作，下标的定义同前。则共有10种操作，操作集为

F={P01，P10，P11，P02，P20，Q01，Q10，Q11，Q02，Q20}

 

（4）估计全部的状态空间数，并尽可能列出全部的状态空间或予以描述之。

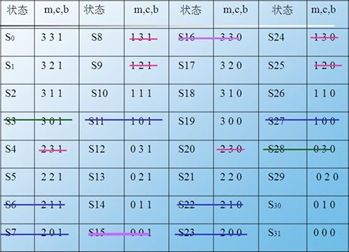
在这个问题世界中，S0 =（3,3,1）为初始状态，S31 = Sg =（0,0,0）为目标状态。全部的可能状态共有32个，如表所示。

表1 传教士和野人问题的全部可能状态

 

注意：按题目规定条件，应划去非法状态，从而加快搜索效率。

1）首先可以划去左岸边野人数目超过传教士的情况，即S4、S8、S9、S20、S24、S25等6种状态是不合法的；

2）应划去右岸边野人数目超过修道士的情况，即S6、S7、S11、S22、S23、S27等情况；

3）应划去4种不可能出现状态：划去S15和S16——船不可能停靠在无人的岸边；划去S3——传教士不可能在数量占优势的野人眼皮底下把船安全地划回来；划去S28——传教士也不可能在数量占优势的野人眼皮底下把船安全地划向对岸。可见，在状态空间中，真正符合题目规定条件的只有16个合理状态。

（5）当状态数量不是很大时，按问题的有序元组画出状态空间图，依照状态空间图搜索求解。

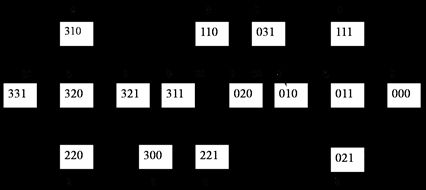
根据上述分析，共有16个合法状态和允许的操作，可以划出传教士和食人者问题的状态空间图，如图所示。

图2 传教士和野人问题的状态空间

任何一条从S0到达S31的路径都是该问题的解。

 

参考文献：

[1] 李长河. 人工智能及其应用. 北京: 机械工业大学出版社, 2006.8