Deep Learning 学习随记(八)CNN(Convolutional neural network)理解
前面Andrew Ng的讲义基本看完了。Andrew讲的真是通俗易懂,只是不过瘾啊,讲的太少了。趁着看完那章convolution and pooling, 自己又去翻了翻CNN的相关东西。
当时看讲义时,有一点是不太清楚的,就是讲义只讲了一次convolution和一次pooling,而且第一次的convolution很容易理解,针对一副图像来的,但是经过一次convolution和pooling
后,一副图像变成了好多副特征图(feature map)这时候再进行convolution时,该怎么办呢?所以去瞅了瞅CNN的相关论文。
CNN最经典的案例应该是LeNet-5这个数字识别的任务了吧。这里可以看下Yann Lecun大牛网页 http://yann.lecun.com/exdb/lenet/index.html, 以及tutorial: http://deeplearning.net/tutorial/lenet.html。
另外,一篇比较详细的讲CNN的中文博客(懒得看英语的话,就直接看这篇博客了):http://blog.csdn.net/zouxy09/article/details/8781543。
这里面都给出了CNN的结构图如下。
具体每个的含义这里也不说了,可以参考前面提到的资料。
看了结构图基本了解了。有几点一开始没看懂的需要说明的:
1. 关于每一个C层的feature map的个数。
比如C1是6个,C3是16个,这个应该是经验值,或者是通过实验给出的一个比较优的值,这点好多资料都没有说清楚。不过要注意的是,一般后面的要比前面的个数多些。
2. 关于后面的C层。比如S2到C3,并不是一一对应的。
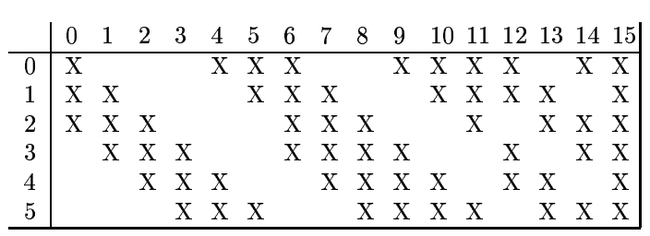
也就是说,并不是对S2中的每一个feature map与后面16个卷积核进行卷积。而是取其中几个。看了下面图应该很容易理解:
纵向是S2层的6个feature map,横向是C3的16个卷积核,X表示两者相连。比如说,第0个卷积核,只用在了前面3个feature map上,把这3个卷积结果加权相加或者平均就得到C3层的第一个(如按照上图标示应该是第0个)feature map。至于这个对应表示怎么来的,也不得而知啊,应该也是经验或者通过大量实验得来的吧。这点还不是很清楚...当然,如果想全部相连也不是不可以,只是对5个相加或者进行加权平均而已(比如第15号卷积核)。
3. 关于每一层的卷积核是怎么来的。
从Andrew的讲义中,我们是先从一些小patch里用稀疏自编码学习到100个特征(隐层100个单元),然后相当于100个卷积核(不知这样理解对不对)。这样子后面的卷积层的核怎么做呢?每一层都用前一层pooling(或者降采样)后得到的feature map再进行一次自编码学习?。这里就想到了去看toolbox里的CNN的代码,但感觉不是同一个套路:
下面是cnnsetup.m的代码:
function net = cnnsetup(net, x, y) inputmaps = 1; mapsize = size(squeeze(x(:, :, 1))); for l = 1 : numel(net.layers) % layer if strcmp(net.layers{l}.type, 's') mapsize = mapsize / net.layers{l}.scale; assert(all(floor(mapsize)==mapsize), ['Layer ' num2str(l) ' size must be integer. Actual: ' num2str(mapsize)]); for j = 1 : inputmaps net.layers{l}.b{j} = 0; end end if strcmp(net.layers{l}.type, 'c') mapsize = mapsize - net.layers{l}.kernelsize + 1; fan_out = net.layers{l}.outputmaps * net.layers{l}.kernelsize ^ 2; for j = 1 : net.layers{l}.outputmaps % output map fan_in = inputmaps * net.layers{l}.kernelsize ^ 2; for i = 1 : inputmaps % input map net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out)); end net.layers{l}.b{j} = 0; end inputmaps = net.layers{l}.outputmaps; end end % 'onum' is the number of labels, that's why it is calculated using size(y, 1). If you have 20 labels so the output of the network will be 20 neurons. % 'fvnum' is the number of output neurons at the last layer, the layer just before the output layer. % 'ffb' is the biases of the output neurons. % 'ffW' is the weights between the last layer and the output neurons. Note that the last layer is fully connected to the output layer, that's why the size of the weights is (onum * fvnum) fvnum = prod(mapsize) * inputmaps; onum = size(y, 1); net.ffb = zeros(onum, 1); net.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum)); end
里面inputmaps是上一层的feature map数。outputmaps当前层的feature map数。 其中有一行代码是
net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out));
这一句应该就是初始化卷积核了。这里是随机生成的一个在某个范围内的kernelsize*kernelsize的卷积核。其中i和j分别对应inputmaps和outputmaps。也就是说是为每一个连接初始化了一个卷积核。
下面再看下cnnff.m即前向传播的部分代码:
function net = cnnff(net, x) n = numel(net.layers); net.layers{1}.a{1} = x; inputmaps = 1; for l = 2 : n % for each layer if strcmp(net.layers{l}.type, 'c') % !!below can probably be handled by insane matrix operations for j = 1 : net.layers{l}.outputmaps % for each output map % create temp output map z = zeros(size(net.layers{l - 1}.a{1}) - [net.layers{l}.kernelsize - 1 net.layers{l}.kernelsize - 1 0]); for i = 1 : inputmaps % for each input map % convolve with corresponding kernel and add to temp output map z = z + convn(net.layers{l - 1}.a{i}, net.layers{l}.k{i}{j}, 'valid'); end % add bias, pass through nonlinearity net.layers{l}.a{j} = sigm(z + net.layers{l}.b{j}); end % set number of input maps to this layers number of outputmaps inputmaps = net.layers{l}.outputmaps; elseif strcmp(net.layers{l}.type, 's') % downsample for j = 1 : inputmaps z = convn(net.layers{l - 1}.a{j}, ones(net.layers{l}.scale) / (net.layers{l}.scale ^ 2), 'valid'); % !! replace with variable net.layers{l}.a{j} = z(1 : net.layers{l}.scale : end, 1 : net.layers{l}.scale : end, :); end end end % concatenate all end layer feature maps into vector net.fv = []; for j = 1 : numel(net.layers{n}.a) sa = size(net.layers{n}.a{j}); net.fv = [net.fv; reshape(net.layers{n}.a{j}, sa(1) * sa(2), sa(3))]; end % feedforward into output perceptrons net.o = sigm(net.ffW * net.fv + repmat(net.ffb, 1, size(net.fv, 2))); end
其中卷积层的代码确实是用了提前初始化的卷积核:
for j = 1 : net.layers{l}.outputmaps % for each output map % create temp output map z = zeros(size(net.layers{l - 1}.a{1}) - [net.layers{l}.kernelsize - 1 net.layers{l}.kernelsize - 1 0]); for i = 1 : inputmaps % for each input map % convolve with corresponding kernel and add to temp output map z = z + convn(net.layers{l - 1}.a{i}, net.layers{l}.k{i}{j}, 'valid'); end % add bias, pass through nonlinearity net.layers{l}.a{j} = sigm(z + net.layers{l}.b{j});
end
这里,使用的全连接的方式,不像2中提到的那样有选择性的连接。