微分起源
http://www.baike.com/wiki/%E5%BE%AE%E5%88%86
http://www.cnblogs.com/hustlzp/archive/2011/09/11/the-framework-of-the-calculus.html
以直代曲,以切线代曲线。
1. 微分由求给定曲线在给定点的切线问题开始的,求切线就是求导,就是得到Δy/Δx的极端值, 算出这个商的最终比。这个最开始研究的时候需要一点点计算出来,首先需要估计出Δy的值,Δy=f(x0+Δx)-f(x0)
要得到Δy/Δx的极端值,假设它有值,值等于A,那么Δy长什么样呢? Δy≈A×Δx,Δy=A×Δx+ο(Δx), ο(Δx)=Δy-A×Δxο(Δx),ο(Δx)大小怎么样呢?它应该是相对于Δy忽略不计的小,很小。伴随着Δx,Δy越来越小,ο(Δx)应该是越来越可以忽略掉了。
ο(Δx)是相比Δx的无穷小量,二者的比值ο(Δx)/Δx会无限接近0,而不是一个绝对值大于0的数,比如ο(Δx)是这样的(Δx)², (Δx)³, ln(Δx),
最精彩的地方是我们把ο(Δx)去掉,正如y=x²,在x=2处的切线,Δx=0.000000000000000001, Δy=4Δx+(Δx)²=0.000000000000000004000000000000000001≈0.000000000000000004, 因为0.000000000000000000000000000000000001相对于Δx或者Δy(Δy如果恒为0,在这里不适用)实在是太小了,对一座大山增删一两粒灰尘根本无损他的高度,灰尘相对于大山就是ο(Δx)相对于Δx。
2. 由求切线引起
若想可导,Δy得长什么样呢? Δy应该粗略可以表示成Δx的正比例,Δy≈A×Δx,Δy=A×Δx+ο(Δx),
或者说Δy得长什么样,怎么猜到是Δx线性表示,可能是由大量的计算得到的经验吧。
3. 也可能是已经有了切线了,由于数值计算的需要,要研究Δy的变化情况,再看看Δy的估计?
4. 微分是在x0点的最佳线性近似。注意,还有其他的线性近似,但是都不如微分近似程度高。哈哈哈。在近似计算的求微分的过程中,主要工作是把A×Δx独立出来,剩下的ο(Δx)放一起。独立出来的A×Δx部分,为了以后计算方便,把系数A整理到表里,下次再用的时候直接拿来就用,起个名字就叫微分主要系数吧。
4.1 但是如果不能做这种线性近似,也就是不可微,那就太打击人了。而事实上呢,绝大部分的连续函数都是不可微的,但是我们平常看到的函数绝大多数是可导的,万幸啊。
从导数到微分
和导数紧密关联的是微分的概念。从上面的论述中我们知道,为解决 “变化率” 问题,催化了导数概念的诞生。那么又是什么样的问题,导致了微分的诞生?
在很多具体问题中,我们 往往需要计算函数的改变量:
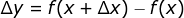
例如,求内半径为 r,厚度为 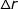 的球壳的体积,我们知道球体积公式为
的球壳的体积,我们知道球体积公式为 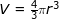 。当半径从 r 增加到 r +
。当半径从 r 增加到 r + 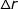 时,球的体积增加了
时,球的体积增加了
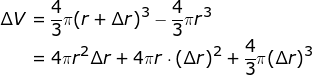
这里的函数 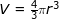 很简单,所以求
很简单,所以求  的表达式也不算太麻烦(三次式展开,再相减就行)。但是,有些函数非常复杂,此时求
的表达式也不算太麻烦(三次式展开,再相减就行)。但是,有些函数非常复杂,此时求 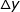 就不那么容易计算了。举个例子,现有函数
就不那么容易计算了。举个例子,现有函数 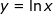 ,这时候你怎么求
,这时候你怎么求 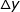 ?
?
嘿嘿,数学家们也考虑到这个问题了,有些东西硬算算不动,那就用 “近似” 呗!用一个相对简单的式子去近似那些无法直接计算的东西,不就 OK 了嘛!(虽然近似或多或少会造成误差,但是如果误差极小,趋近于 0,那就无所谓了)
此时,“微分” 的概念就快要 “粉墨登场” 了!
我们还是从导数的定义式出发:
![]()
若令:
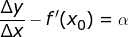
那么显然有  ,即当
,即当  时,
时,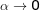 。对上式进行变形,有:
。对上式进行变形,有:
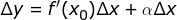
也就是说,给自变量 x 一个改变量 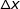 时,函数 y 获得的改变量
时,函数 y 获得的改变量 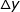 由两部分组成:一部分是
由两部分组成:一部分是 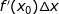 (线性部分);另一部分就是
(线性部分);另一部分就是 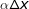 (非线性部分)。
(非线性部分)。
当  时,
时,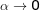 ,所以
,所以 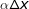 是一个比
是一个比 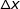 更快地趋向于零的一个量。也就是说,当
更快地趋向于零的一个量。也就是说,当 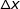 很小时,第一部分
很小时,第一部分 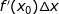 在
在 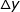 中所占的比例要比第二部分
中所占的比例要比第二部分 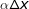 大得多。因此,可以把第二部分忽略不计。总的来说就是:当
大得多。因此,可以把第二部分忽略不计。总的来说就是:当 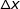 很小时,非线性部分会更快地趋向于 0,于是我们可以使用线性部分
很小时,非线性部分会更快地趋向于 0,于是我们可以使用线性部分 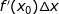 来近似
来近似 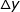 。
。
呵呵,我们可以为这个线性部分 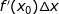 取一个名字 —— 微分,并用如下的符号表示:
取一个名字 —— 微分,并用如下的符号表示:
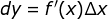
特别地,取 y = x,则有 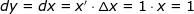 ,即
,即 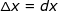 (此式表明:自变量的增量等于自变量的微分),因此上式可以改写为:
(此式表明:自变量的增量等于自变量的微分),因此上式可以改写为:
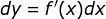
就这样,我们从导数的概念推出了微分的概念,微分描述了 当自变量 x 的改变 dx 足够小时,函数值 y 的改变 dy 可以用 f'(x)dx 来近似。你可能觉得,这有什么了不起的。不就是一个近似嘛。但是请仔细观察,当 x 是某个具体值的时候,f'(x) 可是一个常数!就是说 dy 和 dx 是成正比例的!进一步,就是说在 [x, x+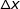 ] 区间内(
] 区间内(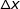 足够小),y = f(x) 可以近似看成一条直线段!而且
足够小),y = f(x) 可以近似看成一条直线段!而且 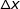 越小,这种近似越精确!这样一来,我们就可以用线性的方法来处理非线性的问题了,相当方便!
越小,这种近似越精确!这样一来,我们就可以用线性的方法来处理非线性的问题了,相当方便!
如果对上面的话还不太理解,看下面一张图,极其经典,说明了微分的几何意义:
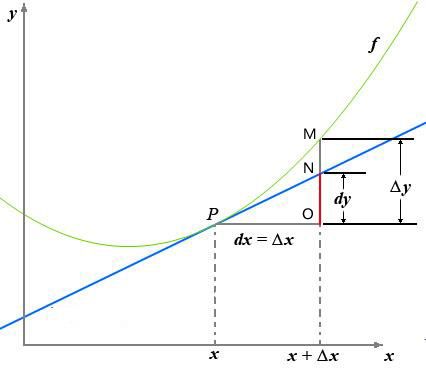
P 点和 M 点都在曲线上,其横坐标分别为 x 和 x+ 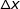 。
。
过 P 点做曲线切线交 OM 为 N,切线斜率即是导数 f'(x),那么 dy = f'(x) ▪ dx 则表示线段 ON。当  时,
时,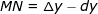 可以忽略不计,此时我们就可以用直线段 PN 来近似代替曲线段 PM 了。
可以忽略不计,此时我们就可以用直线段 PN 来近似代替曲线段 PM 了。
微分学综述
微分学,是研究函数局部特性的学科。导数和微分,是微分学中最重要的两个概念。
我们可以求出函数的导数 f'(x),它代表着函数在某点上因变量 y 相对于自变量 x 的变化率(从几何上来说,即是此点的切线的斜率);进一步,我们导出了微分的概念,它可以将复杂函数在局部范围内近似成线性函数,斜率即为此点的导数。这种线性近似,使得对复杂函数的研究在局部上得到简化,为后续的研究工作提供了强有力的支持。
增量无限趋近于零,割线无限趋近于切线,曲线无限趋近于直线,从而以直代曲,以线性化的方法解决非线性问题,这就是微分学理论的精髓所在。