Study notes for Expectation Maximum Algorithm

1. Introduction

• The EM algorithm is an efficient iterative procedure to compute the maximum likelihood (ML) estimate in the presence of missing or hidden data (variables). 
• It intends to estimate the model parameters such that the observed data are the most likely.

Convexity

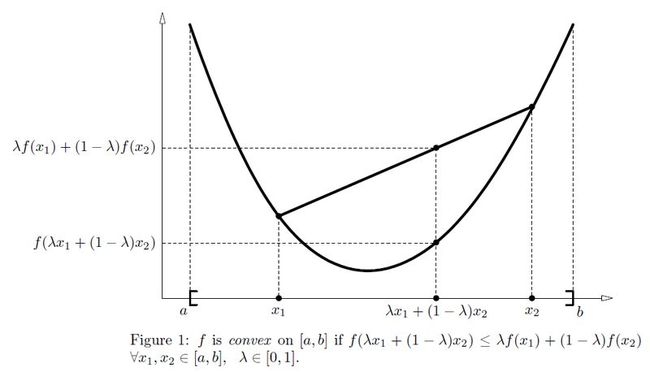
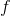• Let be a real function defined on an interval . 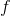is said to be convex on if,
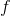  is said to be strictly convex if the inequality is strict. Intuitively, this definition states that the function falls below (strictly convex) or is never above (convex) the straight line from points  to .
  
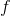• is concave (strictly concave) if  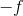is convex (strictly convex). 
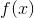• Theorem 1. If is twice differentiable on [a, b] and  on [a, b], then  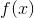is convex on [a, b].
  • If x takes vector values, f(x) is convex if the hessian matrix H is positive semi-definite (H>=0).
  • -ln(x) is strictly convex in (0, inf), and hence ln(x) is strictly concave in (0, inf).

Jensen's inequality

• The convexity is generalized to multivariate. 
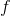• Let be a convex function defined on an interval. If and with,
  Note that holds true if and only if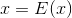 with probability 1, i.e., if X is a constant.
• Hence, for concave functions:
• Applying ln(x) and concavity, we can verify that,

2. The EM Algorithm

• Each iteration of the EM algorithm consists of two processes
  • E-step. The missing data are estimated, given the observed data and current estimate of the model parameters. The assumption is that the observed data is resulted from  the parameters of a model. 
  • M-step. The likelihood function is maximized under the assumption that the missing data are known. That is, the estimate of the missing data from the E-step are used in lieu of the actual missing data. The typical likelihood function is the log likelihood function defined as , i.e. a function of the parameter theta given the observed data X.
• Convergence is assured since the algorithm is guaranteed to increase the likelihood at each iteration.
• The detailed derivation can be referred to Andrew's or Sean's tutorial. 

Example

• Assume a model , where H is a hidden variable. We would like to estimate parameters: Pr(H), Pr(A|H), Pr(A|~H), Pr(B|H), Pr(B|~H). The observed data is given as follows:
  

  A	B	Count	Pr(H|A, B, params)
  0	0	6
  0	1	1
  1	0	1
  1	1	4

  • Initialize parameters: Pr(H)=0.4; Pr(A|H)=0.55; Pr(A|~H)=0.61; Pr(B|H)=0.43; Pr(B|~H)=0.52
  • E-step (estimate hidden variable):
    Pr(H|A, B) = Pr(A, B, H)/Pr(A, B) = Pr(A, B|H)Pr(H)/Pr(A, B) = Pr(A|H)Pr(B|H)Pr(H)/(Pr(A, B|H)Pr(H)+Pr(A, B|~H)(1-Pr(H)))
    =>Pr(H|~A, ~B, param)=0.48; Pr(H|~A, B, param)=0.39; Pr(H|A, ~B, param)=0.42;Pr(H|A, B, param)=0.33;
  • M-step (update parameters):
    =>Pr(H)=0.42; Pr(A|H)=0.35; Pr(A|~H)=0.46; Pr(B|H)=0.34; Pr(B|~H)=0.47;
  • Continue this procedure until the whole procedure keeps stable.

References

1. Andrew Ng, The EM algorithm: http://cs229.stanford.edu/materials.html.  
2. Sean Borman, The Expectation Maximization Algorithm: a short tutorial. 
3. Long Qin, Tutorial on Expectation-Maximization Algorithm.