划分树学习笔记

 

    今天没事就去刷以前hdu做过但是没过的题，前面的题现在还是能过的，做到这题就卡了，传说中的划分树，只闻其名未见其身。然后搜索了一下划分树的资料，擦擦擦，这不就是同快排的原理+线段树的操作，两者一融合进化成了划分树么。前面两个都会，学习起来倍感轻松。

 

 建树过程： 先对区间[1，n]内所有元素进行排序，未排序之前的数列赋值给线段树的第一层元素（tree[0][i]），然后就是同快排的原理以排序后中间元素为参照，小于它的放在树下一层的左边，大于它的放在树下一层的右边（划分树建树以中间元素为参照，快排以第一关键元素为参照）。然后再开一个sum数组，sum[d][i]表示第d层前i个元素有多少个元素小于as[mid]（as[mid]为排序后的中间值），这样一层一层建树下去最后建完树后等于对原数列排好了序。

 

查询过程： 这里最关键了。在查找区间[tl，tr]时，往下查询[tl，tr]左右孩子时，都要对区间[tl，tr]进行更新。

定义两个数s， ss，  d表示第d层， k（k表示要查询的第k元素） ：

s 表示区间[l，tl]有多少个元素小于as[mid]，  s=sum[d][tl-1]；

ss 表示区间[tl，tr]有多少个元素小于as[mid]， ss=sum[d][tr]-s；

if（ss>=k)  则下一层查询区间为[l+s，l+s+ss-1]；

else  则下一层查询区间为[mid+1+tl-l-s，mid+1+tr-l-s-ss];

自己懒，不愿画图多解释，借用一下小媛姐姐的图。

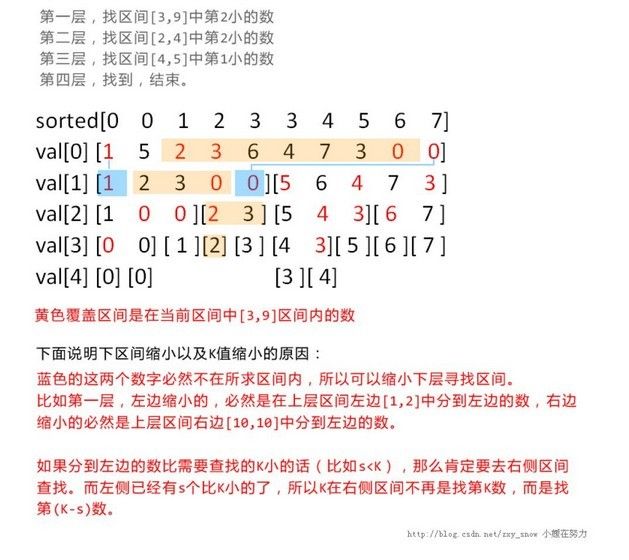
分析一下算法复杂度： 建树nlogn+查询mlogn，很强大的说。

题目链接：hdu2665 kth number

题目大意：O（-1）

解题思路：O（-1）

View Code

 1 #include <iostream>

 2 #include <cstdio>

 3 #include <cstring>

 4 #include <algorithm>

 5 using namespace std;

 6 

 7 const int maxn=100005;

 8 int sum[20][maxn], tree[20][maxn];

 9 int a[maxn], as[maxn]; ///原数组， 排序后数组

10 

11 void Build(int d, int l, int r)

12 {

13     int mid=(l+r)>>1, lp=l, rp=mid+1, lm=mid-l+1;

14     for(int i=l; i<=mid; i++)

15         if(as[i]<as[mid]) lm--; ///!!! 先假设前mid-l+1个数都等于as[mid]，as[i]比它小则减1

16     for(int i=l; i<=r; i++)

17     {

18         if(i==l) sum[d][i]=0;   ///sum[d][i]表示第d层前i个数有多少个小于as[mid]

19         else sum[d][i]=sum[d][i-1];

20         if(tree[d][i]==as[mid])

21         {

22             if(lm) lm--, sum[d][i]++, tree[d+1][lp++]=tree[d][i];

23             else tree[d+1][rp++]=tree[d][i];

24         }

25         else if(tree[d][i]<as[mid]) sum[d][i]++, tree[d+1][lp++]=tree[d][i];

26         else tree[d+1][rp++]=tree[d][i];

27     }

28     if(l==r) return ;

29     Build(d+1,l,mid);

30     Build(d+1,mid+1,r);

31 }

32 

33 int Query(int d, int l, int r, int tl, int tr, int k)

34 {

35     int s, ss, mid=(l+r)>>1;

36     if(l==r) return tree[d][l];

37     if(l==tl) s=0, ss=sum[d][tr]; ///！！特判

38     else s=sum[d][tl-1], ss=sum[d][tr]-s;

39     if(ss>=k) return Query(d+1,l,mid,l+s,l+s+ss-1,k);

40     else return Query(d+1,mid+1,r,mid+1+tl-l-s,mid+1+tr-l-s-ss,k-ss);

41 }

42 

43 int main()

44 {

45     int T, n, m;

46     cin >> T;

47     while(T--)

48     {

49         scanf("%d%d",&n,&m);

50         for(int i=1; i<=n; i++)

51         {

52             scanf("%d",a+i);

53             tree[0][i]=as[i]=a[i];

54         }

55         sort(as+1,as+n+1);

56         Build(0,1,n);

57         while(m--)

58         {

59             int l, r, k;

60             scanf("%d%d%d",&l,&r,&k);

61             int ans=Query(0,1,n,l,r,k);

62             printf("%d\n",ans);

63         }

64     }

65     return 0;

66 }

 

题目链接：hdu3743  minimum sum

题目大意：给你一个有n个数的数列，然后有m次询问[l，r]，让你在[l，r]中找一个数x使得|Xi-x|最小（l<=i<=r）.

解题思路：初中知识可知，形如|Xi-x|最小，那么必定是找排序后区间的中位数了。区间[l，r]的中位数必定是第k（（r-l+2）/2）位。

假设一段区间排序后是x1，x2，x3，x4，x5，x6，x7，x4是中位数，那么题要求的答案不就是（x4-x1）+（x4-x2）+（x4-x3）+（x5-x4）+（x6-x4）+（x7-x4）=（x5+x6+x7）-（x1+x2+x3）。   

结果分为了比中位数大的数和比中位数小的数，啊哈，这不就是要我们求第k元素么，这个k值固定了而已（中位数）。这里需要多开一个数组tol来记录第d层前i个数的和。当查询到第d层时，如果所求的ss比k大，则结果ans加上被分到右边的数，向左下层继续查询。如果ss比k小，则结果ans减去分到左边的数，向右下层继续查询。

注意区间奇偶判定以及数的范围。

View Code

 1 #include <iostream>

 2 #include <cstdio>

 3 #include <cstring>

 4 #include <algorithm>

 5 using namespace std;

 6 

 7 const int maxn=100005;

 8 typedef long long lld;

 9 int sum[20][maxn], tree[20][maxn];

10 lld tol[20][maxn];  ///!!!

11 int a[maxn], as[maxn];

12 

13 void Build(int d, int l, int r)

14 {

15     int mid=(l+r)>>1, lp=l, rp=mid+1, lm=mid-l+1;

16     for(int i=l; i<=r; i++)

17     {

18         if(as[i]<as[mid]) lm--;

19         if(i==l) tol[d][i]=tree[d][i];

20         else tol[d][i]=tol[d][i-1]+tree[d][i];

21     }

22     for(int i=l; i<=r; i++)

23     {

24         if(i==l) sum[d][i]=0;

25         else sum[d][i]=sum[d][i-1];

26         if(tree[d][i]==as[mid])

27         {

28             if(lm) lm--, sum[d][i]++, tree[d+1][lp++]=tree[d][i];

29             else tree[d+1][rp++]=tree[d][i];

30         }

31         else if(tree[d][i]<as[mid]) sum[d][i]++, tree[d+1][lp++]=tree[d][i];

32         else tree[d+1][rp++]=tree[d][i];

33     }

34     if(l==r) return ;

35     Build(d+1,l,mid);

36     Build(d+1,mid+1,r);

37 }

38 

39 lld Query(int d, int l, int r, int tl, int tr, int k, lld &ret)

40 {

41     if(l==r) return tree[d][l];

42     int mid=(l+r)>>1, s, ss, ql, qr;

43     if(tl==l) s=0, ss=sum[d][tr];

44     else s=sum[d][tl-1], ss=sum[d][tr]-s;

45     int x=tl-l-s, xx=tr-tl+1-ss;

46     if(ss>=k)

47     {

48         ql=mid+1+x, qr=ql+xx-1;

49         if(xx>0) ret+=tol[d+1][qr]-(x>0?tol[d+1][ql-1]:0);

50         return Query(d+1,l,mid,l+s,l+s+ss-1,k,ret);

51     }

52     else

53     {

54         ql=l+s, qr=l+s+ss-1;

55         if(ss>0) ret-=tol[d+1][qr]-(s>0?tol[d+1][ql-1]:0);

56         return Query(d+1,mid+1,r,mid+1+x,mid+1+x+xx-1,k-ss,ret);

57     }

58 }

59 

60 int main()

61 {

62     int n, m, T, tcase=0;

63     cin >> T;

64     while(T--)

65     {

66         scanf("%d",&n);

67         for(int i=1; i<=n; i++)

68         {

69             scanf("%d",a+i);

70             tree[0][i]=as[i]=a[i];

71         }

72         sort(as+1,as+n+1);

73         Build(0,1,n);

74         scanf("%d",&m);

75         printf("Case #%d:\n",++tcase);

76         while(m--)

77         {

78             int l, r;

79             scanf("%d%d",&l,&r);

80             lld ret=0, len=r-l+1;

81             lld tp=Query(0,1,n,l+1,r+1,(len+1)/2,ret);

82             if(len%2==0) ret-=tp;

83             printf("%I64d\n",ret);

84         }

85         puts("");

86     }

87     return 0;

88 }