hdu3483之二项式展开+矩阵快速幂

 

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 589    Accepted Submission(s): 305

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

 

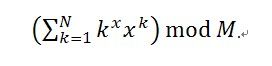
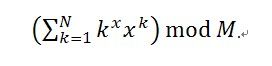
Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*10 ⁹, and 1 ≤ x ≤ 50.
The input ends up with three negative numbers, which should not be processed as a case.

 

 

Output

For each test case, print a line with an integer indicating the result.

 

 

Sample Input

100 1 10000 3 4 1000 -1 -1 -1

 

 

Sample Output

5050 444

/*分析:

Sn=1^x * x^1 + 2^x * x^2 +...+ n^x * x^n;

Sn+1=1^x * x^1 + 2^x * x^2 +...+ n^x * x^n+(n+1)^x * x^(n+1)=Sn+(n+1)^x * x^(n+1),将(n+1)^x二项式展开然后用矩阵快速幂

构造矩阵:

|1 xC(x,0) xC(x,1) xC(x,2) ... xC(x,x)|  |Sn	   | |S(n+1)		   |

|0 xC(0,0) 0       0       ... 0	  |  |x^n * n^0| |x^(n+1) * (n+1)^0|

|0 xC(1,0) xC(1,1) 0       ... 0	  | *|x^n * n^1|=|x^(n+1) * (n+1)^1|

|0 xC(2,0) xC(2,1) xC(2,2) ... 0	  |  |x^n * n^2| |x^(n+1) * (n+1)^2|

|...								  |  |...	   | |...			   |

|0 xC(x,0) xC(x,1) xC(x,2) ... xC(x,x)|  |x^n * n^x| |x^(n+1) * (n+1)^x|

*/

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<string>

#include<queue>

#include<algorithm>

#include<map>

#include<iomanip>

#define INF 99999999

using namespace std;



const int MAX=50+10;

__int64 array[MAX][MAX],sum[MAX][MAX],mod;



__int64 C(int n,int m){

	if(m<0 || m>n)return 0;

	__int64 ans=1;

	for(int i=1;i<=m;++i){

		ans=ans*(n-m+i)/i;

	}

	return ans%mod;

}



void MatrixInit(__int64 a[MAX][MAX],int &x,bool flag){

	a[0][0]=1;

	for(int j=1;j<=x+1;++j){

		if(flag)a[0][j]=x*C(x,j-1)%mod;

		else a[0][j]=0;

	} 

	for(int i=1;i<=x+1;++i){

		for(int j=0;j<=x+1;++j){

			if(flag)a[i][j]=x*C(i-1,j-1)%mod;

			else a[i][j]=(i == j);

		}

	}

}



void MatrixMult(__int64 a[MAX][MAX],__int64 b[MAX][MAX],int &x){

	__int64 c[MAX][MAX]={0};

	for(int i=0;i<=x+1;++i){

		for(int j=0;j<=x+1;++j){

			for(int k=0;k<=x+1;++k){

				c[i][j]=(c[i][j]+a[i][k]*b[k][j])%mod;

			}

		}

	}

	for(int i=0;i<=x+1;++i){

		for(int j=0;j<=x+1;++j)a[i][j]=c[i][j];

	}

}



__int64 MatrixPow(int &x,int &k){

	MatrixInit(sum,x,0);

	while(k){

		if(k&1)MatrixMult(sum,array,x);

		MatrixMult(array,array,x);

		k>>=1;

	}

	return sum[0][1];

}



int main(){

	int n,x;

	while(scanf("%d%d%I64d",&n,&x,&mod),n>0){

		MatrixInit(array,x,1);

		printf("%I64d\n",MatrixPow(x,n));

	}

	return 0;

}