常用字符串算法
简介
字符串的处理几乎无处不在,常用的字符串算法有KMP、扩展KMP、Trie树、AC自动机、Manacher、哈希、SA、SAM等。
Knuth-Morris-Pratt 算法
给你两个字符串AB,询问B串是否是A串的子串(A串是否包含B串)。
可以枚举从A串的什么位置起开始与B匹配,然后验证是否匹配。假如A串长度为n,B串长度为m,那么这种方法的复杂度是O (mn)的。
而KMP算法能够在线性复杂度内求出一个串在另一个串的所有匹配位置。
KMP的核心思想在于构建一个前缀数组(失配数组),对于模式串P,假设字符串下标从1开始,数组F满足F[i]=max{j|j<i且P[1..j]=P[i-j+1..i},即P的长度为j的前缀等于P的长度为i的前缀的长度为j的后缀。这说明F[i]所求的是串P[1..i]的一个最长的前缀P[1..j],这个前缀也是它的后缀。当这个前缀找不到的时候,F[i]设为0。
例如P=ababc,则F[4]=2,因为ab(P[1..2])是abab(P[1..4])的最长的前缀,又是它的后缀ab(P[3..4])。
有了F数组,就可以匹配两个字符串,主串T与模式串P。
先求出P的F数组,然后维护两个下标i和j,表示当前模式串P的前j个字符与主串T在位置i的前j个字符匹配,即P[1..j]=T[i-j+1..i]。
当算法在尝试对T[i+1]和P[j+1]匹配时,发现它们字符不同,那么就用F数组进行跳跃,使j=F[j]。
KMP算法高效的原因在于充分利用了匹配中的已有信息。关键的一步在于T[i+1]!=P[j+1]时j=F[j]。
因为我已知P[1..j]=T[i-j+1..i]而P[1..F[j]]=P[j-F[j]+1..j],因此P[1..F[j]]=T[i-F[j]+1..i],所以我们可以直接从F[j]位置开始继续匹配。
在实际实现中,字符串的下标从0开始,而我们仍然定义F数组的下标从1开始,对代码做一些简单的调整即可。

1 const int maxn=1111111; 2 char P[maxn]; 3 char T[maxn]; 4 int f[maxn]; 5 6 void getFail(char P[],int f[]){ 7 int i=0,j=-1; 8 int len=strlen(P); 9 f[0]=-1; 10 while (i<len){ 11 if (j==-1||P[i]==P[j]){ 12 i++,j++; 13 f[i]=j; 14 } 15 else{ 16 j=f[j]; 17 } 18 } 19 } 20 21 void KMP(char T[],char P[],int f[]){ 22 int i=0,j=0; 23 int n=strlen(T); 24 int m=strlen(P); 25 getFail(P,f); 26 while(i<n){ 27 if(j==-1||T[i]==P[j]){ 28 i++,j++; 29 } 30 else{ 31 j=f[j]; 32 } 33 if(j==m){ 34 // TO DO: 35 //ans++; 36 j=f[j]; 37 } 38 } 39 }
一些练习题
POJ 3461 Oulipo
计算单词W在整篇文章T中出现的次数。
KMP最基本的应用,统计出现次数,套模板即可。

1 if(j==m){ 2 // TO DO: 3 ans++; 4 j=f[j]; 5 }
POJ 2752 Seek the Name, Seek the Fame
找到一个S的子串作为前缀-后缀字符串。所谓前缀-后缀字符串即S的子串不仅是S的前缀又是S的后缀。
子串s[ 1 -> f[n] ] 是最长的子串,既是是s的前缀又是s的后缀,同理1 -> f[ f[n] ] 是次短的...依次递归。

1 while (f[n]>0){ 2 stk.push(f[n]); 3 n=f[n]; 4 }
POJ 2406 Power Strings
输出最大的n使得s由a重复n次而成。
当 n%(n-f[n])==0时,n-f[n] 是s最短的循环节。

1 if (n%(n-f[n])==0){ 2 printf("%d\n",n/(n-f[n])); 3 } 4 else{ 5 printf("1\n"); 6 }
POJ 1961 Period
对每个前缀i,若能由某些字符重复k次形成,输出最大的k。
与上题类似,枚举i,若i%(i-f[i])==0 则最短循环节为i-f[i],k为i/(i-f[i])

1 for (int i=2;i<=n;i++){ 2 if (f[i]>0&&i%(i-f[i])==0){ 3 printf("%d %d\n",i,i/(i-f[i])); 4 } 5 }
HDU 3336 Count the string
求出s有多少个子串是它本身的前缀。
DP公式如下。

1 for (int i=1;i<=n;i++){ 2 dp[i]=dp[f[i]]+1; 3 ans=(ans+dp[i])%10007; 4 }
HDU 3746 Cyclic Nacklace
至少要在字符串s后面补几个字符才能凑成一个循环。
若本身已经有循环节,则答案为0。

1 if (f[n]>0&&n%(n-f[n])==0) printf("0\n"); 2 else printf("%d\n",n-f[n]-n%(n-f[n]));
HDU 2087 剪花布条
给定T和P,为T中能分出几块P。
只匹配一次的KMP。当匹配成功时将j置为0即可。

1 if(j==m){ 2 // TO DO: 3 ans++; 4 j=0; 5 }
HDU 2594 Simpsons’ Hidden Talents
求a的最长前缀是b的后缀。
将两串拼接成s,a在前b在后,则问题转化为求一个串的前缀是后缀。
注意s的前缀不一定是a的前缀也不一定是b的后缀,所以当f[n]>na或f[n]>nb时我们要忽略子串s[ 1->f[n] ]。

1 while (f[m]>n1||f[m]>n2){ 2 m=f[m]; 3 } 4 if (f[m]>0){ 5 for (int i=0;i<f[m];i++){ 6 printf("%c",s1[i]); 7 } 8 printf(" %d\n",f[m]); 9 } 10 else{ 11 printf("0\n"); 12 }
hdu 4763 Theme Section
求出满足EAEBE格式的最长子串E的长度。
由最长前缀后缀推广而来。
首先由大到小枚举前缀后缀,对于每个前缀后缀f[x],在字符串中间寻找f[i]=f[x],若找到则输出答案,否则继续枚举。

1 int x=n; 2 bool flag=false; 3 while (f[x]>(n/3)) x=f[x]; 4 while (f[x]>0){ 5 flag=false; 6 for (int i=f[x]*2;i<=n-f[x];i++){ 7 if (f[i]==f[x]){ 8 flag=true; 9 break; 10 } 11 } 12 if (flag) break; 13 } 14 if (!flag) printf("0\n"); 15 else printf("%d\n",f[x]);
扩展 KMP 算法
给定主串S和模板串T,扩展KMP问题要求解的就是extend[1..|S|],其中extend[i]表示S[i..|S|]与T的最长公共前缀,即S中的每个后缀与T的最长公共前缀的长度。
对比KMP算法,发现当extend[i]=|T|时,T恰好在S中出现。因此该算法是KMP算法的进一步扩展,称为扩展KMP算法。
引入一个辅助数组next[1..|T|],其中next[i]表示后缀T[i..|T|]与T的最长公共前缀。
假设已经求好了extend[1..k],设当前i+extend[i]-1中的最大值为p,即之前匹配过程中到达过的最远位置。
设a+extend[a]-1=p,那么S[a..p]=T[1..p-a+1],由此可以推知S[k+1..p]=T[k-a+2,p-a+1]。
接下来就考虑T[k-a+2..|T|]与T的公共前缀长度,令L=next[k-a+2]。
分情况讨论:
- k+L<p。此时令extend[k+1]=L即可。
- k+L>=p。此时p之后的部分字符并不确定是否能匹配,所以从p+1位置开始进行暴力匹配。
在计算完了extend[k+1]之后,更新a和p继续。
next数组的计算实际就是T和T本身做扩展KMP的过程。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 const int MM=100005; 6 int next[MM],extand[MM]; 7 char S[MM],T[MM]; 8 void GetNext(const char *T){ 9 int len=strlen(T),a=0; 10 next[0]=len; 11 while(a<len-1 && T[a]==T[a+1]) a++; 12 next[1]=a; 13 a=1; 14 for(int k=2;k<len;k++){ 15 int p=a+next[a]-1,L=next[k-a]; 16 if( (k-1)+L >= p){ 17 int j = (p-k+1)>0 ? (p-k+1) : 0; 18 while(k+j<len && T[k+j]==T[j]) j++; 19 next[k]=j; 20 a=k; 21 } 22 else 23 next[k]=L; 24 } 25 } 26 void GetExtand(const char *S,const char *T){ 27 GetNext(T); 28 int slen=strlen(S),tlen=strlen(T),a=0; 29 int MinLen = slen < tlen ? slen : tlen; 30 while(a<MinLen && S[a]==T[a]) a++; 31 extand[0]=a; 32 a=0; 33 for(int k=1;k<slen;k++){ 34 int p=a+extand[a]-1, L=next[k-a]; 35 if( (k-1)+L >= p){ 36 int j= (p-k+1) > 0 ? (p-k+1) : 0; 37 while(k+j<slen && j<tlen && S[k+j]==T[j]) j++; 38 extand[k]=j; 39 a=k; 40 } 41 else 42 extand[k]=L; 43 } 44 } 45 int main(){ 46 while(scanf("%s%s",S,T)==2){ 47 GetExtand(S,T); 48 for(int i=0;i<strlen(T);i++) 49 printf("%d ",next[i]); 50 puts(""); 51 for(int i=0;i<strlen(S);i++) 52 printf("%d ",extand[i]); 53 puts(""); 54 } 55 return 0; 56 }
一些练习题
HDU 4333 Revolving Digits
读入数字串P,T由两个P拼接而成。
则T从0到n的每个长度为n的后缀即为一种数字排列。
对于T的后缀i,设其与原数字P的最长公共前缀长度为L。
若L>=n,说明此后缀表示的数与原数字相等。
若L<n,则令 T[i+extand[i]] 与 P[extand[i]] 比较大小即可得出两数的大小。
对于类似123123形式的重复串,排列三次以后又回到了123123的形式,所以答案必须除以循环节。
用KMP的找到最小循环节个数n/(n-f[n])

1 scanf("%s",P); 2 strcpy(T,P); 3 strcat(T,P); 4 GetExtand(T,P); 5 int n=strlen(P); 6 int cnt1=0,cnt2=0,cnt3=0; 7 for (int i=0;i<n;i++){ 8 if (extand[i]>=n) cnt2++; 9 else if (T[i+extand[i]]<P[extand[i]]) cnt1++; 10 else cnt3++; 11 } 12 getFail(P,f); 13 int tol=1; 14 if (n%(n-f[n])==0) tol=n/(n-f[n]); 15 printf("Case %d: %d %d %d\n",++Cas,cnt1/tol,cnt2/tol,cnt3/tol);
HDU 4300 Clairewd’s message
给一个密文到明文的映射表
给一个串,前面为密文,后面为明文,密文一定是完整的,但明文不完整或没有
将这个串补全。
令原串为T,将原串全部翻译为P。
可以发现原串T的后缀i是P的前缀。
从(n+1)/2开始枚举T的后缀,对于每个后缀i,若i+extand[i]>=n则从T:0~i-1为密文,P:i~n-1为明文。

1 GetExtand(T,P); 2 int ret=len; 3 for (int i=(len+1)/2;i<len;i++){ 4 if (extand[i]+i>=len){ 5 ret=i; 6 break; 7 } 8 }
Trie 树
Trie树又叫字典树或前缀树,是一种树形结构。
Trie可以看做是一个确定有穷自动机,它能接受所有字典中出现的单词。
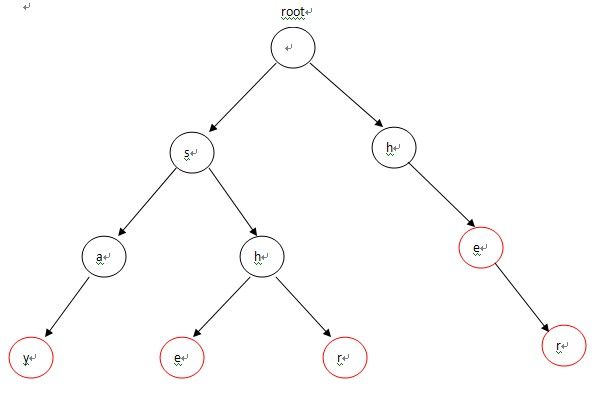
图中所示Trie可以接受4个单词,say,she,shr,her。
可以在Trie中插入,查找,删除一个字符串。
以插入为例:
- 从根结点开始,从前向后依次读入S的每个字符c。
- 如果当前结点没有一条指向孩子的边为c,那么新建这样一条边和一个孩子结点。
- 沿着c这条边走到下一层的结点。
- 如果还有下一个字符,回到第1步,否则标记当前结点为终结状态,结束。
Trie就好比维护了一个字典,可以在这个字典中插入删除查找字符串。复杂度都是O(m),m为插入串长度。
Trie的用途:
- Trie可以用来给字符串排序,把这些字符串插入Trie之后,先序遍历就是字典序。
- Trie的结点上可以储存额外的信息,每个结点上维护一个整数,每次经过该结点时将其加1即可。
- Trie上支持查找最长公共前缀的字符串。
- 可以实现自动补全功能。

1 const int CHARSET = 26; 2 const int MAX_N_NODES = int(3e5) + 10; 3 struct TrieNode 4 { 5 TrieNode* next[CHARSET]; 6 int num;//记录是不是一个单词 7 int value;//记录单词出现的次数 8 TrieNode(){ 9 memset(next,0,sizeof(next)); 10 value=0; 11 num=0; 12 } 13 void clear(){ 14 memset(next,0,sizeof(next)); 15 value=0; 16 num=0; 17 } 18 }*root; 19 TrieNode nodePool[MAX_N_NODES],*cur; 20 TrieNode* newNode(){ 21 TrieNode* t = cur++; 22 t->clear(); 23 return t; 24 } 25 void trieInit() { 26 cur=nodePool; 27 root=newNode(); 28 } 29 //插入: 30 void insert(char* s){ 31 TrieNode* p=root; 32 int k=0; 33 while(s[k]!='\0'){ 34 if(!p->next[s[k]-'a']) p->next[s[k]-'a']=newNode(); 35 p=p->next[s[k]-'a']; 36 p->num++; 37 k++; 38 } 39 p->value=1; 40 } 41 //查找 42 int find(char* s){ 43 TrieNode* p=root; 44 int k=0; 45 while(s[k]!='\0'&&p->next[s[k]-'a']){ 46 p=p->next[s[k]-'a']; 47 k++; 48 } 49 if(s[k]=='\0') return p->num; 50 return 0; 51 } 52 //DP查找 53 void dpfind(char* s,int pos){ 54 TrieNode* p=root; 55 int k=0; 56 while(s[k]!='\0'&&p->next[s[k]-'a']){ 57 p=p->next[s[k]-'a']; 58 if (p->value==1){ 59 //do something like dp... 60 //f[pos+k+1]=(f[pos+k+1]+f[pos])%MOD; 61 } 62 k++; 63 } 64 }
一些练习题
LA 3942 - Remember the Word
给出一个由S个不同单词组成的字典和一个长字符串,把这个字符串分解成若干个单词的链接,单词可以重复使用,有多少种方法?
f[i]表示以字符i为结尾的单词分解方法,若一个长度为x的单词与以i+1为开头的部分相匹配,则f[i+x]=f[i+x]+f[i];
将单词建立一个字典树,用字典树快速求出匹配的单词。

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <vector> 5 6 using namespace std; 7 8 char str[333333]; 9 char words[4444][111]; 10 int f[333333]; 11 12 //用类,或者结构体定义都行 13 struct trie 14 { 15 trie* next[26]; 16 int num; 17 int value; 18 trie() 19 { 20 for(int i=0;i<26;i++) next[i]=NULL; 21 value=0;//记录是不是一个单词 22 num=0;//记录单词出现的次数 23 } 24 void clear() 25 { 26 for(int i=0;i<26;i++) next[i]=NULL; 27 value=0;//记录是不是一个单词 28 num=0;//记录单词出现的次数 29 } 30 }root; 31 32 //插入: 33 void insert(char* s) 34 { 35 trie* p=&root; 36 int k=0; 37 while(s[k]!='\0') 38 { 39 if(!p->next[s[k]-'a']) p->next[s[k]-'a']=new trie; 40 p=p->next[s[k]-'a']; 41 p->num++; 42 k++; 43 } 44 p->value=1; 45 } 46 47 //查找 48 void find(char* s,int pos) 49 { 50 trie* p=&root; 51 int k=0; 52 while(s[k]!='\0'&&p->next[s[k]-'a']) 53 { 54 p=p->next[s[k]-'a']; 55 if (p->value==1) 56 { 57 f[pos+k+1]=(f[pos+k+1]+f[pos])%20071027; 58 } 59 k++; 60 } 61 } 62 63 int main() 64 { 65 int l,s; 66 int cnt=0; 67 while (~scanf("%s",str+1)) 68 { 69 cnt++; 70 memset(f,0,sizeof(f)); 71 root.clear(); 72 scanf("%d",&s); 73 l=strlen(str+1); 74 for (int i=0;i<s;i++) 75 { 76 scanf("%s",words[i]); 77 insert(words[i]); 78 } 79 f[0]=1; 80 for (int i=1;i<=l;i++) 81 { 82 if (f[i-1]) 83 { 84 find(str+i,i-1); 85 } 86 } 87 printf("Case %d: %d\n",cnt,f[l]); 88 } 89 return 0; 90 }
Aho-Corasick 自动机
AC自动机简介
AC自动机:Aho-Corasick automation,该算法在1975年产生于贝尔实验室,是著名的多模匹配算法之一。一个常见的例子就是给出n个单词,再给出一段包含m个字符的文章,让你找出有多少个单词在文章里出现过。
AC自动机的构造
- 构造一棵Trie,作为AC自动机的搜索数据结构。
- 构造fail指针,使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同 KMP算法一样, AC自动机在匹配时如果当前字符匹配失败,那么利用fail指针进行跳转。由此可知如果跳转,跳转后的串的前缀,必为跳转前的模式串的后缀并且跳转的新位置的深度(匹配字符个数)一定小于跳之前的节点。所以我们可以利用 bfs在 Trie上面进行 fail指针的求解。
- 扫描主串进行匹配。
一、Trie
首先我们需要建立一棵Trie。但是这棵Trie不是普通的Trie,而是带有一些特殊的性质。
首先会有3个重要的指针,分别为p, p->fail, temp。
1.指针p,指向当前匹配的字符。若p指向root,表示当前匹配的字符序列为空。(root是Trie入口,没有实际含义)。
2.指针p->fail,p的失败指针,指向与字符p相同的结点,若没有,则指向root。
3.指针temp,测试指针(自己命名的,容易理解!~),在建立fail指针时有寻找与p字符匹配的结点的作用,在扫描时作用最大,也最不好理解。
对于Trie树中的一个节点,对应一个序列s[1...m]。此时,p指向字符s[m]。若在下一个字符处失配,即p->next[s[m+1]] == NULL,则由失配指针跳到另一个节点(p->fail)处,该节点对应的序列为s[i...m]。若继续失配,则序列依次跳转直到序列为空或出现匹配。在此过程中,p的值一直在变化,但是p对应节点的字符没有发生变化。在此过程中,我们观察可知,最终求得得序列s则为最长公共后缀。另外,由于这个序列是从root开始到某一节点,则说明这个序列有可能是某些序列的前缀。
再次讨论p指针转移的意义。如果p指针在某一字符s[m+1]处失配(即p->next[s[m+1]] == NULL),则说明没有单词s[1...m+1]存在。此时,如果p的失配指针指向root,则说明当前序列的任意后缀不会是某个单词的前缀。如果p的失配指针不指向root,则说明序列s[i...m]是某一单词的前缀,于是跳转到p的失配指针,以s[i...m]为前缀继续匹配s[m+1]。
对于已经得到的序列s[1...m],由于s[i...m]可能是某单词的后缀,s[1...j]可能是某单词的前缀,所以s[1...m]中可能会出现单词。此时,p指向已匹配的字符,不能动。于是,令temp = p,然后依次测试s[1...m], s[i...m]是否是单词。
二、构造失败指针
用BFS来构造失败指针,与KMP算法相似的思想。
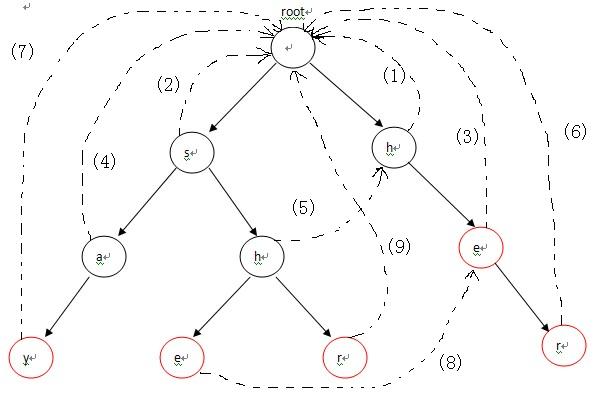
首先,root入队,第1次循环时处理与root相连的字符,也就是各个单词的第一个字符h和s,因为第一个字符不匹配需要重新匹配,所以第一个字符都指向root(root是Trie入口,没有实际含义)失败指针的指向对应下图中的(1),(2)两条虚线;第2次进入循环后,从队列中先弹出h,接下来p指向h节点的fail指针指向的节点,也就是root;p=p->fail也就是p=NULL说明匹配序列为空,则把节点e的fail指针指向root表示没有匹配序列,对应图-2中的(3),然后节点e进入队列;第3次循环时,弹出的第一个节点a的操作与上一步操作的节点e相同,把a的fail指针指向root,对应图-2中的(4),并入队;第4次进入循环时,弹出节点h(图中左边那个),这时操作略有不同。由于p->next[i]!=NULL(root有h这个儿子节点,图中右边那个),这样便把左边那个h节点的失败指针指向右边那个root的儿子节点h,对应图-2中的(5),然后h入队。以此类推:在循环结束后,所有的失败指针就是图-2中的这种形式。
三、扫描
构造好Trie和失败指针后,我们就可以对主串进行扫描了。这个过程和KMP算法很类似,但是也有一定的区别,主要是因为AC自动机处理的是多串模式,需要防止遗漏某个单词,所以引入temp指针。
匹配过程分两种情况:(1)当前字符匹配,表示从当前节点沿着树边有一条路径可以到达目标字符,此时只需沿该路径走向下一个节点继续匹配即可,目标字符串指针移向下个字符继续匹配;(2)当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,匹配过程随着指针指向root结束。重复这2个过程中的任意一个,直到模式串走到结尾为止。
对照上图,看一下模式匹配这个详细的流程,其中模式串为yasherhs。对于i=0,1。Trie中没有对应的路径,故不做任何操作;i=2,3,4时,指针p走到左下节点e。因为节点e的count信息为1,所以cnt+1,并且讲节点e的count值设置为-1,表示改单词已经出现过了,防止重复计数,最后temp指向e节点的失败指针所指向的节点继续查找,以此类推,最后temp指向root,退出while循环,这个过程中count增加了2。表示找到了2个单词she和he。当i=5时,程序进入第5行,p指向其失败指针的节点,也就是右边那个e节点,随后在第6行指向r节点,r节点的count值为1,从而count+1,循环直到temp指向root为止。最后i=6,7时,找不到任何匹配,匹配过程结束。
构造AC自动机中最重要的是构造失败指针。这里详细说一下失败指针的构建方法。
用fail[i]表示结点i对应的失败指针,fa[i]表示结点i在Trie树上的父结点,假设从fa[i]到i的那条边上的字符为c。
首先看fail[fa[i]]是否有条同样为c的边,如果是,则fail[i]即为fail[fa[i]]标着c的那条边指向的子结点,否则继续检查fail[fail[fa[i]]]。如果不停的向上到根仍然无法找到满足条件的结点,则表示Trie上没有串与结点i的路径字符串某个后缀相同,那么其fail指针指向根结点。

1 const int CHARSET = 26; 2 const int MAX_N_NODES = int(3e5) + 10; 3 4 struct Aho_Corasick{ 5 struct Node{ 6 Node *next[CHARSET]; 7 Node *fail; 8 int count;//记录当前前缀是完整单词出现的个数 9 Node(){ 10 memset(next,0,sizeof(next)); 11 fail = NULL; 12 count = 0; 13 } 14 void clear(){ 15 memset(next,0,sizeof(next)); 16 fail = NULL; 17 count = 0; 18 } 19 }; 20 Node *root; 21 Node nodePool[MAX_N_NODES], *cur; 22 Node* newNode(){ 23 Node* t=cur++; 24 t->clear(); 25 return t; 26 } 27 void init(){ 28 cur=nodePool; 29 root=newNode(); 30 } 31 void insert(char *str){ 32 Node* p=root; 33 int i=0,index; 34 while(str[i]){ 35 index=str[i]-'a'; 36 if(p->next[index]==NULL) p->next[index]=newNode(); 37 p=p->next[index]; 38 i++; 39 } 40 p->count++; 41 } 42 void build_ac_automation(){ 43 int i; 44 queue<Node*>Q; 45 root->fail=NULL; 46 Q.push(root); 47 while(!Q.empty()){ 48 Node* temp=Q.front(); 49 Q.pop(); 50 Node* p=NULL; 51 for(i=0;i<CHARSET;i++){ 52 if(temp->next[i]!=NULL){//寻找当前子树的失败指针 53 p = temp->fail; 54 while(p!=NULL){ 55 if(p->next[i]!=NULL){//找到失败指针 56 temp->next[i]->fail=p->next[i]; 57 break; 58 } 59 p=p->fail; 60 } 61 if(p==NULL) temp->next[i]->fail=root;//无法获取,当前子树的失败指针为根 62 Q.push(temp->next[i]); 63 } 64 } 65 } 66 } 67 int query(char *str){//询问str中包含n个关键字中多少种即匹配 68 int i=0,cnt=0,index; 69 Node* p = root; 70 while(str[i]){ 71 index=str[i]-'a'; 72 while(p->next[index]==NULL&&p!=root) p=p->fail;//失配 73 p=p->next[index]; 74 if(p==NULL) p = root;//失配指针为根 75 Node* temp = p; 76 while(temp!=root&&temp->count!=-1){//寻找到当前位置为止是否出现关键字 77 cnt+=temp->count; 78 temp->count=-1; 79 temp=temp->fail; 80 } 81 i++; 82 } 83 return cnt; 84 } 85 };
字符串哈希
用O(n)的复杂来预处理字符串,使得可以在O(1)复杂度内求出任意一个子串的哈希值。
对于第i个字符,让它对哈希值的贡献值表示成s[i]×Pi,其中P为一个素数,这里第i个指的是从右往左数。
H(i)=s[i]+s[i+1]x+...s[n-2]x^(n-2-i)+s[n-1]x^(n-1-i)
Hash(i,L)=s[i]+s[i+1]x+...s[i+L-2]x^(L-2)+s[i+L-1]x^(L-1)=H[i]-H[i+L]*x^L
如此可以利用二分快速的求出两个后缀的LCP。
对于LCP(i,j),二分答案L,判断Hash(i,L)与Hash(j,L)是否相等。

1 #include <iostream> 2 #include <cstring> 3 #include <algorithm> 4 #include <cstdio> 5 using namespace std; 6 7 typedef unsigned long long ULL; 8 9 const int SIZE = 100003; 10 const int SEED = 13331; 11 const int MAX_N = 50000 + 10; 12 char s[MAX_N]; 13 struct HASH{ 14 ULL H[MAX_N]; 15 ULL XL[MAX_N]; 16 int len; 17 HASH(){} 18 void build(char *s){ 19 len=strlen(s); 20 H[len]=0; 21 XL[0]=1; 22 for (int i=len-1;i>=0;i--){ 23 H[i]=H[i+1]*SEED+s[i]; 24 XL[len-i]=XL[len-i-1]*SEED; 25 } 26 } 27 ULL hash(int i,int L){ 28 return H[i]-H[i+L]*XL[L]; 29 } 30 }hs;
后缀数组
见后缀数组
后缀自动机
