最小二乘法
一.背景
5月9号到北大去听hulu的讲座《推荐系统和计算广告在视频行业应用》,想到能见到传说中的项亮大神,特地拿了本《推荐系统实践》求签名。讲座开始,主讲人先问了下哪些同学有机器学习的背景,我恬不知耻的毅然举手,真是惭愧。后来主讲人在讲座中提到了最小二乘法,说这个是机器学习最基础的算法。神马,最基础,我咋不知道呢! 看来以后还是要对自己有清晰认识。
回来赶紧上百度,搜了下什么是最小二乘法。
先看下百度百科的介绍:最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
通过这段描述可以看出来,最小二乘法也是一种优化方法,求得目标函数的最优值。并且也可以用于曲线拟合,来解决回归问题。难怪《统计学习方法》中提到,回归学习最常用的损失函数是平方损失函数,在此情况下,回归问题可以著名的最小二乘法来解决。看来最小二乘法果然是机器学习领域做有名和有效的算法之一。
二. 最小二乘法
我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢? 监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。 (2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。 (3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即采用平方损失函数。
样本回归模型:
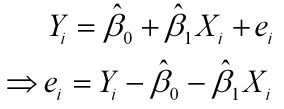 其中ei为样本(Xi, Yi)的误差
其中ei为样本(Xi, Yi)的误差
平方损失函数:

则通过Q最小确定这条直线,即确定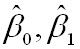 ,以
,以 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
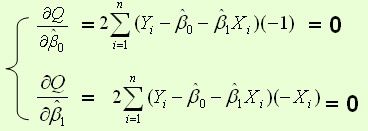
根据数学知识我们知道,函数的极值点为偏导为0的点。
解得:
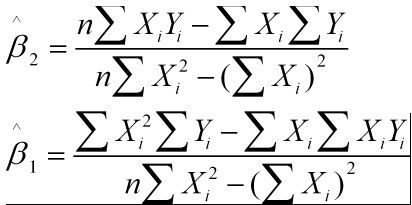
这就是最小二乘法的解法,就是求得平方损失函数的极值点。
三. C++实现代码
1 /* 2 最小二乘法C++实现 3 参数1为输入文件 4 输入 : x 5 输出: 预测的y 6 */ 7 #include<iostream> 8 #include<fstream> 9 #include<vector> 10 using namespace std; 11 12 class LeastSquare{ 13 double a, b; 14 public: 15 LeastSquare(const vector<double>& x, const vector<double>& y) 16 { 17 double t1=0, t2=0, t3=0, t4=0; 18 for(int i=0; i<x.size(); ++i) 19 { 20 t1 += x[i]*x[i]; 21 t2 += x[i]; 22 t3 += x[i]*y[i]; 23 t4 += y[i]; 24 } 25 a = (t3*x.size() - t2*t4) / (t1*x.size() - t2*t2); // 求得β1 26 b = (t1*t4 - t2*t3) / (t1*x.size() - t2*t2); // 求得β2 27 } 28 29 double getY(const double x) const 30 { 31 return a*x + b; 32 } 33 34 void print() const 35 { 36 cout<<"y = "<<a<<"x + "<<b<<"\n"; 37 } 38 39 }; 40 41 int main(int argc, char *argv[]) 42 { 43 if(argc != 2) 44 { 45 cout<<"Usage: DataFile.txt"<<endl; 46 return -1; 47 } 48 else 49 { 50 vector<double> x; 51 ifstream in(argv[1]); 52 for(double d; in>>d; ) 53 x.push_back(d); 54 int sz = x.size(); 55 vector<double> y(x.begin()+sz/2, x.end()); 56 x.resize(sz/2); 57 LeastSquare ls(x, y); 58 ls.print(); 59 60 cout<<"Input x:\n"; 61 double x0; 62 while(cin>>x0) 63 { 64 cout<<"y = "<<ls.getY(x0)<<endl; 65 cout<<"Input x:\n"; 66 } 67 } 68 }
四. 最小二乘法与梯度下降法
最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么区别呢。
相同
1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。 2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为:
![]()
其中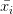 为第i组数据的independent variable,
为第i组数据的independent variable,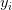 为第i组数据的dependent variable,
为第i组数据的dependent variable,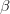 为系数向量。
为系数向量。
不同 1.实现方法和结果不同:最小二乘法是直接对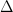 求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个
求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个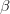 ,然后向
,然后向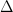 下降最快的方向调整
下降最快的方向调整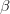 ,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html
