POJ3020-Antenna Placement
转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1299322779
提示:别被图片的圈圈误导了,看清楚题目,'*'是城市,'o'是空地,椭圆的天线覆盖范围要覆盖的是城市'*',而不是覆盖空地
题目大意:
一个矩形中,有N个城市’*’,现在这n个城市都要覆盖无线,若放置一个基站,那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线?
解题思路:
思前想后,依稀可以认为是一道求二分图的最小路径覆盖问题
(注意不是最小点覆盖)
那么接下来需要确认的是,
究竟是求 有向二分图的最小路覆盖,还是求 无向二分图的最小路覆盖
因为有向和无向是截然不同的计算方法。
要确认是构造有向图,还是构造无向图,那么就需要先根据题意,看看构造二分图时所使用的方式,更适合构造哪一种二分图。
然后就进入了本题难点:如何构造二分图
首先要明确的是,输入的一堆“圈圈星星”可以看做是一张大地图,地图上有所有城市的坐标,但是这里有一个误区:不能简单地把城市的两个x、y坐标作为准备构造的二分图的两个顶点集。
城市才是要构造的二分图的顶点!
构造方法如下:
例如输入:
*oo
***
O*o
时,可以抽象为一个数字地图:
100
234
050
数字就是根据输入的城市次序作为该城市的编号,0代表该位置没有城市。
然后根据题目的“范围”规则,从第一个城市开始,以自身作为中心城市,向四个方向的城市进行连线(覆盖)
因此就能够得到边集:
e12 e21 e32 e43 e53
e23 e34
e35
可以看到,这些边都是有向边,但是每一条边都有与其对应的一条相反边。
即任意两个城市(顶点)之间的边是成对出现的
那么我们就可以确定下来,应该 构造无向二分图(其实无向=双向)
因为若要构造有向的二分图时,需要判断已出现的边,是很麻烦的工作
为了把有向图G构造为无向二分图,这里需要引入一个新名词“拆点”
其实就是把原有向图G的每一个顶点都”拆分(我认为复制更准确)”为2个点,分别属于所要构造的二分图的两个顶点集
例如在刚才的例子中抽出一条有向边e12举例说明:
复制顶点1和顶点2,使得1,2∈V1;
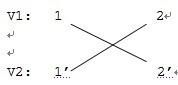
根据边e12和e21,得到无向二分图:
那么同理就可以得到刚才的例子的 无向二分图为:
再继而通过无向二分图,以V1的元素作为row,V2的元素作为col,构造 可达矩阵 存储到计算机
2 T F T F F
接下来就是要求这个 无向二分图的最小路径覆盖 了
利用公式:
无向二分图的最小路径覆盖 = 顶点数 – 最大二分匹配数/2
顶点数:就是用于构造无向二分图的城市数,即进行“拆点”操作前的顶点数量
最大二分匹配书之所以要除以2,是因为进行了“拆点”擦奥做做使得匹配总数多了一倍,因此除以2得到原图的真正的匹配数
最后剩下的问题就是求最大二分匹配数了,用匈牙利算法,这就不多说了,参考POJ3041的做法,基本一摸一样。
从这道题得出了一个结论:
当二分图的两个顶点子集基数相等时,该二分图所有顶点的匹配数 等于 任意一个顶点子集匹配数的2倍
其实匈牙利算法解题是极为简单的,但是图论的难并不是难在解答,而是建图的过程,也难怪会有牛曰:用匈牙利算法,建图是痛苦的,最后是快乐的。
1 //Memory Time
2 //420K 16MS
3
4 #include<iostream>
5 using namespace std;
6
7 int ipmap[41][11]; //标记存在城市'*'的位置,并依次记录城市的编号
8 int ip; //城市编号(最终是城市数量)
9 int V1,V2; //二分图的两个顶点集
10 int M; //最大二分匹配
11
12 bool city[401][401]; //标记两个城市之间是否能连通
13 //通过“拆点”操作,把每一个城市拆分为2个,分别属于所构造的二分图的两个点集
14 bool vist[401];
15 int link[401];
16
17 int dire_r[4]={-1,1,0,0};
18 int dire_c[4]={0,0,-1,1}; //分别对应四个方位 上 下 左 右
19
20
21 /*Hungary Algorithm*/
22
23 bool dfs(int x)
24 {
25 for(int y=1;y<=V2;y++)
26 if(city[x][y] && !vist[y])
27 {
28 vist[y]=true;
29 if(link[y]==0 || dfs(link[y]))
30 {
31 link[y]=x;
32 return true;
33 }
34 }
35 return false;
36 }
37
38 void search(void)
39 {
40 for(int x=1;x<=V1;x++)
41 {
42 memset(vist,false,sizeof(vist));
43 if(dfs(x))
44 M++;
45 }
46 return;
47 }
48
49 int main(void)
50 {
51 int test,h,w;
52 cin>>test;
53 while(test--)
54 {
55 /*Initial*/
56
57 memset(ipmap,0,sizeof(ipmap));
58 memset(city,false,sizeof(city));
59 memset(link,0,sizeof(link));
60 ip=0;
61 M=0;
62
63 /*Read in the maps*/
64
65 cin>>h>>w;
66
67 int i,j;
68 char temp;
69 for(i=1;i<=h;i++)
70 for(j=1;j<=w;j++)
71 {
72 cin>>temp;
73 if(temp=='*')
74 ipmap[i][j]=++ip;
75 }
76
77 /*Structure the Bipartite Graphs*/
78
79 for(i=1;i<=h;i++)
80 for(j=1;j<=w;j++)
81 if(ipmap[i][j])
82 for(int k=0;k<4;k++)
83 {
84 int x=i+dire_r[k];
85 int y=j+dire_c[k];
86 if(ipmap[x][y])
87 city[ ipmap[i][j] ][ ipmap[x][y] ]=true; //"拆点"操作是"顺便"被完成的
88 } //二分图构造完毕后,之后的问题就和POJ3041一样处理了
89
90 V1=V2=ip;
91
92 /*增广轨搜索*/
93
94 search();
95
96 /*Output*/
97
98 cout<<ip-M/2<<endl; //无向二分图:最小路径覆盖数 = "拆点"前原图的顶点数 - 最大匹配数/2
99 }
100 return 0;
101 }