数据结构之树和二叉树的一些基本概念

一、度和森林的定义

    ①、结点拥有的子树数称为结点的度

    ②、森林是M(M>=0)棵互不相交的树的集合

二、二叉树的一些性质

    ①、在二叉树的第i层上至多有2^(i-1)个结点(i>>1)

    ②、深度为k的二叉树至多有2^k - 1 个结点 :2^0 + 2^1 + 2^2 + ... + 2^(k-1) = 2^k - 1

    ③、对任何一颗二叉树T,如果其终端结点数为N0,度为2的结点数为N2,则N0 = N2 + 1

           证明:设T有N>0个结点,其度为1的结点有N1则有N = N0 + N1 + N2.一颗N个结点的二叉树需要N-1条线段来相连(暂且这么理解),则N - 1 = N1 + 2*N2 故N0 = N2 + 1

    ④、具有N个结点的完全二叉树的深度为[log(2)(N)]+1 ([X]表示不大于X的整数)

    ⑤、如果对一颗有N个结点的完全二叉树的结点按层序编号,则对任一结点i(1=<<i<<=n)有如下结论:

           (1)、如果2i > N,则结点i无左孩子,否则其左孩子为2i

           (2)、如果2i + 1> N,则结点i无右孩子,否则其右孩子为2i+1

   

三、二叉树的三种遍历:前序遍历、中序遍历、后序遍历.ABDGHCEIF、GDHBAEICF、GHDBIEFCA

四、线索二叉树的一些性质

    ①、线索二叉树中的所有叶子节点的左链域是线索指向其前驱.

          (1)、在中序线索二叉树中,如果叶子为其双亲节点的左孩子,则其前驱为其双亲节点的双亲节点.G是第一个访问的节点无前驱

          (2)、在中序线索二叉树中,如果叶子为其双亲节点的右孩子,则其前驱为其双亲节点.可对应上图中H的前驱为D和I的前驱是E. G是第一个访问的节点无前驱

    ②、线索二叉树中的所有叶子节点的右链域是线索指向其后继

          (1)、在中序线索二叉树中,如果叶子为其双亲节点的左孩子,则其后继为其双亲节点.可对应上图中G的后继为D.F是最后一个访问的节点无后继

          (2)、在中序线索二叉树中,如果叶子为其双亲节点的右孩子,则其后继为其双亲节点的************\/.可对应上图中H的后继是B和I的后继是C.F是最后一个访问的节点无后继

    ③、线索二叉树中的所有非终端节点的的右链域为指针时

          (1)、在中序线索二叉树中,该节点的后继是其右子树最左下的节点.可对应上图中D的后继为H和C的后继为F.F是最后一个访问的节点无后继

    ④、线索二叉树中的所有非终端节点的的左链域为线索时则指示其前驱.其左链域为线索时为指针时指向左子树

    ⑤、在后序线索二叉树中查找一个节点后继的情况:

          (1)、若节点是其双亲的右孩子或是其双亲的左孩子且其双亲木有右孩子,则其后继为双亲节点.可对应上图中F的后继为C、H的后继为D和I的后继为E

          (2)、若节点是双亲的左孩子且其双亲有右孩子,则其后继为其双亲右子树按后序遍历的第一个节点.可对应上图中B的后继为I和E的后继为F

五、树和二叉树之间的相互转换

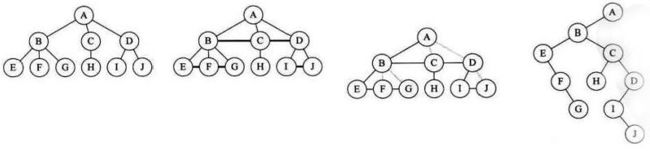
    ①、将树转化为二叉树

          (1)、加线.在所有兄弟结点之间加一条线

          (2)、去线.对树中的每个结点,只保留它与第一个孩子节点的连线,删除它与其它孩子结点之间的连线

          (3)、层次调整.第一个孩子是二叉树结点的左孩子,兄弟节点转换过来是结点的右孩子.