Trie树总结
现在有这样一道题:给你100000个长度不超过10的单词。对于每一个单词,我们要判断他出没出现过。
这个题很明显可以用HASH来做,但是对于长度不超过10的单词,trie树要来得更方便,效率也很好。不仅如此,trie树还有很多其他的用途,而且有些方面trie树有它独有的优势。比如说对于某一个单词,我要询问它的前缀是否出现过。这样hash就不好搞了,而用trie还是很简单。 现在回到例子中,如果我们用最傻的方法,对于每一个单词,我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd,那么在他前面的单词中,以b,c,d,f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的,在以a开头中的单词中,我们只要考虑以b作为第二个字母的……这就是trie树的基本模型了。
一、概述
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
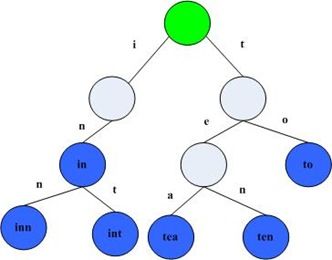
在该trie树中,字符串in,inn和int的公共前缀是“in”,因此可以只存储一份“in”以节省空间。当然,如果系统中存在大量字符串且这些字符串基本没有公共前缀,则相应的trie树将非常消耗内存,这也是trie树的一个缺点。
二、思维导图
三、题例分析
1、POJ2001:
题意:给出一系列单词,找出每个单词的的最短特征前缀。Trie树的入门题目
Code:
/***************************************************************
*Author: wanglikai91
*Date: 2011-10-10
***************************************************************/
#include <stdio.h>
#include <string.h>
const int MAXN = 1005, SIZE = 30;
char s[MAXN][SIZE];
struct node
{
int time; //记录含有此前缀的单词个数
node *next[SIZE];
node()
{
time = 0;
memset(next, NULL, sizeof(next));
}
}*root;
void insert(char *s) //插入操作
{
node *p = root;
int len = strlen(s), num;
for (int i = 0; i < len; ++i)
{
num = s[i] - 'a';
if (p->next[num] == NULL)
{
p->next[num] = new node;
p->next[num]->time = 1;
}
else
{
p->next[num]->time++;
}
p = p->next[num];
}
}
void find(char *s)
{
printf("%s ", s);
node *p = root;
int len = strlen(s), num;
for (int i = 0; i < len; ++i)
{
num = s[i] - 'a';
putchar(s[i]);
if (p->next[num]->time <= 1) //当出现次数小于等于1次时输出结束
{
putchar('\n');
return;
}
p = p->next[num];
}
putchar('\n'); //对于只有本身最为唯一前缀的单词整个单词输出才结束
}
int main()
{
int n = 0;
root = new node;
while (scanf("%s", s[n]) != EOF)
{
insert(s[n]);
++n;
}
for (int i = 0; i < n; ++i) find(s[i]);
return 0;
}
2、POJ3630:
题意:给出一系列电话号码,问是拨号是否会出错,出错即至少有一个号码是其他某个号码的前缀。
由于数据量较大,动态分配会超时,所以选择静态分配的写法。
Code:
/************************************************************************
*Author: wanglikai91
*Date: 2011-10-11
************************************************************************/
#include <stdio.h>
#include <string.h>
const int SIZE = 15, MAXN = 60000;
char s[SIZE];
struct node
{
bool flag;
node* next[10];
} po[MAXN];
int treesize;
bool insert(char *s)
{
bool ok = false; //用以标记此单词是否建立了新节点,如果没有肯定是前面出现过的某个单词的前缀
int len = strlen(s), num;
node *p = po;
for (int i = 0; i < len; ++i)
{
num = s[i] - '0';
if (p->next[num] == NULL)
{
ok = true;
p->next[num] = po + treesize++;
}
if (p->next[num]->flag) //如果之前加入的单词是当前插入单词的前缀返回false
{
return false;
}
p = p->next[num];
}
p->flag = true;
if (!ok) return false; //如果没有建立新节点返回false
return true;
}
int main()
{
int n, T;
scanf("%d", &T);
while (T--)
{
treesize = 1;
bool yes = true;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
{
scanf("%s", s);
if (yes && !insert(s))
{
yes = false;
}
}
if (yes)
{
puts("YES");
}
else puts("NO");
for (int i = 0; i < treesize; ++i) //初始化使用过的节点
{
po[i].flag = false;
memset(po[i].next, NULL, sizeof(po[i].next));
}
}
return 0;
}
四、模版
Code:
/*******************************************************************
*Author: wanglikai91
*Date: 2011-10-13
*******************************************************************/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
const int SIZE = 26;
class T_Node //节点类
{
public:
bool terminal; //是否是一个单词的结尾
T_Node *next[SIZE]; //节点儿子指针
public:
T_Node();
};
class Trie
{
public:
T_Node *root; //trie树的根
public:
Trie();
void Insert(string); //插入
bool Find(string); //查找
bool Delete(string); //删除
};
T_Node::T_Node() //节点构造函数,单词结尾设置为FALSE,初始化指针为空
{
terminal = false;
memset(next, NULL, sizeof(next));
}
Trie::Trie() //Trie树构造函数,建立根节点
{
root = new T_Node;
}
void Trie::Insert(string s) //插入
{
T_Node *p = root; //遍历指针*p初始化为根节点指针
int len = s.size(), num; //len单词长度
for (int i = 0; i < len; ++i)
{
num = s[i] - 'a'; //num当前单词对应表位置
if (p->next[num] == NULL)
{
p->next[num] = new T_Node; //当前字母指针不存在就建立新节点
}
p = p->next[num];
}
p->terminal = true;
}
bool Trie::Find(string s) //查找
{
T_Node *p = root;
int len = s.size(), num;
for (int i = 0; i < len; ++i)
{
num = s[i] - 'a';
if (p->next[num] == NULL) //某个字母不存在
{
return false;
}
p = p->next[num];
}
if (!p->terminal) return false; //单词没有在这里结尾
return true;
}
bool Trie::Delete(string s) //删除单词
{
T_Node *stack[105]; //用栈记录经过的节点
int top = 0;
T_Node *p = root;
int len = s.size(), num;
for (int i = 0; i < len; ++i)
{
num = s[i] - 'a';
if (p->next[num] == NULL) //没有这个单词
{
return false;
}
p = p->next[num];
stack[top++] = p;
}
if (!p->terminal) //没有这个单词
{
return false;
}
else
{
p->terminal = false; //去除标记
bool flag = true; //是否有冗余节点
while (flag && top > 0)
{
if (p->terminal)
{
flag = false;
}
else
{
for (int i = 0; i < SIZE; ++i)
{
if (p->next[i] != NULL)
{
flag = false;
break;
}
}
}
if (flag) //如果有冗余节点则删除
{
delete p;
}
p = stack[--top];
}
}
return true;
}
int main()
{
Trie tree;
string s;
s = "inn";
tree.Insert(s);
s = "int";
tree.Insert(s);
s = "tea";
tree.Insert(s);
s = "ten";
tree.Insert(s);
printf("Inserted 'inn', 'int', 'tea', 'ten'\n");
printf("Find:\n");
s = "ten";
if (tree.Find(s))
{
cout << s << " exist!" << endl;
}
else cout << s << " not exist!" << endl;
s = "itt";
if (tree.Find(s))
{
cout << s << " exist!" << endl;
}
else cout << s << " not exist!" << endl;
printf("Delete:\n");
s = "ten";
if (tree.Delete(s))
{
cout << s << " deleted!" << endl;
}
else cout << s << " not exist!" << endl;
s = "itt";
if (tree.Delete(s))
{
cout << s << " deleted!" << endl;
}
else cout << s << " not exist!" << endl;
printf("Check:\n");
s = "ten";
if (tree.Find(s))
{
cout << s << " exist!" << endl;
}
else cout << s << " not exist!" << endl;
return 0;
}