庖丁图解八皇后问题
八皇后问题是回溯算法中比较经典的案例。在 n × n 的棋盘中放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行、同一列、同一斜线上的棋子。
关于该题的解向量,我们可以用n元组x[1:n] 表示n后问题的解。其中,x[i] 表示皇后i放在棋盘的第i行的第x[i]列。例如说8皇后问题其中一个解可以表示如下,其中Q表示皇后所在的位置。

这里n 元组 x =[8,3,1,6,2,5,7,4],其对应的解是在棋盘的1,2,3….8行中,分别将皇后放在第8,3….4列上。
看到解向量后,我们很容易知道其解空间的结构是一个满n叉树。确定了解空间后,我们还需要将题目中给定的条件 “皇后不在同一行,同一列,同一斜线上” 转换为显示约束,从而在遍历解空间时可以裁剪掉无效的树节点。
我们取两个皇后所在位置的分别为 Q1 (i,x[i]) ,Q2 (j,x[j]), 那么不在同一行上的约束条件为i≠j,这点在定义解向量时已经进行了限定,可以不用考虑;不在同一列的约束条件为 x[i] ≠ x[j];而不在同一条斜线上的约束条件,如果把棋盘中心作为坐标原点,斜线上棋盘点构成的图形分别斜率为+1和-1的斜线,对应的图形函数分别是y=x+a,和y=-x+b,则约束条件可由下列公式推得
那么,根据上述约束条件和解向量的结构,我们可以写出一个剪枝函数来判断当前节点上得到的解是否满足约束条件,如果满足则继续搜索子树,否则剪去不可行的子树。
private boolean place(int k){
boolean placed = true;
for (int j = 1;j<k;j++){
if ((Math.abs(j-k) == Math.abs(_x[j] - _x[k])) || (_x[j] == _x[k])){
placed = false;
break;
}
}
return placed;
}
上面的剪枝函数的主要目的是每加入一个解向量的分量,则需要校验该分量是否与已有分量满足约束条件。例如遍历到当前节点所得到的解向量为[1, 3, 5, 7, 2, 4] 。这时,如果加入另一个分量5,则得到的解向量为[1,3,5,7,2,4,5],那这时调用上述剪枝函数时则会返回false,表示分量5不能与现有其他分量不满足约束条件,无法构成所需解。
有了剪枝函数后,下一步要做的是遍历解空间找到满足约束的解向量。第一种方法就是通过递归函数遍历解空间。
public void traceback(int i){
if (i > _n){
output_x();
}else{
for (int c = 1;c<=_n;c++){
_x[i] = c;
output_x();
if (place(i)) traceback(i + 1);
}
}
}
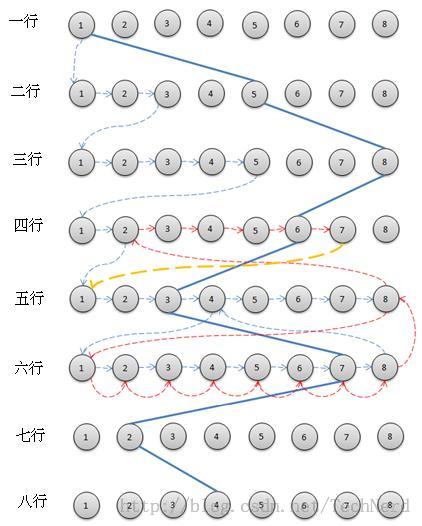
具体遍历过程如下图所示,由于篇幅的限制,我们不能也没必要画出解空间的完整的n叉树,所以,使用棋盘来说明遍历过程,自第二行以下每行的8个节点可以作为不同子树节点重复使用。首先从第一行的第一列(1,1)开始,沿着蓝色虚线到第二行的第一列(2,1),由于违反了约束条件,所以继续遍历第二行第二列(2,2),第三列(2,3),这时发现第二行第三列(2,3)与第一行的第一列(1,1)满足约束条件,于是从第二行的第三列(2,3)向子树递归,直到第五行的第四列(5,4), 由于第五行第四列与已有解向量分量[1,3,5,2]满足约束条件。所以,从此处继续向子树遍历,但发现第六行所有列与现有解向量分量[1,3,5,2,4]违反约束条件,搜索回溯到第五行第四列(5,4)并继续搜索至同一行的第八列(5,8),得到解向量[1,3,5,2,8]。这时候,从第五行第八列(5,8)遍历第六行子树(为了便于区分,红色虚线标示),第六行所有列都违反了约束条件即该行在当前解空间的递归路径[1,3,5,2,8] 下无解。这时,向上回溯至第四行的第二列(4,2),继续遍历至第四行第七列(4,7),得到解空间[1,3,5,7],继续向子树遍历(黄色虚线表示)。依照上述规则遍历n叉树,直到得到图中实线表示的一个解 [1, 5, 8, 6, 3, 7, 2, 4] 。
另一种遍历方式为非递归的迭代方式,这种方式较递归遍历稍微难理解一些,但其遍历的过程和思路与递归遍历基本是一样的,我们完全可以参考上面图解的遍历思路。
public void traceback(){
_x[1] = 0;
int k = 1;
while (k > 0){
_x[k] += 1;
while ((_x[k] <= _n) && !(place(k))) _x[k] += 1;
if (_x[k] <= _n)
if (k == _n) output_x();
else{
k++;
_x[k] = 0;
}
else k--;
}
}
由于递归的特点,递归遍历能够自动从子树一层一层循环上溯到根节点,但非递归的遍历方式就要自行决定当前遍历的层次,也就是对应代码中的k++ 和k-- 的操作。如果_x[k] > n ,就说明当前子树的遍历无法找到一个满足要求的皇后位置,这时候遍历层数就要向回退一层;否则,要向前加一层。
整体代码如下所示
package blog.csdn.net.technerd.queen;
public class NQueen {
private int _n; // 皇后个数
private int[] _x; //用来存储满足约束条件的解向量
public NQueen(int n){
this._n = n;
this._x = new int[_n + 1]; //创建一个n+1长度的数组,为了方便获取x[1...n]对应的解向量。
}
private void output_x() {
System.out.print(" ");
for (int i=1;i< _x.length;i++){
System.out.print(_x[i] + " ");
}
System.out.println();
graphic_output_x();
}
private void graphic_output_x() {
for (int i=1;i< _x.length;i++){
for (int j=1;j<=_n;j++){
if (j == 1) System.out.print(" ");
if (j == _x[i])
System.out.print( (char)81 + " ");
else
System.out.print((char)164 + " ");
}
System.out.println();
}
System.out.println("------------------------------");
}
/*
* 剪枝函数
*/
private boolean place(int k){
boolean placed = true;
for (int j = 1;j<k;j++){
if ((Math.abs(j-k) == Math.abs(_x[j] - _x[k])) || (_x[j] == _x[k])){
placed = false;
break;
}
}
return placed;
}
/**
* 递归遍历。调用例子 traceback(1);
*
*/
public void traceback(int i){
if (i > _n){ //当i大于n时,说明数组x中已经获得了一个满足约束条件的可用解。
output_x();
}else{
for (int c = 1;c<=_n;c++){
_x[i] = c;
output_x();
if (place(i)) traceback(i + 1);
}
}
}
/**
* 迭代遍历
*/
public void traceback(){
_x[1] = 0;
int k = 1;
while (k > 0){
_x[k] += 1;
while ((_x[k] <= _n) && !(place(k))) _x[k] += 1;
if (_x[k] <= _n) //当前子树有解
if (k == _n) output_x();
else{
k++;//找到当前层的一个可用解后,向下遍历其子树。
_x[k] = 0;
}
else k--; //当前子树无解,故向上回溯一层。
}
}
public static void main(String[] args){
NQueen n_queue = new NQueen(8);
//n_queue.traceback(1);
n_queue.traceback();
}
}
部分运行结果如下,篇幅所限,无法列出所有解。针对8皇后问题的可用解总数为92个。
1 5 8 6 3 7 2 4 Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ------------------------------ 1 6 8 3 7 4 2 5 Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ------------------------------ 1 7 4 6 8 2 5 3 Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ------------------------------ 1 7 5 8 2 4 6 3 Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ------------------------------ 2 4 6 8 3 1 7 5 ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ¤ ¤ Q ¤ ¤ ¤ ------------------------------