黄金连分数(高精度除法)

/*标题: 黄金连分数
黄金分割数0.61803... 是个无理数，这个常数十分重要，在许多工程问题中会出现。有时需要把这个数字求得很精确。
对于某些精密工程，常数的精度很重要。也许你听说过哈勃太空望远镜，它首次升空后就发现了一处人工加工错误，对那样一个庞然大物，其实只是镜面加工时有比头发丝还细许多倍的一处错误而已，却使它成了“近视眼”!!
言归正传，我们如何求得黄金分割数的尽可能精确的值呢？有许多方法。
比较简单的一种是用连分数：
 黄金数 = ---------------------
                        1
             1 + -----------------
                          1
                 1 + -------------
                            1
                     1 + ---------
                          1 + ...
这个连分数计算的“层数”越多，它的值越接近黄金分割数。
请你利用这一特性，求出黄金分割数的足够精确值，要求四舍五入到小数点后100位。
小数点后3位的值为：0.618
 小数点后4位的值为：0.6180
小数点后5位的值为：0.61803
小数点后7位的值为：0.6180340
（注意尾部的0，不能忽略）
你的任务是：写出精确到小数点后100位精度的黄金分割值。
注意：尾数的四舍五入！ 尾数是0也要保留！
显然答案是一个小数，其小数点后有100位数字，请通过浏览器直接提交该数字。
注意：不要提交解答过程，或其它辅助说明类的内容。
*/

#include"stdio.h"

#include"stdlib.h"

int a[101];//a保存小数结果

int c[9000];//用来保存被除数的每一位

int point;//记录小数点的位置



int print(int x[])

{int j;

 for(int i=999;i>=0;i--)

  if(x[i]!=0) { j=i; break; }

  for(int i=j;i>=0;i--)

   printf("%d",x[i]);

  printf("\n");

return 1;

} //输出一个数组中保存的值



int add(int x[],int y[])

{ int length_x,length_y;

int jinwei=0;//记录进位

int temp_y[1000];

for(int i=0;i<1000;i++)

{ if(x[i]==0) length_x=i;

  if(y[i]==0) length_y=i;

temp_y[i]=y[i];}//计算两个数字的长度

//x[0]保存最低位

for(int i=0;i<1000;i++)

{ y[i]=(x[i]+y[i])+jinwei;

 jinwei=y[i]/10;

 y[i]=y[i]%10;

//if(i<20)

 //printf("i=%d x_%d ,y_%d\n",i,x[i],y[i]);

}

for(int i=0;i<1000;i++)

x[i]=temp_y[i];

/*

printf("x:  ");

print(x);

printf("y:  ");

print(y);

*/

return 1;

}

int subcmp(int x[],int y[])

{//x[0]是最低位

int j_x,j_y,j,i;

 for(i=999;i>=0;i--)

  if(x[i]!=0) { j_x=i; break; }//确定最高位

  for(i=999;i>=0;i--)

  if(y[i]!=0) { j_y=i; break; }//确定最高位

  if(j_x>j_y) return 1;//x中的值大于y中的

  if(j_x<j_y) return -1;//x中的值小于于y中的

  if(j_x==j_y)//当两个数位数相同的时候

{for(i=j_x;i>=0;i--)

{if(x[i]>y[i]) return 1;

  if(x[i]<y[i]) return -1;}

return 0;

}

  

}//比较两个数数组里面保存的数字的大小



//两个数相减,结果保存在x[]中

int sub(int x[],int y[])

{//这里保证x[]>y[]

 int j_x,j_y,j,i;

 //for(i=999;i>=0;i--)

  //if(x[i]!=0) { j_x=i; break; }//确定最高位

  for(i=999;i>=0;i--)

  if(x[i]!=0) { j_y=i; break; }//确定最高位

//从数的地位到高位依次相减  

for(i=0;i<=j_y;i++)

{

 if(x[i]>=y[i]) {x[i]=x[i]-y[i]; continue;}

 if(x[i]<y[i])  {x[i]=x[i]+10-y[i]; x[i+1]--;  }

}

return 1;



}

int xiaoshu(int x[1000],int y[1000])

{  int xx[1000],yy[1000];

for(int i=0;i<1000;i++)

{yy[i]=y[i];

 xx[i]=x[i];}//将两个数组保存起来以防止干扰原数组的值



for(int i=0;i<101;i++)

{ if(subcmp(xx,yy)==-1)

   {a[i++]=0;

   for(int j=999;j>=1;j--)

   xx[j]=xx[j-1];

   xx[0]=0;//扩大十倍,相当于

}

while(subcmp(xx,yy)>=0)

{a[i]++;

sub(xx,yy);

}



 for(int j=999;j>=1;j--)

   xx[j]=xx[j-1];

   xx[0]=0;//每算完一位,扩大十倍



}//end for i



return 1;}



int main()

{int print(int x[]);

int add(int x[],int y[]);

int xiaoshu(int x[1000],int y[1000]);

long long int b[200];

int x[1000],y[1000];

int i;

b[0]=1;

b[1]=2;

for(i=0;i<101;i++)

{a[i]=0;

}

for(i=0;i<1000;i++)

{x[i]=y[i]=0;

}

x[0]=1;

y[0]=2;

for(i=0;i<300;i++)

add(x,y);

printf("此时被除数的值是:\n");

print(x);

printf("此时除数的值是:\n");

print(y);

xiaoshu(x,y);

//printf("%d",sub(y,x));



//xiaoshu(b[i-2],b[i-1]);



printf("0.");

for(i=1;i<101;i++)

{printf("%d ",a[i]);

if(i%10==0)

printf("\n");

}

printf("\n");

system("pause");}

 

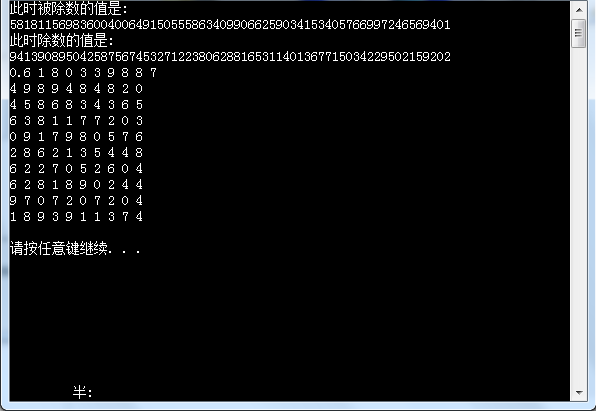
将上诉代码微微修改,可以求得更高精度的黄金分割数:

 

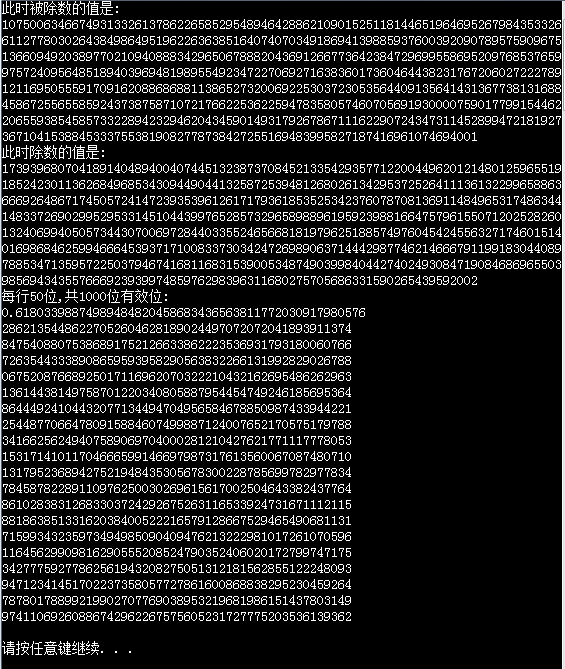
最后附上网络上给出的黄金分割点具体数字:

黄金分割数是无理数，前面的2000位为: 
  0.6180339887 4989484820 4586834365 6381177203 0917980576 : 50
  2862135448 6227052604 6281890244 9707207204 1893911374 : 100
  8475408807 5386891752 1266338622 2353693179 3180060766 : 150
  7263544333 8908659593 9582905638 3226613199 2829026788 : 200
  0675208766 8925017116 9620703222 1043216269 5486262963 : 250
  1361443814 9758701220 3408058879 5445474924 6185695364 : 300
  8644492410 4432077134 4947049565 8467885098 7433944221 : 350
  2544877066 4780915884 6074998871 2400765217 0575179788 : 400
  3416625624 9407589069 7040002812 1042762177 1117778053 : 450
  1531714101 1704666599 1466979873 1761356006 7087480710 : 500
  1317952368 9427521948 4353056783 0022878569 9782977834 : 550
  7845878228 9110976250 0302696156 1700250464 3382437764 : 600
  8610283831 2683303724 2926752631 1653392473 1671112115 : 650
  8818638513 3162038400 5222165791 2866752946 5490681131 : 700
  7159934323 5973494985 0904094762 1322298101 7261070596 : 750
  1164562990 9816290555 2085247903 5240602017 2799747175 : 800
  3427775927 7862561943 2082750513 1218156285 5122248093 : 850
  9471234145 1702237358 0577278616 0086883829 5230459264 : 900
  7878017889 9219902707 7690389532 1968198615 1437803149 : 950
  9741106926 0886742962 2675756052 3172777520 3536139362 : 1000
  1076738937 6455606060 5921658946 6759551900 4005559089 : 1050
  5022953094 2312482355 2122124154 4400647034 0565734797 : 1100
  6639723949 4994658457 8873039623 0903750339 9385621024 : 1150
  2369025138 6804145779 9569812244 5747178034 1731264532 : 1200
  2041639723 2134044449 4873023154 1767689375 2103068737 : 1250
  8803441700 9395440962 7955898678 7232095124 2689355730 : 1300
  9704509595 6844017555 1988192180 2064052905 5189349475 : 1350
  9260073485 2282101088 1946445442 2231889131 9294689622 : 1400
  0023014437 7026992300 7803085261 1807545192 8877050210 : 1450
  9684249362 7135925187 6077788466 5836150238 9134933331 : 1500
  2231053392 3213624319 2637289106 7050339928 2265263556 : 1550
  2090297986 4247275977 2565508615 4875435748 2647181414 : 1600
  5127000602 3890162077 7322449943 5308899909 5016803281 : 1650
  1219432048 1964387675 8633147985 7191139781 5397807476 : 1700
  1507722117 5082694586 3932045652 0989698555 6781410696 : 1750
  8372884058 7461033781 0544439094 3683583581 3811311689 : 1800
  9385557697 5484149144 5341509129 5407005019 4775486163 : 1850
  0754226417 2939468036 7319805861 8339183285 9913039607 : 1900
  2014455950 4497792120 7612478564 5916160837 0594987860 : 1950
  0697018940 9886400764 4361709334 1727091914 3365013715 : 2000