数据结构 练习 20-查找 算法
前言
分类
二分查找
原理就不多讲了 ,直接上代码吧!
void BinarySearch(int* Data,int n,int m,int key,int* loc)
{
if(n>=m) throw "invalid argument";
if(m-n==1)
{
if(Data[n]==key)
{
*loc=n;
}
if(Data[m]==key)
{
*loc=m;
}
return ;
}
int i=(m-n+1)/2;
if(key>Data[i])
{
BinarySearch( Data, i+1,m,key,loc);
}
if(key<Data[i])
{
BinarySearch(Data,n,i-1,key,loc);
}
if(key==Data[i])
*loc= i;
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[5]={1,3,6,8,9};
int key=8;
int i=-1;
int *loc=&i;
BinarySearch(a,0,4, key, loc);
std::cout<<*loc;
return 0;
}
复杂度lg(n)。
推荐一个JULY大牛写的:http://blog.csdn.net/v_july_v/article/details/7093204
Binary search的前提是 数组已经排好序。百度曾经有道面试题:在一个数组里查找绝对值最小的数,就是用这个思想。
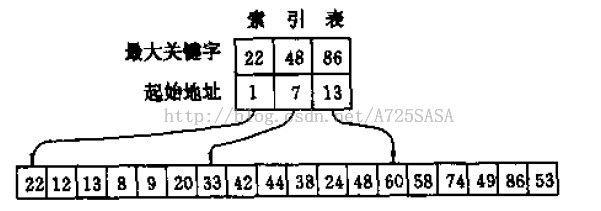
索引顺序表的查找
大体意思如下图,先对数组分块,然后抽取最大值。有点类似数据先清洗分解数据,按策略分开。复杂度看树高了。
二叉查找树
这是动态查找树的一种,操作包括:查找,删除,前驱,后继。与二分查找很相似,但是其插入,删除几乎不影响树的总体结构,即维护代价很小,因此常用作数据的查找。
查找,删除的平均复杂度跟lg(n)一个数量级。但是BST(binary search tree) 的形状不唯一,导致复杂度可能为O(n)(最坏)。为了防止这种情况,我们引入两种变型的二叉树。AVL(平衡二叉树),和RBT(红黑树)。
AVL
这种树的定义:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树(http://baike.baidu.com/view/593144.htm)。
AVL主要在二叉树的基础上维护BF(balance factor)<=1。如此一来,查找,删除的效率就不会出现不稳定,能维持在lg(n)。
为了在维护成本和查找,删除效率之间做个平衡,平衡二叉树出现了。它多了一个color,但是总体上树的层数不如AVL分布均匀,c++里的很多容器就是RBT。
RBT
红黑树的查找,删除的维护成本没有AVL高。这也是导致RBT查找效率不稳定的原因,凡是都是两面的。红黑树还引入了一个color,但是其维护成本也只有lg(n),不是很大。
因而,RBT在保持查找效率稳定的前提下,又没有增加太多的维护成本,不失为一种好的算法。其查找,删除复杂度能维持在lg(n)数量级。
B树,B+树
我们知道,红黑树在数据量小时,效率还是可以的。但是当数据量很大,数据没法装入内存时,问题就来了,如果我们把数据放到硬盘上,引入所谓的二次索引,那么对硬盘的I/O就很频繁了,导致速度很慢,因为硬盘的查询,等待,以及数据传输的时间跟内存的读取时间不在一个数量级上,因此对于像数据库索引,文件系统...我们要尽量提高查询,删除的速度。于是乎,B树应运而生,且不管哪个大牛发现的。B树试图只把根保留在内存,其余节点放在硬盘。那么为什么就减少了I/O呢?我们先来看看B树的定义吧:引用《算法导论》。
可见,B树的阶数不只是2时,这样可以大大降低高度,也就降低了访问磁盘的次数,而且B树的高度固定,为:log(ceil(m/2))((n+1)/2)。(记住)。
还有一种树B+,这种树的引入,进一步降低对I/O的访问。B+是在B的基础上改进,内部节点不存放关键字信息,全部关键字的信息放在叶子节点中。非终端节点存储关键字的索引信息。这样有俩个好处:
1 一个盘块能容纳的关键字数更多,减少了对I/O的访问;
2 每个节点的查找或是删除都是从根节点到叶子节点的查找,这样访问的效率很稳定。

