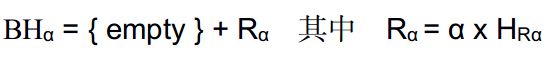纯函数式堆(纯函数式优先级队列)part three ---- bootstrapping (自举)
前言:
这篇文章是基于我看过的一篇论文,主要是关于函数式数据结构,函数式堆(优先级队列),
我会以自己的理解写下来,然后论文中出现的代码将会使用scala这们语言。
论文链接: Optimal Purely Functional Priority Queues,另外一个链接: 论文。
正文:
紧接patr two,
这章介绍对合并和查找操作的优化,使得最终插入,合并,查找最小的时间复杂度均为O(1)。
这里我跳过了论文中增加全局根那一节,因为bootstrap这一节包含了增加全局根的内容。
bootstrapping Heap:
首先假设原始堆的定义是:
a表示堆中存储的元素类型。
然后给出最终的bootstrap堆的定义:
这里BHa表示bootstrap堆或者是一个空堆或者是Ra(R代表root),
Ra表示一个元素a和一个原始堆H包含其他非空的bootstrap堆Ra的元组。
a其实就是保存堆中最小的元素,这样查找最小的操作时间复杂度就变为O(1)。
而这里原始堆H选用的当然就是斜二项堆,这样保持插入的时间复杂度O(1)。
而bootstrap堆的合并操作其实就变成将一个bootstrap堆作为元素插入到斜二项堆中。
这里对于斜二项堆中保存的元素类型就是Ra。
这里的定义有递归的感觉,读者最好是熟悉了前两章的内容再来看这章,
因为我是精简很多内容,所以如果觉得我说的不清楚的,可以看看论文解释的很详细。
我觉得看论文中的代码对于我的理解很有帮助。
现在来描述bootstrap堆的操作,这里用f来表示斜二项堆HRa的操作,F来表示bootstrap堆BHa的操作。
FINDEMIN( <x, sh> ) = x , <x, sh>就是Ra的表示, sh 表示HRa,就是斜二项堆;
INSERT( x, sh ) = MELD( <x, empty>, sh )
MELD( <x1, sh1>, <x2, sh2> ) = < x1, insert( <x2, sh2>, sh1 ) > if x1 <= x2
MELD( <x1, sh1>, <x2, sh2> ) = < x2, insert( <x1, sh1>, sh2 ) > if x2 < x1
DELETEMIN( <x, sh> ) = <y, meld( sh1, sh2 )>
其中 <y, sh1> = findMin( sh )
sh2 = deleteMin( sh )
我们可以看到
查找最小的操作FINDMIN明显时间复杂度为O(1),而对于合并操作MELD,时间复杂度的为O(1),因为斜二项堆的
插入操作是O(1),而插入操作其实就是化成合并操作MELD,所以时间复杂度为O(1),而对于删除最小操作,时间复杂
度是O(log n),因为对于斜二项堆findMin和deleteMin这两项的操作时间复杂度都是O(log n)。
bootsrtap堆的定义:
由于论文中的代码用的是ML语言,将之改成scala花了不少功夫:
trait BootstrapSkewBinomialHeap extends Heap {
//Rooted定义了斜二项堆的元素类型
trait Rooted extends Heap {
//RootQ就是上面定义的Ra,h表示堆的类型
//当该trait和斜二项堆trait混合的时候,就表示为斜二项堆的堆类型H
//就是下面的RootedHeap
case class RootQ( x: BootstrapSkewBinomialHeap.this.A, h: H)
override type A = RootQ
object AgeOrdering extends Ordering[RootQ] {
def compare( a: RootQ, b: RootQ ) =
BootstrapSkewBinomialHeap.this.ord.compare( a.x, b.x )
}
//因为堆的元素类型变为RootQ,所以需提供相应的元素比较方法
override def ord = AgeOrdering
}
//root斜二项堆
val RootedHeap = new Rooted with SkewBinomialHeap
//表示空bootstrap堆
case class Empty( msg: String )
//bootstrap堆的定义,或者是一个空堆,或者是一个RootQ类型
//用scala的Either类型来描述
override type H = Either[Empty, RootedHeap.RootQ]
override def empty = Left( Empty( "empty" ) )
override def isEmpty( ts: H ) = ts match {
case Left( _ ) => true
case Right( _ ) => false
}
//bootstrap堆的插入操作可化为合并操作
override def insert( x: A, ts: H ): H =
meld( Right( RootedHeap.RootQ( x, RootedHeap.empty ) ), ts )
override def meld( ts1: H, ts2: H ) = ( ts1, ts2 ) match {
case ( Left( Empty( _ ) ), ts ) => ts
case ( ts, Left( Empty( _ ) ) ) => ts
case ( Right( RootedHeap.RootQ( x1, h1: RootedHeap.H ) ),
Right( RootedHeap.RootQ( x2, h2: RootedHeap.H ) ) ) =>
//当两个bootstrap堆都非空的时候
//比较两个堆的根,较小的根作为新堆的根
//根较大的堆作为元素插入到根较小的斜二项堆中
if ( ord.lteq( x1, x2 ) )
Right(RootedHeap.RootQ(x1, RootedHeap.insert(ts2.right.get, h1)))
else
Right(RootedHeap.RootQ(x2, RootedHeap.insert(ts1.right.get, h2)))
}
override def findMin( ts: H ) = ts match {
case Left( Empty( _ ) ) =>
throw new NoSuchElementException("min of empty heap")
case Right( RootedHeap.RootQ( x, h ) ) => x
}
override def deleteMin( ts: H ) = ts match {
case Left( Empty( _ ) ) =>
throw new NoSuchElementException("delete min of empty heap")
case Right( RootedHeap.RootQ( x, h ) ) =>
if ( RootedHeap.isEmpty( h ) )
Left( Empty( "no element left" ) )
else {
//先查找斜二项堆h的最小元素(y, h1)
//然后删除斜二项堆h的最小元素
//最后返回新bootstrap堆,根为y,斜二项堆为h1和h2的合并
val RootedHeap.RootQ( y, h1 ) = RootedHeap.findMin( h )
val h2 = RootedHeap.deleteMin( h )
Right( RootedHeap.RootQ( y, RootedHeap.meld( h1, h2 ) ) )
}
}
}
另外一种定义方法:
我觉得这个表达更加清晰(新增2013-12-16):
trait BootstrapSkewBinomialHeap extends Heap {
trait Rooted extends Heap {
//这样定义是为了将空的bootstrap堆和非空bootstrap堆统一起来
trait RootType
case class RootQ( x: BootstrapSkewBinomialHeap.this.A, h: H) extends RootType
case object Empty extends RootType
override type A = RootQ
object AgeOrdering extends Ordering[RootQ] {
def compare( a: RootQ, b: RootQ ) =
BootstrapSkewBinomialHeap.this.ord.compare( a.x, b.x )
}
override def ord = AgeOrdering
}
val RootedHeap = new Rooted with SkewBinomialHeap
//这样就不用Either来表示了
override type H = RootedHeap.RootType
//这样表示空堆更加自然和可读
override def empty = RootedHeap.Empty
override def isEmpty( ts: H ) = ts match {
case RootedHeap.Empty => true
case RootedHeap.RootQ(_, _) => false
}
override def insert( x: A, ts: H ): H =
meld( RootedHeap.RootQ( x, RootedHeap.empty ), ts )
override def meld( ts1: H, ts2: H ) = ( ts1, ts2 ) match {
case ( RootedHeap.Empty, ts ) => ts
case ( ts, RootedHeap.Empty ) => ts
case ( RootedHeap.RootQ( x1, h1: RootedHeap.H ),
RootedHeap.RootQ( x2, h2: RootedHeap.H ) ) =>
if ( ord.lteq( x1, x2 ) )
RootedHeap.RootQ(x1,RootedHeap.insert(ts2.asInstanceOf[RootedHeap.RootQ],h1))
else
RootedHeap.RootQ(x2,RootedHeap.insert(ts1.asInstanceOf[RootedHeap.RootQ],h2))
}
override def findMin( ts: H ) = ts match {
case RootedHeap.Empty =>
throw new NoSuchElementException("min of empty heap")
case RootedHeap.RootQ( x, h ) => x
}
override def deleteMin( ts: H ) = ts match {
case RootedHeap.Empty =>
throw new NoSuchElementException("delete min of empty heap")
case RootedHeap.RootQ( x, h ) =>
if ( RootedHeap.isEmpty( h ) )
RootedHeap.Empty
else {
val RootedHeap.RootQ( y, h1 ) = RootedHeap.findMin( h )
val h2 = RootedHeap.deleteMin( h )
RootedHeap.RootQ( y, RootedHeap.meld( h1, h2 ) )
}
}
}
新的定义:
这几天又学到了scala新的技巧,觉得可以运用在bootstrap堆的定义上,
其实就是个小技巧,可以让代码更简洁(新增2013-12-21):
trait BootstrapSkewBinomialHeap extends Heap {
trait Rooted extends Heap {//。。。没有变化}
val RootedHeap = new Rooted with SkewBinomialHeap
//import 这一句就是技巧,对比上面发现
//之前表示继承RootType的RootQ和Empty前面都要加RootedHeap
//现在不用了,代码更简洁可读
import RootedHeap._
override type H = RootType
override def empty = Empty
override def isEmpty( ts: H ) = ts match {
case Empty => true
case RootQ(_, _) => false
}
override def insert( x: A, ts: H ): H = meld( RootQ( x, RootedHeap.empty ), ts )
override def meld( ts1: H, ts2: H ) = ( ts1, ts2 ) match {
case ( Empty, ts ) => ts
case ( ts, Empty ) => ts
case ( RootQ( x1, h1: RootedHeap.H ), RootQ( x2, h2: RootedHeap.H ) ) =>
if ( ord.lteq( x1, x2 ) )
RootQ( x1, RootedHeap.insert( ts2.asInstanceOf[RootQ], h1) )
else
RootQ( x2, RootedHeap.insert( ts1.asInstanceOf[RootQ], h2 ) )
}
override def findMin( ts: H ) = ts match {
case Empty => throw new NoSuchElementException("min of empty heap")
case RootQ( x, h ) => x
}
override def deleteMin( ts: H ) = ts match {
case Empty => throw new NoSuchElementException("delete min of empty heap")
case RootQ( x, h ) =>
if ( RootedHeap.isEmpty( h ) )
Empty
else {
val RootQ( y, h1 ) = RootedHeap.findMin( h )
val h2 = RootedHeap.deleteMin( h )
RootQ( y, RootedHeap.meld( h1, h2 ) )
}
}
}
测试:
测试Int类型:
object Test {
def main(args: Array[String]): Unit = {
//这里新建一个元素类型是Int的bootstrap堆
val heap = new BootstrapSkewBinomialHeap with IntHeap
//依次插入元素,其实认真观察,发现和传统的数据结构相比,
//每次操作之后原来的版本和新的版本同时存在,并不想传统的数据结构,
//更新操作之后,原来的版本就找不回来了。
val heap1 = heap.insert(1, heap.empty)
val heap2 = heap.insert(10, heap1)
val heap3 = heap.insert(-1, heap2)
val heap4 = heap.insert(-11, heap3)
val heap5 = heap.insert(3, heap4)
val heap6 = heap.insert(2, heap5)
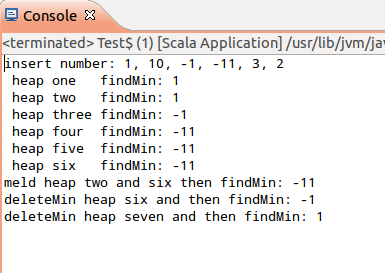
println(s"insert number: 1, 10, -1, -11, 3, 2")
println(s" heap one findMin: ${heap.findMin(heap1)}")
println(s" heap two findMin: ${heap.findMin(heap2)}")
println(s" heap three findMin: ${heap.findMin(heap3)}")
println(s" heap four findMin: ${heap.findMin(heap4)}")
println(s" heap five findMin: ${heap.findMin(heap5)}")
println(s" heap six findMin: ${heap.findMin(heap6)}")
val meldheap26 = heap.meld(heap2, heap6)
println(s"meld heap two and six then findMin: ${heap.findMin(heap6)}")
val heap7 = heap.deleteMin(heap6)
println(s"deleteMin heap six and then findMin: ${heap.findMin(heap7)}")
val heap8 = heap.deleteMin(heap7)
println(s"deleteMin heap seven and then findMin: ${heap.findMin(heap8)}")
}
}
结果:
换String元素类型测试:
object Test {
trait StringHeap extends Heap {
override type A = String
override def ord = scala.math.Ordering.String
}
def main(args: Array[String]): Unit = {
//元素类型是String的bootstrap堆
val heap = new BootstrapSkewBinomialHeap with StringHeap
val heap1 = heap.insert("my", heap.empty)
val heap2 = heap.insert("name", heap1)
val heap3 = heap.insert("is", heap2)
val heap4 = heap.insert("ldpe2g", heap3)
val heap5 = heap.insert("hexie", heap4)
val heap6 = heap.insert("fake", heap5)
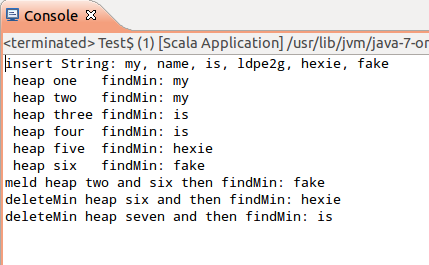
println(s"insert String: my, name, is, ldpe2g, hexie, fake")
println(s" heap one findMin: ${heap.findMin(heap1)}")
println(s" heap two findMin: ${heap.findMin(heap2)}")
println(s" heap three findMin: ${heap.findMin(heap3)}")
println(s" heap four findMin: ${heap.findMin(heap4)}")
println(s" heap five findMin: ${heap.findMin(heap5)}")
println(s" heap six findMin: ${heap.findMin(heap6)}")
val meldheap26 = heap.meld(heap2, heap6)
println(s"meld heap two and six then findMin: ${heap.findMin(heap6)}")
val heap7 = heap.deleteMin(heap6)
println(s"deleteMin heap six and then findMin: ${heap.findMin(heap7)}")
val heap8 = heap.deleteMin(heap7)
println(s"deleteMin heap seven and then findMin: ${heap.findMin(heap8)}")
}
}
结果: