R语言 参数估计 学习笔记
1.极大似然法的例子
在没学习统计之前，我估计也这么做。学完统计要绕好大一圈，结果还是一样的，真是作死啊。
2. R软件如何求方程的解。
2.1这还是个最大似然法求参数估计的例子。不同的是，要解导数为0 的方程并不容易。所以利用了R软件，迭代求解。
首先这个题目已经给出了分布，没给数据。我们先模拟一些数据出来：
#产生1000个θ=1的rcauchy分布下的随机数。
x <- rcauchy(1000,1);
#然后写出方程 所对应的函数 我们要求的是p。
f <- function(p){sum((x-p)/(1+(x-p)^2))}
out <- uniroot(f,c(0,5)) #uniroot是用来求一元方程解的函数，默认迭代1000次
> out
$root #近似解
[1] 1.017767
$f.root #那个地方的函数值
[1] -4.68199e-06
$iter #迭代次数
[1] 6
$estim.prec #误差估计
[1] 6.103516e-05
2.2 如果不求根，直接求似然函数的极大值点？
2.21 在一元的情况下，可以使用optimize(),optimise()求极点. 默认参数maximum = FALSE，是求极小值点。延续上面的例子
f <- function(p){sum(log(1+(x-p)^2))}
out <- optimize(f,c(0,5))
> out
$minimum #近似解
[1] 1.017747
$objective #函数值
[1] 1434.194
2.22 在未知数就一个的情况下使用optimize() , 未知数有多个的情况下应该使用nlm();
例：求f(x) = 100(x2 − x1^2)^2 + (1 − x1)^2在 （-1.2，1）区间上的极值点。
f <- function(x){100*(x[2] - x[1]^2)^2 + (1-x[1])^2}
nlm(f,c(-1.2,1))
$minimum #最优目标值
[1] 3.973766e-12
$estimate #最优点估计
[1] 0.999998 0.999996
$gradient #最优点处目标函数梯度值
[1] -6.539281e-07 3.335999e-07
$code #指标 为1则表示成功
[1] 1
$iterations
[1] 23
#上面函数有更好的写法
f <- function(x){
temp <- c(10*(x[2]-x[1]),(1-x[1]))
sum(temp^2)
}
3.正态总体的估计
3.1 正态中体的均值估计。
参照上面的统计原理，照着书编写R程序：
myMean.test <- function(x,sigma=-1,alpha=0.05){
n <- length(x); m <- mean(x)
if(sigma>=0){
tmp <- sigma/sqrt(n)*qnorm(1-alpha/2); df <- n;
}else{
tmp <- sd(x)/sqrt(n)*qt(1-alpha/2,n-1); df <- n-1;
}
data.frame("mean"=m,"df"=df,"L"=m-tmp,"G"=m+tmp);
}
df为自由度。因为R中q系列的函数求的都是下分位点，所以数学表达式中的上分为点写成1-alpha/2
例：工厂的零件长度服从正态分布N（u,0.04). 抽的样本 x <- c(14.6,15.1,14.9,14.8,15.2,15.1) 。求均值的95%的置信区间。
> source("E:\\hutao\\learning\\rscript\\myR.R")
> x <- c(14.6,15.1,14.9,14.8,15.2,15.1)
> myMean.test(x,0.2)
mean df L G
1 14.95 6 14.78997 15.11003
例：只知道是正态分布。抽了10次。
> x <- c(10.1, 10, 9.8, 10.5, 9.7, 10.1, 9.9, 10.2, 10.3, 9.9) > myMean.test(x) mean df L G 1 10.05 9 9.877225 10.22278
在R软件中 ，我们一般使用t.test()函数来做标准正态分布的均值检验 同上个例子。
> t.test(x) One Sample t-test data: x t = 131.5854, df = 9, p-value = 4.296e-16 alternative hypothesis: true mean is not equal to 0 #这里是备择假设 如果p值小于0.05 就接受这个假设 #否则接受假设H0，这里假设均值为0，我们不接受。 95 percent confidence interval: 9.877225 10.222775 sample estimates: mean of x 10.05
t.test()还能做很多检验。这里先就检验均值。
3.2正态分布的方差估计
照书搬运代码：
myVar.test <- function(x, mu=Inf, alpha=0.05){
n<-length(x)
if (mu<Inf){
S2 <- sum((x-mu)^2)/n; df <- n
}else{
S2 <- var(x); df <- n-1
}
a<-df*S2/qchisq(1-alpha/2,df)
b<-df*S2/qchisq(alpha/2,df)
data.frame(var=S2, df=df, "L"=a, "G"=b)
}
3.3 两个正态分布的均值差的区间估计
3.3.1先有一种，两个样本量的大小不一样，我只需要均值1-均值2的区间估计
在这样的情况下，又分三种情况。
1.两个总体的方差都知道。这个比较好理解，两个正态分布加减，还是一个正态分布。
2，3两种情况，我们只知道方差相等或者不相等，而不知道具体的值。
根据上述原理，搬运代码：
myMean.test2 <- function(x, y,sigma=c(-1,-1), var.equal=FALSE, alpha=0.05){
n1 <- length(x); n2 <- length(y)
xb <- mean(x); yb <- mean(y)
if (all(sigma>=0)){
tmp <- qnorm(1-alpha/2)*sqrt(sigma[1]^2/n1+sigma[2]^2/n2)
df <- n1+n2
}else{
if (var.equal == TRUE){
Sw <- ((n1-1)*var(x)+(n2-1)*var(y))/(n1+n2-2)
tmp <- sqrt(Sw*(1/n1+1/n2))*qt(1-alpha/2,n1+n2-2)
df <- n1+n2-2
}else{
S1 <- var(x); S2 <- var(y)
nu <- (S1/n1+S2/n2)^2/(S1^2/n1^2/(n1-1)+S2^2/n2^2/(n2-1))
tmp <- qt(1-alpha/2, nu)*sqrt(S1/n1+S2/n2)
df <- nu
}
}
data.frame("mean"=xb-yb, "df"=df, "L"=xb-yb-tmp, "G"=xb-yb+tmp)
}
这个函数的用法就不举例了。方差已知：myMean.test2(x,y,sigma=c(sigma1,sigma2)) 方差未知且相同myMean.test2(x,y,var.equal=T) 。在R语言中 ，t.test()也可以完成这样的检验。用法是相同的，不过好像没有sigma已知的检验。使用t.test()同时可以求出p值，并且可以做单侧检验。
3.3.2. 我们要用样本来比较两个总体的均值 ，但样本是成对出现的。比如超市两种品牌的泡面每天的销量，我总是能同时获得两个数据。这种配对数据的区间估计，将两组数据相减就变成单个样本了。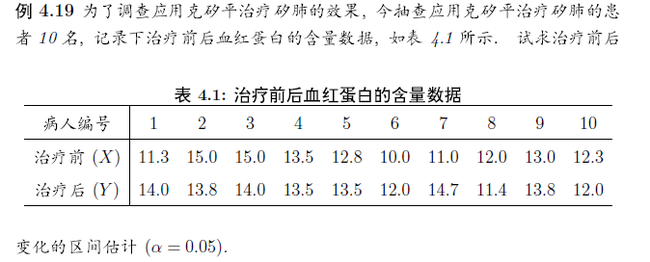
> x <- c(11.3, 15.0, 15.0, 13.5, 12.8, 10.0, 11.0, 12.0, 13.0, 12.3) > y <- c(14.0, 13.8, 14.0, 13.5, 13.5, 12.0, 14.7, 11.4, 13.8, 12.0) > t.test(x-y) One Sample t-test data: x - y t = -1.3066, df = 9, p-value = 0.2237 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: -1.8572881 0.4972881 sample estimates: mean of x -0.68 #p值高，置信区间包含0 所以不能说治疗有效果。
3.4 方差比的估计。
myVar.test2 <- function(x,y,mu=c(Inf, Inf), alpha=0.05){
n1 <- length(x); n2 <- length(y)
if(all(mu<Inf)){
Sx2 <- 1/n1*sum((x-mu[1])^2); Sy2 <- 1/n2*sum((y-mu[2])^2)
df1 <- n1; df2 <- n2
}else{
Sx2 <- var(x); Sy2 <- var(y); df1 <- n1-1; df2 <- n2-1
}
r <- Sx2/Sy2
a <- r/qf(1-alpha/2,df1,df2)
b <- r/qf(alpha/2,df1,df2)
data.frame("rate"=r, "df1"=df1, "df2"=df2, "L"=a, "G"=b)
}
在R语言中，var.test(x,y) 是用来做双样本方差比的区间估计的。
4.非正态总体的均值估计
当总体为非正态分布时，中心极限定理可知，只要样本容量充分大（一般习惯上要求 
）， 
的抽样分布近似服从正态分布。
当 
已知时，仍可用公式 
近似求出总体均值 
的置信区间；
当 
未知时，只要将公式 
中的总体标准差 
用样本标准差 
代替，就可近似得到总体均值 
的置信区间：
例 6.4 为了解居民用于服装消费的支出情况，随机抽取90户居民组成一个简单随机样本，计算得样本均值为810元，样本标准差为85元，试建立该地区每户居民平均用于服装消费支出的95%的置信区间。
解 假设用随机变量 
表示居民的服装消费支出，本题虽然总体分布未知，但由于 
，是大样本且 
未知，所以可利用公式 
近似得到总体均值 
的置信区间。根据题意， 
元， 
元， 
，与置信度95%相对应的 
，查标准正态分布表，得到 
。将这些数据代入公式 
，便可得到总体均值 
的置信度为95%的置信区间为
于是，我们有95%的把握认为，该地区每户居民平均用于服装消费的支出大约介于 
元到 
元之间。
myMean.test3 <-function(x,sigma=-1,alpha=0.05){
n <- length(x); xb <- mean(x)
if(sigma>=0){
tmp <- sigma/sqrt(n)*qnorm(1-alpha/2)
}else{
tmp <- sd(x)/sqrt(n)*qnorm(1-alpha/2)
}
data.frame(mean=xb, a=xb-tmp, b=xb+tmp)
}
5.单侧区间估计。在原理上 其实和双侧的差不多。所以懒得再复习一遍。可以将上面的双侧估计都改一改 我就不重新敲一遍了
5.1 均值估计
myMean.test3 <- function(x, sigma=-1, side=0, alpha=0.05){
n<-length(x); xb<-mean(x)
if (sigma>=0){
if (side<0){
tmp<-sigma/sqrt(n)*qnorm(1-alpha)
a <- -Inf; b <- xb+tmp
}else if (side>0){
tmp<-sigma/sqrt(n)*qnorm(1-alpha)
a <- xb-tmp; b <- Inf
}else{
tmp <- sigma/sqrt(n)*qnorm(1-alpha/2)
a <- xb-tmp; b <- xb+tmp
}
df<-n
}else{
if (side<0){
tmp <- sd(x)/sqrt(n)*qt(1-alpha,n-1)
a <- -Inf; b <- xb+tmp
}else if (side>0){
tmp <- sd(x)/sqrt(n)*qt(1-alpha,n-1)
a <- xb-tmp; b <- Inf
}else{
tmp <- sd(x)/sqrt(n)*qt(1-alpha/2,n-1)
a <- xb-tmp; b <- xb+tmp
}
df<-n-1
}
data.frame("mean"=xb, "df"=df, "L"=a, "G"=b)
}
R软件中，t.test(), var.test() 都可以选择做单侧还是双侧。
例：从一批灯泡中抽取5个做寿命测试。设灯泡寿命服从正态分布，求95%单侧置信下限。
解： 我们要有95%的把握 灯泡寿命大于某个数。因此，根据反证法的原理，原假设应该是小于某个数，备择假设是大于某个数。
> x <- c(1050, 1100, 1120, 1250, 1280) > t.test(X, alternative = "greater") #aleternative选项就是备择假设。 One Sample t-test data: x t = 26.0035, df = 4, p-value = 6.497e-06 alternative hypothesis: true mean is greater than 0 95 percent confidence interval: 1064.9 Inf sample estimates: mean of x 1160 #用刚刚编写的函数 效果一样 > myMean.test3(x,side=1) mean df L G 1 1160 4 1064.9 Inf
5.2 方差估计 下面是方差的改进版本
myVar.test3 <- function(x,mu=Inf,side=0,alpha=0.05){
n<-length(x)
if(mu<Inf){
S2<-sum((x-mu)^2)/n; df<-n
}else{
S2<-var(x); df<-n-1
}
if (side<0){
a <- 0
b <- df*S2/qchisq(alpha,df)
}else if (side>0){
a <- df*S2/qchisq(1-alpha,df)
b <- Inf
}else{
a<-df*S2/qchisq(1-alpha/2,df)
b<-df*S2/qchisq(alpha/2,df)
}
data.frame("var"=S2, "df"=df, "L"=a, "G"=b)
}
5.3，5.4 两个样本求均值差，求方差比 。这个程序就不写了 去书上翻好了。在R软件中 同样是 t.test(alternative="")和var.test(alternative="");