利用有限自动机(finite automata)进行模式匹配
一、一、有限自动机定义及基本术语:
一个有限自动机 M 是一个5元组(Q, q0,A, Σ, δ),其中:
Q 是所有状态的有限集合;
q0 ∈ Q (属于)是初始状态;
A ⊆ Q (子集)是接受状态的集合;(对应于多模式?)
Σ 是有限输入字母表;
δ 是从Q * Σ的转移函数,称为有限自动机M的转移函数;
记号与术语:
Σ* 表示用字母表Σ中所有字符形成的所有有限长度的字符串集合.
n 输入字符串(input string)的长度.
m 模式字符串(pattern string)的长度;也称作终态m,当状态为m时表示,m长度的模式串匹配成功.
|x| : 字符串x的长度, 如示符号记法.
![]() : 字符串w 是字符串x 的后缀,如示符号记法.(注意前缀/后缀均遵循传递规则)
: 字符串w 是字符串x 的后缀,如示符号记法.(注意前缀/后缀均遵循传递规则)
ε:表示空字符串,是所有字符串的后缀,前缀. (ε读作 epsilon )
a : 下文中的字符a泛指所有字符(a∈Σ),不特指字符'a'.
二、引入的函数定义:
转移函数δ(transition function) ( δ 读作"delta",对应大写为 Δ )
有限自动机开始于初始状态q0,每次读入输入字符串的一个字符,如果有限自动机在状态q是读入字符'a',
则M状态从q变成 δ(q, a);
终态函数 Φ(finite state function) ( Φ 读作"fai", 对应小写为 φ )
是从 Σ* 到 Q 的函数,Φ(w)是永动机M 扫描字符串 w 终止后的状态;M 接受字符串w 当且仅当Φ(w)∈A, 函数Φ有下列递归关系定义:
φ(ε) = q0;(空字符串 ε 的终态为q0)
φ(wa) = δ(φ(w),a) (其中w∈Σ*,a∈Σ)
辅助函数,后缀函数σ 对应于模式字串P ( σ 读作 "sigma", 对应大写为 Σ )
是从Σ* 到{0,1, ..., m}上的映射,σ(x)是字符串x的后缀同时是P的前缀的最大长度;
σ(x) = max{k: Pk ⊐ x }
有P0 = ε是所有所有字符串的后缀;
* 后缀函数的主要意义的是求出当前匹配失败时,求出已经匹配过的部分字串x是否是待匹配模式字串P的前缀,即匹配可以跳过x中部分长度( σ(x) ),可以用于实现转移过程;同时也表明在接受输入字符串x后的状态(终态),即也用于实现终态函数。
三、字符串匹配自动机(string-matching automation)
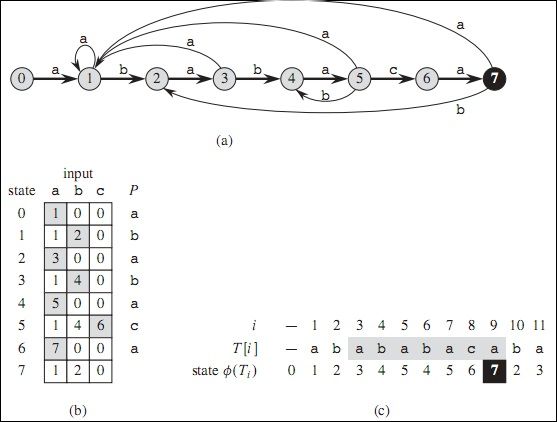
下图是依据模式串 P="ababaca" 构建的自动机图表:
上图(a)是一个自动机的状态转换图表,接受所有以字符串"ababaca"结尾的字符串。其中状态0是初始状态,状态7是唯一接受状态(单模式匹配).
1) 从状态i到状态j的带箭头的有向边表示转移过程: δ(i, a) = j(a∈Σ).
2) 右向边组成了自动机的主要"骨架",图中粗线部分,对应于输入字符同模式字串匹配成功的转移过程。左向边对应于匹配失败的转移过程(跳转,主要是计算已经匹配的部分字串 的后缀子串同时是模式串P的前缀的最大长度).部分匹配失败的过程没有标示出来。
3) 图中部分状态i在接受某字符a(a∈Σ)时,没有标示出对应有向边的情况表明其转移过程为: δ(i, a) = 0(a∈Σ),根据下面字符串模式匹配自动机定义,知当前已经匹配子串没有后缀字串是模式串P的前缀。如在状态3时,输入字符为'c',即在已经匹配了"aba"这时接受字符'c',知当前已匹配字串为"abac",对应模式字串P="ababaca",可知这时匹配失败,进行失败跳转求"abac"后缀子串同时是模式串P前缀的最大长度,可知为0.
4) 匹配成功的转移过程(对应状态,以及对应输入字符)均标示为灰色,
5) 表(c)是自动机在处理(接受)输入文本T="abababacaba"的最终状态表。当输入字符T[i]时,此时字串T[0...i]对应的的最终状态φ(T[0...i]) 同表(c)最后一列一一对应。有T["abababaca"] = P.length = 7(唯一接受状态),即这时候在T串中匹配成功模式串P,结束位置为9,起始位置为(9-P.length+1)=3。
1、字符串匹配有限自动机定义:
给定模式(pattern)字符串 P[1...m],其对应的字符串匹配有限自动机定义如下:
1、状态集Q = {0,1,...m},开始状态q0 是状态0,state m 是唯一的接受状态;
2、转移函数δ 可以用后缀函数来表示 (这个很重要, 因为状态转移函数是个抽象概念,而后缀函数可以用code表示) :
δ(q,a) = σ(Pq,a) <等式一>
假设当前已经读入的字符串为T,为了让T的字串(以T[i]为结尾) 能匹配模式字串Pj,必须满足Pj是Ti的后缀;同时假设q = φ(Ti),说明读取字串Ti后自动机M 状态变成q;同时根据转移函数<等式一>可知q是模式字串P最大长度的前缀,同时是Ti的后缀;因此在状态q,有Pq ⊐ Ti 和 q = σ(Ti) (当q 等于m 时,说明模式字串P整个是Ti的后缀,也意味着匹配查找成功了),因此有σ(Ti)= q,得出永动机也支持下面的等式(终态函数也是抽象的,转化为后缀函数表达式后,可以用code表示):
φ(Ti) = σ(Ti)(i = 0,1,...n) <等式二>
2、同时有两个引理(具体证明可以参考算法导论):
引理1、后缀函数不等式:
σ(xa) ≤ σ(x) + 1 (对于任何字符串x,以及字母a)
引理2、后缀函数递归引理:
对于任何字符串x,以及字母a,如果q = σ(x),有:
σ(xa) = σ(Pqa)
<等式二> 可以用数学归纳法证明,具体如下:
1、当i = 0,因为T0 = ε,因此有φ(Ti) = 0 = σ(Ti)
2、假设φ(Ti) = σ(Ti),证明φ(Ti+1) = σ(Ti+1),用q 表示φ(Ti),用字母a表示T[i+1],有:
φ(Ti+1) = φ(Tia) (Ti+1 == Tia)
= δ(φ(Ti),a) (根据终态函数的定义)
= δ(q,a) (根据q的定义)
= σ(Pqa) (根据等式一)
= σ(Tia) (根据引理二)
= σ(Ti+1) (Ti+1 == Tia)
从上面可以知道当读入T i 的终态(亦即读入T[i]后转移函数状态)等于模式长度,就匹配成功了,下面是有限自动机机匹配算法伪代码:
下面就是根据<等式一>来实现转移函数的伪代码:
下面是我自己实现的code:
#include <iostream>
#include <string.h>
using namespace std;
#define MIN(X,Y) ((X)<=(Y) ? (X) : (Y))
#define MAX_NEEDLE_LEN 0xFF
#define MAX_ALPHABET_NUM 0XFF
/*
check if needle[0~k-1] is suffix of needle[0~q-1 'ch']
*/
int is_suffix(const char * needle, int k, int q, unsigned char ch)
{
int i = 0;
int suffix_len = k;
if(NULL == needle || suffix_len < 0 || suffix_len > 7)
{
return -1;
}
if(needle[suffix_len - 1] != ch)
{
return -1;
}
if(1 == suffix_len)
{
return 0;
}
for(i=0; (suffix_len > 1)&&(i < suffix_len) && (i < q); i++)
{
if(needle[suffix_len - 2 - i] != needle[q - 1 - i])
{
break;
}
}
if(i >= q)
{
return 0;
}
return -1;
}
unsigned int delta[MAX_NEEDLE_LEN][MAX_ALPHABET_NUM] = {0};
void compute_transition_func(const char *haystack, const char *needle)
{
int q = 0, k = 0, j = 0;
int n = strlen(haystack);
int m = strlen(needle);
for(q = 0; q < m; q++)
{
for(j = 0; j < n; j++)
{
k = MIN(m+1,q+2);
do
{
k--;
if(0 == is_suffix(needle, k, q, haystack[j]))
{
break;
}
}while(k > 0);
delta[q][haystack[j]] = k;
}
}
}
void finite_automaton_matcher(const char *haystack, const char *needle)
{
unsigned int n = strlen(haystack);
unsigned int m = strlen(needle);
int q = 0, i =0, j = 0;
int reCheck_Pos_array[0xff] = {0};
unsigned int reCheck_Index = 0;
unsigned need_reCheck = 0;
unsigned reOccurence = 0;
if(needle[0] == needle[1])
{
need_reCheck = 1;
}
for(i = 0; i< n; i++)
{
//printf("q=[%d], haystack[%d]=[%c] delta[%d][%c]=[%d]\n", q, i, haystack[i], q, haystack[i], delta[q][haystack[i]]);
q = delta[q][haystack[i]];
if(q == m)
{
printf("\nSuccess find at haystack[%d] !\n", i-m+1);
}
if(needle[0] == haystack[i])
{
reOccurence++;
if(reOccurence >=2)
reCheck_Pos_array[reCheck_Index++] = i-1;
}
else
{
reOccurence = 0;
}
}
if(0 == need_reCheck)
return;
printf("Need recheck ,and reCheck times [%d]\n", reCheck_Index);
for(i = 0; i< reCheck_Index; i++)
{
q = 0;
for(j = 0; j< m; j++)
{
//printf("q=[%d], haystack[%d]=[%c] delta[%d][%c]=[%d]\n", q, reCheck_Pos_array[i] + j, haystack[reCheck_Pos_array[i] + j], q, haystack[reCheck_Pos_array[i] + j], delta[q][haystack[reCheck_Pos_array[i] + j]]);
q = delta[q][ haystack[ reCheck_Pos_array[i] + j ] ];
if(q == m)
{
printf("Recheck RSuccess find at haystack[%d] !\n", reCheck_Pos_array[i]);
}
}
}
}
void main()
{
char needle[] = "aabab";
char haystack[] = "aaababaabaababaab";
//compute delta
compute_transition_func((const char *)haystack, (const char *)needle);
finite_automaton_matcher((const char *)haystack, (const char *)needle);
}
后面在测试的时候,发现在“aaababaabaababaab”里面查找“aabab”会有遗漏,大家可以debug看下,我针对这种情况作了处理,部分要回过头重复检查, 会影响效率,没想到好方法,欢迎大家指点~~
ps : 2014-08-06日,自己回顾下有限自动机,发现部分错漏,自己重新看了遍算法导论,修正了一遍,以此记录。通过回顾,自己归纳下字符串匹配自动机主要是在某个字符匹配失败时,利用已知匹配失败的部分,看是否有部分是模式串P的前缀,以便跳过部分以节省时间。关键是后缀函数的理解, 当然后面几篇模式匹配算法也有用到其他方法,也有几种方法结合的,具体要看业务需要。
参考:
1、《Introduction to algorithms》