计算机是如何做加法的?(6)——最终的半加器
在上一篇,我们谈到了进制的问题,如果用二进制的话,加法表只有四条规则:
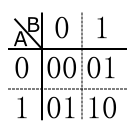
0+0=00,
0+1=01,
1+0=01,
1+1=10
以此为需求,再次尝试构建半加器。
分解
首先,大的结构还是稳定不变的:
这点不会因为采用不同的进制而有所不同。
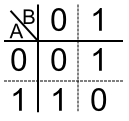
把上述四种情况,一横一坚弄成一张表,如下:
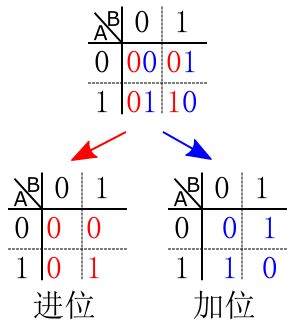
再按加位和进位分成两部分,如下:
进位器
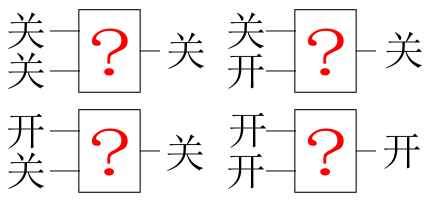
先考虑进位的情况。根据上表,进位器它要满足以下几种情况:
跟之前类似,令“关=0,开=1”,那么
用一句话来概括就是:“两个都是开,结果才是开,任意一个没开,结果就是关。”
你还记得有什么电路有如此的性质呢?
串联电路
还记得串联电路不?
注:由来自《编码:隐匿在计算机软硬件背后的语言》(Code: The Hidden Language of Computer Hardware and Software)一书中的图片整合而成。下面类似的截图或来自此书,或参考原书中的例图画成。
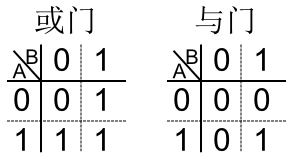
与门
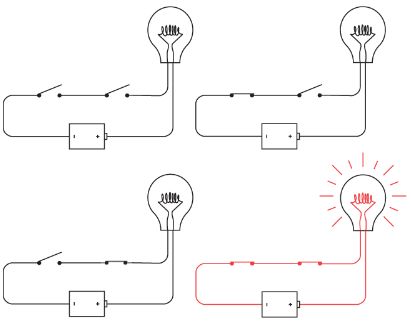
那么,当以串联的方式连接两个继电器时:
这样的一个东西就是所谓的与门(And Gate)了,如果用一个符号”&”来表示一个与操作,把0和1想像成上面的关和开,那么
0 & 0 –> 0
0 & 1 –> 0
1 & 0 –> 0
1 & 1 –> 1
与门用以下符号来表示,它有两个输入一个输出:
它实际是对这样一种功能的抽象:
与门满足以下逻辑:
那么,这也正是进位器要表达的逻辑。对半加器而言,所谓进位器,就是一个与门,因此到目前为止我们的半加器是这样的:
接下来再来看加位器的设计。
加位器
加位器的逻辑是这样的:
到目前为止,我们已经有了或门和与门,它们的逻辑如下:
很遗憾,现有这些门的逻辑都不符合要求。
当然我们也不难注意到或门已经很接近加位器的逻辑了,除了右下角有些出入外:
而且我们特别注意到,对加位器而言,当两个输入为1时输出反而是0.(1+1会导致进位从而使得加位归零)
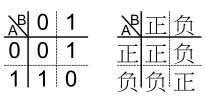
观察加位器的逻辑,如果把0和1看成是正和负,倒是有点像我们所说的“负负得正”的情况:
但显然,无论是对于并联(或门)还是串联(与门)电路,是不可能存在什么“负负得正”的,当输入都为1时,灯泡没理由不亮。
想要达到输入都为1时,输出反而为0,或门和与门都不可能满足要求,这里我们需要一点“反向”的思维。
反向器,非门
在之前,继电器的开关缺省都是处于断开的状态,但这一点并不是必须的,我们也完全可以让它缺省处于打开的状态:
显然,把灯泡接在上面一个触点上就行了。
那么对于第二种情况,当有输入时,开关反而被吸引下来导致电路断开:
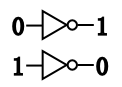
那么这样一种电路我们称之为反向器(Inverter),又称之为非门(Not Gate),用以下的符号表示:
它只有一个输入,一个输出。它是对这样一个功能的抽象:
它能表达以下逻辑:
或非门
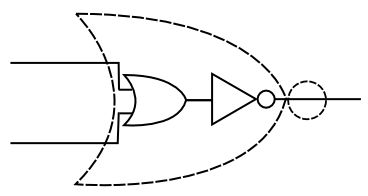
当把或门的输出又接在一个非门上时,或门的输出都被取反:
通过这么一个反向,我们可以在右下角也得到输出为0的情况了,但这么一来,其它三个原本OK的逻辑现在反而又不行了。
正所谓“按下葫芦起了瓢”。
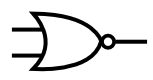
这样一种组合我们称之为“或非门(Not Or Gate,又称为Nor Gate)”,用以下符号表示:
它是对以下组合的一种抽象:
当然它不能满足加位器的要求,我们可以再试试其它的组合。
与非门
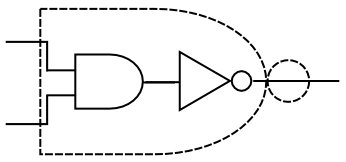
同理当把与门的输出又接在一个非门上时,与门的输出都被取反:
这一次,对比加位器的要求,右下角OK了,但左上角又不行了。
这样的一种组合,我们称之为与非门(Not And Gate,或Nand Gate)。用以下符号表示:
它是对以下组合的一种抽象:
显然,与非门还是差了一点点从而无法满足加位器的要求。
异或门
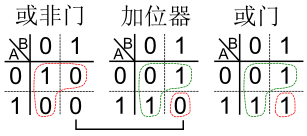
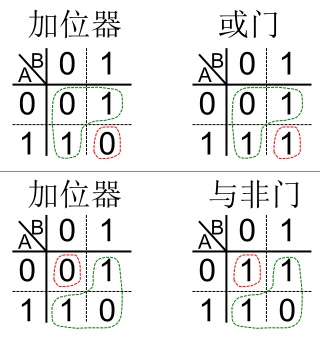
如果观察与非门以及之前的或门与加位器之间的逻辑:
显然,它们各自覆盖了加位器逻辑的一大部分,如果它们能够以某种方式再次组合起来,是不是能全面覆盖加位器的逻辑呢?
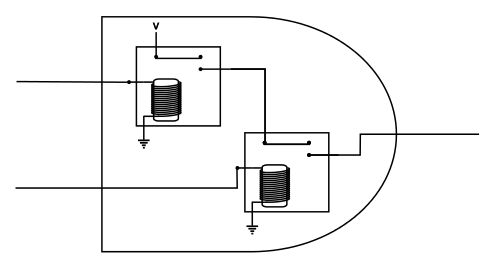
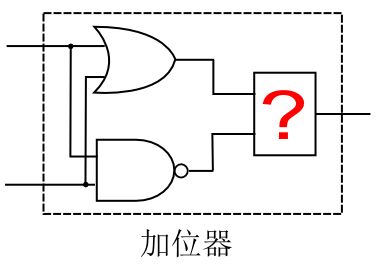
换句话说,我们希望在两者基础之上再去综合,也即考虑如下的加位器内部结构:
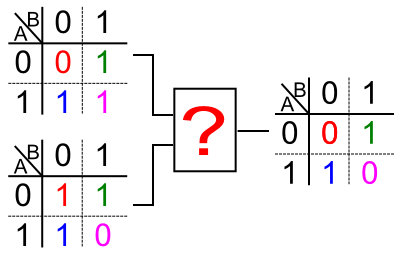
对于图中未知的部件,它要满足以下逻辑:
它接受前述或门和与非门的输入,并产生最终的进位器输出。
一一分解四种情况,并对比现有的四种两个输入一个输出的门电路
那么不难发现,或门跟与门均能满足上图中蓝色部分的要求,而与门跟或非门都能满足图中紫色部分的要求,只有与门是它们的交集,也即能满足所有四种情况。所以这里的未知部件可以用一个与门代替。
可能有人会问你为何就要这样去划分上图中的两部分呢?的确,这有点事后诸葛亮的味道,实际中我们确实是需要一定的尝试,才能最终找到正确结果,另外我们也要对门电路的逻辑特性非常熟悉才行。应该说我们的运气还是不错的,这里只需要一个简单的门电路就OK了,更复杂的情况我们可能需要继续组合多个门电路才能达到要求。
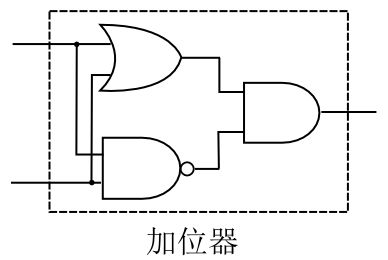
至此,我们得到了加位器的结构如下:
当然了,实际上没有加位器这种叫法,这样一个东西就叫“异或门(Xor Gate)”。
Xor Gate: Exclusive Or Gate,这里强调了它与“或门”的联系及区别。
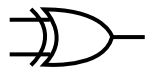
它用这样的符号去表示:
这个图也体现了它跟或门的渊源。
它是对以下组合的抽象:
尽管异或门跟或门的输出仅仅有一个地方不同,但最终结构上两者相差是很大的,异或门要复杂得多,更不用说异或门内部就包含一个或门。
半加器
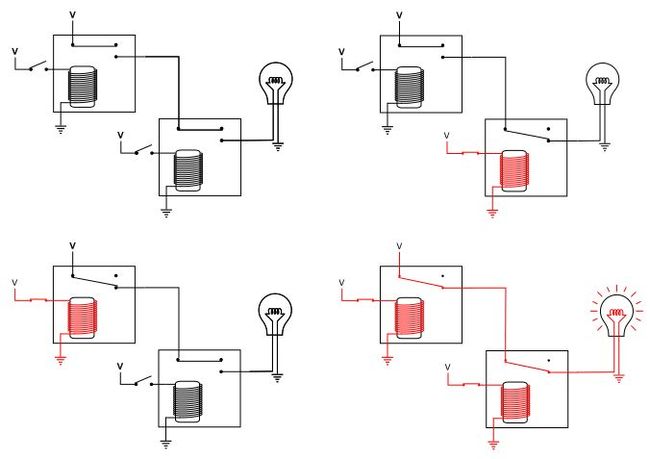
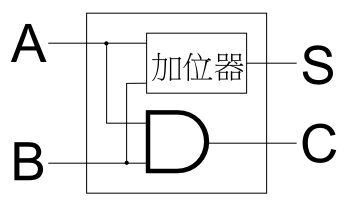
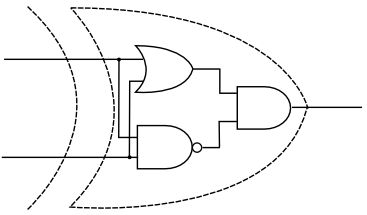
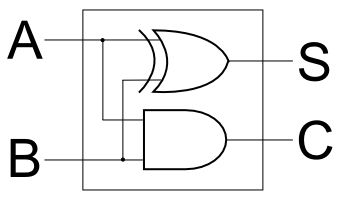
那么,我们最终的半加器的结构是这样的:
它由一个异或门和一个与门构成,分别负责加位与进位的输出,这就是最终的二进制半加器。
在下一篇,我们再做些回顾与总结。