POJ 1151 Atlantis 线段树+扫描线+离散化+延迟更新

POJ 1151 最先用矩形分割过了，然后才开始研究扫描线。说实话扫描线确实是一个比较巧妙的思路，但网上讲解扫描线的也比较少……

贴个连接(这片博文引导我理解了扫描线)：http://www.cnblogs.com/ka200812/archive/2011/11/13/2247064.html

PS:吐槽一句，这题的坐标搞得人真蛋疼，实际上应该是原点在左上角的（向右的x轴与向下的y轴）笛卡尔坐标系(实际上就是图形坐标系)，题目输入为(top，left，bottom，right)的形式。博文中的看似坐标与题目描述不太一致，实际不影响结果。

大体上的思想就是，对y轴建立线段树，顺序扫描各个矩形竖边(相当于对矩形竖向切割)，在此过程中计算当前边与其左边的竖边围成的面积并求和就是最终的面积了……

当然这个过程是由很多细节需要考虑的！

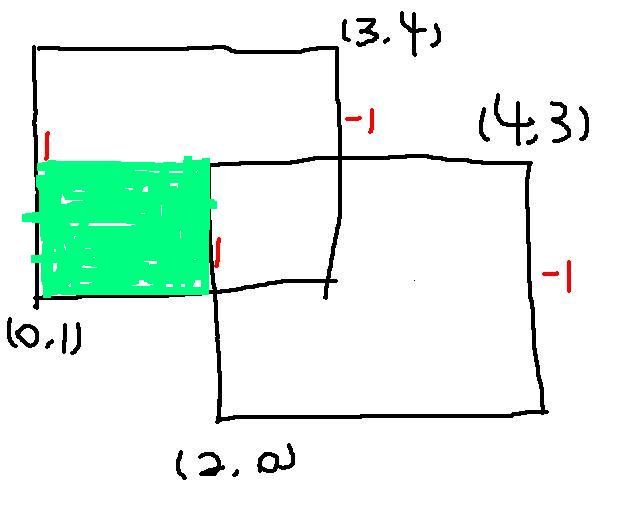如图，当扫描第一条竖线[1,4]时，区间[1,4]上暂时不存在线段。当扫描第二条竖线[0,3]时，第二条竖线与第二条竖线的公共部分[1,3]围成有效面积(途中绿色部分)，而区间[0,1]暂时不存在线段故没有围成有效面积。

于是我们想，对线段树每个节点(子区间)，标记当前区间之前覆盖的线段的x坐标，然后用当前扫描线的x坐标减去之前覆盖的线段的x坐标的差(围出有效面积的长)乘当前区间长度(宽)就能算出本次扫描出的有效面积。

但是又有一个问题，我们可以实时更新每个区间之前覆盖线段的x坐标，但是怎么更新？显然，若现在有线段[3,4]，显然不能和第三条竖线的[3,4]围成有效面积。因为第三条竖线是第一个矩形的右竖线，它的[3,4]部分已经和第一条竖线的[3,4]围出有效子矩形，不能在作为某个子矩形的左竖边去和某个右竖线围出矩形。这提示我们需要考虑每条竖线是原矩形的左竖边还是右竖边……

再看上面的图，观察四条竖线[1,3]部分的依次匹配，可以假想每条右边的匹配会消耗掉一条可匹配的左边(这个说法不太合理，只能这样想想，暂时想不到好的描述方法)。我们对每个区间计数，若有一条左竖边覆盖该区间就对边覆盖计数器count+1，一条右竖边覆盖区间就对覆盖计数器count-1。这样，当依次扫描竖线时，若匹配区间count>0则可围出有效面积，否则无法围出。依次统计即可。

我的代码中：

1).对y坐标进行离散化(对x还是对y具体看前面扫描的竖线还是横线)，解决了线段界值非整值或者离散度过大浪费空间的问题。离散化用map进行了实际值到离散值的映射，用vector进行了离散值到实际值的反映射。

2).对每个线段加上cover标记，进行延迟更新

切记：当搞清核心问题后，就是基本的线段树操作，离散化和懒惰标记。做好线段树节点状态值后，就可以抛开前面烦人的细节问题！

代码如下：

#include<iostream>
#include<cstdio>
#include<map>
#include<vector>
#include<iterator>
#include<algorithm>
using namespace std;

#define MAXN 101    //矩形数目+1        //左闭右开
#define lson LB,(LB+RB)>>1,num<<1    //左子节点
#define rson (LB+RB)>>1,RB,num<<1|1    //右子节点

map<double,int> MapInfo;    //正映射
vector<double> OpMap;    //逆映射

struct LN    //扫描线结构
{
    double x,top,bottom;
    int flag;
    bool operator<(const LN& a)const
    {return x<a.x;}
}Line[MAXN<<1];

struct    //线段树结构
{
    int count,pre;
    int cover;    //覆盖标志
}SegTree[MAXN<<3];

void BuildTree(int LB,int RB,int num)    //初始化线段树
{
    SegTree[num].count=0;
    SegTree[num].pre=0;
    SegTree[num].cover=1;
    if(LB+1!=RB)
    {
        BuildTree(lson);
        BuildTree(rson);
    }
}

void PushDown(int num)    //将当前节点的状态信息更新到子节点中
{
    int ls=num<<1,rs=num<<1|1;
    if(SegTree[num].cover==1)
    {
        SegTree[ls]=SegTree[rs]=SegTree[num];
        SegTree[num].cover=0;    //清除覆盖标记
    }
}

void PushUp(int num)    //将合并的子区间合并回写到父区间    
{                    //不要也可以，效果不是很明显
    int ls=num<<1,rs=num<<1|1;
    if(SegTree[num].cover==1) return ;
    if(SegTree[ls].cover!=1) return ;
    if(SegTree[ls].cover==SegTree[rs].cover&&SegTree[ls].count==SegTree[rs].count&&SegTree[ls].pre==SegTree[rs].pre)
        SegTree[num]=SegTree[ls];
}

double Insert(int k,int l,int r,int LB,int RB,int num)
{
    double area=0.0;
    if(l==LB&&r==RB)    // 区间匹配
    {
        if(SegTree[num].cover==1)    //区间完全覆盖一致
        {
            if(SegTree[num].count>0) //所覆盖线段count值>0，求当前线段和该区间上之前的线段围成的面积
                area+=(Line[k].x-Line[SegTree[num].pre].x)*(OpMap[r-1]-OpMap[l-1]);    //从0放入vector，故而-1
            SegTree[num].count+=Line[k].flag;    //修正覆盖计数器
            SegTree[num].pre=k;    //修正区间前驱线段
            SegTree[num].cover=1;    //修正区间覆盖标记
        }
        else    //区间状态不一致，子区间分别插入查询
        {
            int MID=(LB+RB)>>1;
            area+=Insert(k,l,MID,lson);
            area+=Insert(k,MID,r,rson);
            PushUp(num);
        }
    }
    else    //区间不匹配
    {
        PushDown(num);
        int MID=(LB+RB)>>1;
        if(r<=MID) area+=Insert(k,l,r,lson);
        else if(l>=MID) area+=Insert(k,l,r,rson);
        else
        {
            area+=Insert(k,l,MID,lson);
            area+=Insert(k,MID,r,rson);
        }
        PushUp(num);
    }
    return area;
}

int main(int argc,char* argv[])
{
    int i(0),k(1),N(0),m(1),n(1);
    double t,l,b,r,area;
    cin>>N;
    while(N)
    {
        m=0;area=0.0;    //清除状态值
        MapInfo.clear();    //清除容器
        OpMap.clear();
        for(i=0;i<N;i++)    //读入数据
        {
            cin>>t>>l>>b>>r;
            MapInfo.insert(pair<double,int>(t,0));    //纵坐标插入容器进行离散
            MapInfo.insert(pair<double,int>(b,0));    
            Line[++m].top=t;Line[m].bottom=b;Line[m].x=l;Line[m].flag=1;    //读入扫描线段
            Line[++m].top=t;Line[m].bottom=b;Line[m].x=r;Line[m].flag=-1;
        }
        BuildTree(1,m+1,1);    //m条线段，最多m个纵坐标，全线段[1,m+1)
        map<double,int>::iterator p;
        for(p=MapInfo.begin(),i=1;p!=MapInfo.end();p++,i++)    //完成离散化
        {
            p->second=i;    //映射排序后的离散值
            OpMap.push_back(p->first);    //建立反向索引一遍根据离散值获取实际值
        }
        sort(Line+1,Line+m+1);    //扫描线排序(从1开始放起，故而排序时+1)
        int lindex,rindex;
        for(i=1;i<=m;i++) //插入线段并求和面积
        {
            lindex=(MapInfo.find(Line[i].top))->second;        //线段离散化后的对应坐标
            rindex=(MapInfo.find(Line[i].bottom))->second;    //插入线段并求和面积
            area+=Insert(i,lindex,rindex,1,m+1,1);
        }
        cout<<"Test case #"<<k<<endl<<"Total explored area: ";
        printf("%.2f\n\n",area);
        cin>>N;k++;
    }
    return 0;
}