移动节点和AP网络优化

 

In Proc. of Networking 2005, Waterloo, Canada, May 2005

Measuring Round Trip Times to Determine

  the Distance between WLAN Nodes

Andr´ G¨ nther and Christian Hoeneeu

Telecommunication Networks Group (TKN), TU-Berlin, Germany

            [email protected]|[email protected]

Abstract. This publication explores the degree of accuracy to which

the propagation delay of WLAN packets can be measured using today’s

commercial, inexpensive equipment. The aim is to determine the distance

between two wireless nodes for location sensing applications. We con-

ducted experiments in which we measured the time difference between

sending a data packet and receiving the corresponding immediate ac-

knowledgement. We found the propagation delays correlate closely with

distance, having only a measurement error of a few meters. Furthermore,

they are more precise than received signal strength indications.

To overcome the low time resolution of the given hardware timers, various

statistical methods are applied, developed and analyzed. For example,

we take advantage of drifting clocks to determine propagation delays

that are forty times smaller than the clocks’ quantization resolution.

Our approach also determines the frequency offset between remote and

local crystal clocks.

1

Introduction

Knowing the position of wireless nodes is required for location-aware services

and applications. The position can be calculated using the distance between

wireless nodes. Furthermore distance helps when deciding the time of handovers

or finding the optimal routing path throughout an ad-hoc network.

    In this paper we focus on locating techniques which use the intrinsic fea-

tures of WIFI based wireless access. Usually, received signal strength indications

are applied to identify the location of wireless nodes. We show that precise dis-

tance measurement based on round trip time measurements of WLAN packets

is possible even with low-cost, commercial WLAN hardware. We developed the

algorithms to determine the air propagation time indirectly and to improve the

accuracy and resolution of the time measurements. We validated our approach

with two independent experimental measurement campaigns and with an ana-

lytical explanation.

    We utilize the following intrinsic feature of IEEE 802.11: Each unicast data

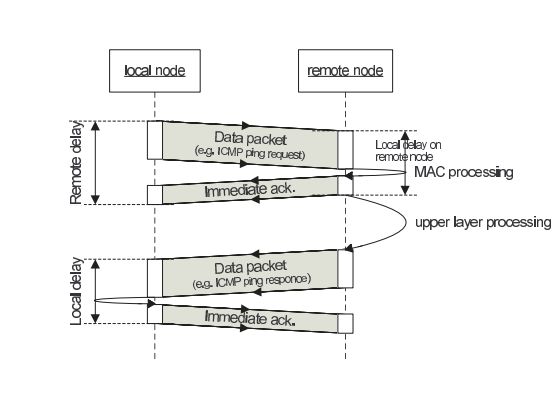
packet is immediately acknowledged by its receiver (Fig. 1). We took the time

This work has been supported by the Deutsche Forschungsgemeinschaft (DFG). This

publication is a condensed and enhanced version of [1]

between starting the transmission of a data packet and receiving the correspond-

ing immediate acknowledgement. We will refer to this as remote delay (dremote ).

We also measured the duration of receiving one data packet and sending out

the immediate acknowledgement. We will call this duration local delay (dlocal ).

The overall propagation time is then estimated by subtracting the local from

the remote delay.

c=

  2 · distance

                 where c ≈ 3 · 108 m being the speed of light.sdremote − dlocal

(1)

                                                      In order to overcome the

                                                  problem of interrupt laten-

                                                  cies and hence inaccuracies

                                                  when measuring the duration

                                                  of packet transmission in the

                                                  operating system, we mea-

                                                  sured the time on the hard-

                                                  ware layer - the WLAN card.

                                                  Most WLAN solutions allow

                                                  to record time stamps at a

                                                  resolution of 1 µs. However,

                                                  a packet travels a distance of

                                                  300 m in 1 µs, which usually

                                                  exceeds the range of WLAN

                                                  transmission. We increase the

Fig. 1. Distance measurement: Transmission of resolution by using multiple

                                                  delay observations and apply-an ICMP ping sequence.

                                                  ing statistical methods to en-

                                                  hance the accuracy.

    This paper is structured as follows: In Sect. 2 we refer to the state of the

art. Then we explain our approaches to enhance the measurement resolution. In

Sect. 4 we describe our experimental measurement campaigns. Finally, we briefly

summarize the results and contributions of this paper.

2

Related Work

A couple of approaches to in- and outdoor location sensing techniques have been

presented in [2]. An essential part of location sensing algorithms is a method to

determine the distance between two wireless nodes. In general, three methods

have been considered. Firstly, in case of densely populated networks such as

sensor networks [3] the information about which nodes are within transmission

range is used. Secondly, the received signal strength indication (RSSI) of data

packets transmitted is considered. It decreases sharply in a non-linear fashion

with distance, so that environment specific signal strength maps relating RSSI

values to positions have to be created first. An example for RSSI application is

2

the RADAR system [4], which has been one of the first approaches presenting

an indoor positioning system based on WLAN components (overview in [1]).

Thirdly, the propagation time of radio signals can be used because in free air it

linearly increases with distance. Such an approach is usually considered to be

impossible without the help of special signal processing hardware [5].

    The classic approach to the latter method of position location estimates the

time of arrival (TOA) of pure radio signals (instead of WLAN packets). This is

conducted by applying signal processing algorithms based on cross-correlation

techniques [6]. The TOA method suffers from multi-path conditions. This prob-

lem can be encountered with a wider frequency band, e.g. ultra-wide band.

    TOA measurement is being employed both outdoors for GPS-positioning [7]

and indoors to find things and people marked by a tag [8]. In the latter paper, the

author gives an appraisal of the achievable accuracy when measuring the round

trip TOA within the 2.44 GHz and 5.78 GHz bands. For a signal bandwidth of

40 MHz, the accuracy of 3.8 m can be an achievable resolution limit unless further

signal processing techniques are applied. Those might enhance the resolution up

to 1 m.

    The only paper focussing on measuring pure packet propagation delays is [9].

The objective is to determine the speed of light using the averaged measured

round trip propagation delay of ping packets. The measurements were con-

ducted in a wired Ethernet infrastructure. Estimating the propagation delay

which ranges below the clock resolution was facilitated by employing the con-

cept of noise-assisted sub-threshold signal detection. For measurements in an

IEEE 802.11b wireless environment the round trip times were too variable and

noisy to be used.

3

Approach

Inspired by the approach presented in [9] we also use the mean round trip time

delay of packets to determine the distance as given in (1). In order to keep the

time measurements as unbiased as possible resulting in a high resolution, we try

to preclude any disruption caused by operating system activities. To do so, we

took the following action:

    Firstly, we utilized the IEEE 802.11 data/acknowledgement sequence instead

of the ICMP-Ping request/response packet sequence. As the ping response is

generated by the operation system the time it takes is subject to a highly variable

delay. In contrast, the immediate acknowledgements are handled by the hardware

of the WLAN radio and hence highly predictable. As for our measurements we

assumed the MAC processing time to be equal on both wireless nodes. Although

the MAC processing time is standardized according to IEEE 802.11 we will prove

that not all WLAN cards operate in compliance with the standard. In practice,

the MAC processing time also depends on the chip set hardware and firmware

of the actual WLAN cards in use. To account for this a model-specific absolute

delay offset needs to be considered.

3

    Secondly, we do not measure the time stamps for packet arrival and trans-

mission on the operating system layer, but on the WLAN card hardware layer.

This features measuring conditions that are independent of variable interrupt

latencies. In [10] we showed that measuring the time of a packet’s arrival in

the operating system’s kernel (e.g. during an interrupt) entails quite imprecise

results due to falsification by the variable interrupt latency.

    The resolution of these hardware time stamps, which are implemented in

most current WLAN products, is 1 µs corresponding to 300 m. In terms of the

achievable accuracy this discrete time resolution is not precise enough yet. The

resolution increases when averaging numerous observations. In the following we

consider three phenomena that help to achieve a higher resolution.

Gaussian noise: The presence of measurement noise is assumed. Noise can be

caused by thermal noise in the received radio signal or by the presence of multi-

path environment. Also, the crystal clocks of the WLAN equipment are subject

to a constant clock drift and variable clock noise. Thus, the delay values are

not limited to only one value. (In Fig. 2 not only 323 µs can be observed but

also other values). If one assumes a Gaussian noise distribution with a suitable

strength, we can simply take the sample mean to enhance the resolution.

Stochastic Resonance: Instead of the explanation above the authors of [9]

suggested another statistic effect called stochastic resonance. The concept of

stochastic resonance was originally introduced as an explanation for the period-

ically recurrent ice ages. In the last two decades, it has been applied to explain

many physical phenomena [11]. In the realm of signal detecting stochastic res-

onance allows for detecting signals below the resolution of the measuring units

because the signal becomes detectable with the help of noise. Noise adds to the

signal so that it eventually exceeds the threshold given by the resolution of the

detecting device. Thus, the system is able to change its states. The state dura-

tions have random lengths, but the probability is high that one state remains

the same in the next observation.

Beat Frequencies: In our experiments (Fig. 4.3 in [1]) it can be observed that

the 323 and 324 values occur in blocks of regular patterns. But this effect cannot

be explained with the effect of stochastic resonance. Another effect can also

entail resolution enhancement even if measurement noise is missing: ’Relative

clock drift’ – both WLAN cards are driven by built-in crystal oscillators that

have nearly the same frequency. Due to tolerances, there is a slight drift between

both clocks which causes varying rounding errors.

    Let us consider the impact of a discrete time resolution on the measurement

error. Firstly, we construct a model of the experiment setups. Instead of using

packets, we assume that a delta pulse is sent off from the local to the remote node.

After the delta pulse’s arrival another delta pulse is sent back to the local node

representing an acknowledgement. The local node can only process the impulses

only in discrete time steps tlocal ∈ N described with natural numbers. The same

is also valid for the remote node. It only reacts in discrete time steps, which are

4

tremote = δ + n where n ∈ N and phase offset of δ ∈ [0; 1[. We assume that

the clocks work at the same speed but with a phase offset. Moreover, another

assumption is that phase offset changes over time but not for the duration of

a round trip. The transmission of a delta impulse from one node to the other

takes the delay of dprop ∈ R+ , which is equal to the propagation time.

    Let us assume that a delta impulse is sent off from the local node at the

time tout . It arrives the remote node after a period of dprop . Due to the discretelocal

MAC processing, the delta impulse is only identified at the next remote clock

impulse, which is:

                                                                                 (2)tout + dprop − δ + δtinremote =local

                                                                        inAssuming a MAC processing duration equal to zero and toutremote = tremote , the

remote node immediately sends back a delta impulse representing the acknowl-

edgement. It arrives at the local node after a period of dprop , but is again only

recognized at the next local clock, which is

tin = toutlocalremote + dprop

Then, the observed round trip time rtt is (4).

rtt = tin − tout = tout + dprop − δ + δ + dprop − toutlocallocallocallocal

    = dprop + δ + dprop − δ

(3)

(4)

Next, we assume that the phase changes from one to the next measurement. The

change is constant and is repeated after each phase period starting at zero again.

In the following, we only consider one phase period and assume that round trip

times are measured at all times. Thus, the number of observations is infinite.

The mean rtt over all phase offsets is calculated as follows.

1

1

rtt =

0

rtt dδ =

0

dprop + δ + dprop − δ dδ = 2 · dprop + 1

(5)

The variance of the quantization error is calculated as followed and is simplified

to a cubic function of the fractional part of the round trip distance. Both the

mean and variance are displayed in Fig. 3.

1

σ2 =

0

rtt − rtt

2

dδ = {2dprop } − {2dprop } =

2

1

4

− {2dprop } −

12

2

(6)

 The rtt function produces a pattern which is repeated every phase period. This

reoccurrence introduces a frequency component to be present in the observations.

If two clocks interfere, their phases are equal every beat period, which is the

reciprocal of the beat frequency. The beat frequency is the difference of both

frequencies of both interfering waves ( 7).Thus, the impact of quantization errors

causes a similar effect as the two interfering waves – namely a beat frequency.

fbeat = |f1 − f2 |

5

(7)

Calculated distance and variance

discrete

distribution as

measured

real continuous

distribution as

assumed

3.0

322µs

323µs

324µs

325µs

0.0

0.5

1.0

1.5

2.0

2.5

mean

variance

0.0

0.2

0.4

0.6

0.8

1.0

continuous interval [323µs,325µs[

Actual distance

Fig. 2. Discrete distribution of noisy delay Fig. 3. Theoretical mean distance and

measurements.variance of distance.

Limits and Verification: The accuracy of location and distance sensing algo-

rithms have fundamental limits (refer to the citation in [1]). For example, the

analytic calculations above do not take into account the clock drift during one

RTT observation. Assuming a frequency stability of ±25 ppm and a length of

a transmission sequence of 60 µs and 320 µs, the maximal error could be up to

0.9 m and 4.8 m respectively.

    Furthermore, one should note that only in vacuum light travels at the speed

of light c. In materials the propagation speed depends on the square root of

the dielectric constant ε. For example, dry ferroconcrete has an ε of about 9

and electromagnetic waves traverse through ferroconcrete 3 times slower than in

vacuum. Most other materials used in buildings have lower dielectric constants.

   Another source of possible errors is due to non-line-of-sight conditions. This

results in an overestimation of the distance between the two nodes [12]. Multi-

path propagation might introduce measurement errors because the dominant

path can vary depending on the current transmission conditions. Multi-path

propagation is only present if reflections are given. Reflections can have large

impact on signal strength but only a low one on propagation delay. Thus, in

the presence of multi-path propagation or reflections, we assume time delay

measurement as being more precise than those based on the RSSI.

    In order to check these hypotheses and identify the real measurement resolu-

tion, we conducted experiments. The first measurement campaign was conducted

to study the impact of slow-user motion on packet loss and delay as described

in [10]. At the same time, we also measured the impact of distance on the round

trip times. One year later, we embarked on a second measurement campaign.

We altered the radio modem technology, the location, the analysis software, and

the staff. The consistence of both results proves the reliability and correctness

of our approach.

6

4

Measurements: First and second campaign

Experimental setup: The measurement was conducted twice: First in a gymna-

sium [10] and later in the in the countryside where one could expect the channel

to be free of disturbing noise coming from other radiating devices. The data

communication took place between the local and the remote node. ICMP ping

packets were transmitted each 20 ms (A) respective 10 ms. The measurements

of RTT were conducted for several distances: First covering the range from 5 to

40 m, later extend to the maximal transmission range of 100 m.

    At each distance, we measured for about 15 minutes respective 4 minutes.

One should note, that in this first campaign, the wireless LAN cards were sit-

uated close to the ground. Also, the directions of the antennas were selected at

random and were not recorded. This is important to know as it explains some

of the results presented later. In the second session the sender was placed on a

plastic table, whereas the receiver was installed on top of a 1.5 m wood-metal

ladder. This was to guarantee that a large percentage of the Fresnel-zone, an

elliptic space around the direct line-of-sight between both nodes is free of any

obstacles harming the transmission. This time, the antennas were directed to-

ward each other.

Equipment: The PCs were running a Suse 6.4 Linux system with a 2.4.17 kernel

(A). D-Link cards featuring an Intersil’s (now Conexant) Prism2 chipset were

employed as a wireless interface. Packets were directly sniffed on the MAC layer

by the measurement tool ‘Snuffle’.

    The second time, we used an access point (Netgear FWAG114) support-

ing 802.11b/g as remote node. The PCs were running under Linux, Suse 9.1,

with a special 2.6 kernel. We used two different WLAN cards containing chip

sets from Atheros and Conexant implementing IEEE 802.11 a,b and g. The

Atheros cards (brand Netgear WAG-511, contained an AR5212 chip) are sup-

ported by the Madwifi device driver. We used the software version downloaded

from the CVS server on the August 30th , 2004. The Conexant cards (brand:

Longshine LCS-8531G containing Prism-GT chipset with an ISL3890 as MAC-

Controller) are controlled by the prism54.org device driver (date 28-06-2004,

firmware 1.0.4.3.arm). During each measurement both the sender and monitor

were equipped with cards of the same brand. To gather the packet traces, we

used tcpdump and libpcap.

Configuration: WLAN networking technologies based on the IEEE 802.11 stan-

dards transmit data packets via air. To avoid potential packet delay effects, in

the first experiments the maximal number of retransmissions (transmission type)

was set to zero. The second measurements were conducted in seven different con-

figurations to study the impact of the WLAN card, CPU clock and modulation

type. We used the default configuration of WLAN cards and access point but

changed the supported standard to 802.11g and set the modulation type to ei-

ther 36 or 54 Mbit/s. The frame length of the data packets are 65 bytes and of

the acknowledgements 14 bytes.

7

Time measurements: All three different WLAN cards recorded the arrival time

of packets at a resolution of 1 µs without any variable latency. The precise point

of time, at which the time stamp is recorded, is not documented. Also, the WLAN

chip sets feature only the recording of time stamps of incoming packets. But we

needed both sending and receiving time stamps. Therefore, we decided to use a

third PC to monitor the packets which the local node sends and receives. The

monitor PC was placed close-by the sender to avoid any additional propagation

delays that could falsify the measurements.

    It will be straight forward to alter software and firmware of WLAN cards to

record transmission time stamps, too. Due to legal constraints, we were not able

to implement these changes by ourselves. We expect that WLAN chipset man-

ufactures will provide firmware updates to support precise time stamps because

they will benefit from customers using WLAN for location-aware services. Until

then, we are required to use the third monitoring node.

Data collection & processing: Snuffle provides the packet traces of all 802.11b

packets received at the monitoring node. We filtered-out only the successful ping

sequences which consist of an ICMP request, an acknowledgement, an ICMP

response and again an acknowledgement. Other packets like erroneous transmis-

sions, beacons, ARQ messages etc. were dropped. Due to hardware limitations

of the WLAN card only a fraction of observations were recorded.

     Only the delays fitting in the interval [323 µs, 324 µs] are considered in further

calculations (Fig. 2). A few delay measurements were observed with the value

of 322 and 325 µs. These and all other delays were considered as measurement

errors. Taken the valid packet sequences, the mean and variance of the remote

delay and local delay were calculated. To check for stationary process properties,

the autocorrelation function was calculated.

     In the second round, Tcpdump recorded the packet traces and wrote them

to files. After the measurements we used tcpdump to convert these files to plain

text files. Tcpdump had to be modified in order to print out the prism link-layer

headers. For statistical analysis the R project software turned out to be quite

efficient. Thus, this time we applied R programs to calculate the data’s analyzed

mean, variance and autocorrelation.

Results: The distance was directly derived from the measured propagation delay

using equation (1). Assuming a Gaussian error distribution, we also plotted the

confidence intervals in Fig. 4. In the first campaign the calculated distances were

always higher than the real distances. Also, in some measurements (e.g. 35 m)

the air propagation time was significantly higher. Due to the experimental setup,

we could not ensure that the direct line-of-sight path was taken. The remote node

was placed directly on the ground. Thus, the Fresnel zone was violated and the

direct transmission path was hampered.

    In Fig. 5 the signal strength is displayed as a function of the distance. Theo-

retically, the signal strength should decrease with distance. In this measurement

campaign other factors, such as reflection, seem to be dominant. If one compares

Fig. 4 and Fig. 5, it seems time measurements reflect the distance more precisely

8

Calculated distance [m]

 20 30 40 50 60 70

Received Signal Strength Indicator

Upper bound (95%)

Calculated distance

Actual Distance

Lower bound (5%)I

200

175

ICMP request

150

ACK req.

ICMP responce

ACK resp.

125

y = 104.32e-0.0019x

   R2 = 0.0862

y = 106.33e-0.0024x

   R2 = 0.1397

100

10

75

5

10

15

20

25

30

35

40

5

10

15 20 25 30

Actual Distance[m]

35

40

Distance [m]

Fig. 4. Distance as calculated from RTT Fig. 5. Received signal strength indica-

versus actual distance between both nodes. tion versus distance. Confidence inter-

95% confidence levels are given.vals are too small to be shown.

than RSSI but they have a higher variance and a larger confidence interval. The

results of the second round are illustrated in Fig. 6, which shows the remote

(blue) and local delay (red) measurements, the number of overall observations

(#) and the correlation coefficient (R) for the given configuration. A clear cor-

relation between actual distance and calculated distance can be identified. In

the right graph, one can see that the larger the distance (and the worse the link

quality), the larger the confidence interval becomes. In Fig. 9 we display the

variance of rtt observations over the distance. The curve is highly similar to the

curve described with (6). Thus, our beat-frequency explanation seems to be valid.

Analysis:In [1] we

show that the first mea-

surements follow a weak

stationary process, with

a constant mean, vari-

ance and covariance (for

a constant lag). Thus,

further statistical meth-

ods are applicable: Con-

fidence intervals are only

meaningful if the obser-

vations are independent.

This assumption can be

verified by the autocor-

relation function. The

time-lag dependent au-

tocorrelation coefficients

are presented as a graph

Fig. 6. Propagation delay (=calculated distance)

vs. actual distance (plus 95% conf. intervals).

(blue/upper lines=biased remote delay, red/lower

lines=biased local delays). Each value is based on at

least 1000 observations.

9

Fig. 7. Autocorrelation (=cross correla-

tion of itself) is oscillating for remote de-

lays – indicating a fundamental frequency

component in observations (at 40 m).

Fig. 8. The Fourier transformation of the

observations shows a dominant frequency

at 3.5 Hz, which is only present in the re-

mote delays. (at 40 m).

in Fig. 7. The 40 m results are shown as an example. The autocorrelation for

the local delay is low. It is smaller than ρ=0.05. Thus, the local delay measure-

ments can be seen as independent. The autocorrelation of remote delay values

has the shape of a decaying cosines wave. This kind of autocorrelation curve is

found if the observations feature a constant frequency component. Indeed, this

pattern arises in the delay traces. The values of 323 and 324 occur block-wise in

bursts. We also calculated an FFT over the packet delays. Assuming that each

observation follows the previous after 20 ms, we identified a dominant frequency

of about 3.5 Hz independent of the distance (Fig. 8). However, the lower the

packet error rate, the stronger this effect is. We also calculated the autocorrela-

tion of the second measurement’s second results, high and alternating correlation

coefficients were only present, if we used the Prism GT chip sets. We assume

that this observation is due to the clocking of the MAC protocol and due to the

frequency stability and accuracy of the WLAN quartz crystals. Further studies

are required to understand this effect in-depth. We explain the effect displayed

in Fig. 7 with interference of both remote and local crystal clocks. Taken this

explanation of quantization errors we can calculate the clock drift between both

signals. Assuming a clocking of the MAC protocol at 1 MHz, the drift between

                                                    3.5Hzboth clocks is approximately drif t = fbeat = 1MHz = 3.5ppm. Usually, thef1

tolerance of consumer grade quartz clocks is up to 25 ppm. Thus, we consider

this explanation to be plausible.

     Interestingly, the MAC processing is conducted in steps of 1 µs. Thus, the

MAC processing time is not precisely the SIFS interval but is rounded up to the

next 1 µs. However, the error is small so that receivers tolerate it.

     In our quantization error analysis we calculated the variance which is up to

1/4. A distance of one and a time unit of one in the analysis refer to 300 m or 1 µs

in the experiments. Then, the standard deviation would be 18.75 m or 62.5 ns at

most. The measured standard deviation ranges between 3.3 and 25 m. Thus, the

10

Fig. 9. The variance of rtt Fig. 10. The accuracy (cross correlation and standard

observations over time.error) over the number of observations per position.

quantization error is not the only dominant effect and others such as thermal

noise are important too.

    We measured at each distance for 4 to 15 minutes. Is it really required to

measure that long? In Fig. 10 we consider only a subset of all rtt observations

taken during the second campaign. We display the correlation coefficient R and

the standard error over the number of observations per distance. With 500 to

1000 observations per position nearly the optimal accuracy is achieved. If one

assumes that a packet is sent off every mircosecond, the distance can be estimated

after 1 s of continues transmission.

5

Conclusion

We have presented an algorithm to measure the air propagation time of IEEE

802.11 packets with a higher accuracy. Using two different experimental setups,

we determined the precision of round trip time measurements. We used com-

mercial WLAN cards, supporting IEEE 802.11b and 802.11g, implemented with

three different WIFI chip sets. We have shown that such time measurements

are possible even with off-the-shelf, commercial WLAN equipment and without

additional signal processing hardware.

   To overcome the low resolution of the clocks, numerous observations have to

be combined and smoothened. This can be carried out best during an ongoing

data transmission at no additional cost. We explained why smoothing indeed

helps to enhance the resolution of the time difference measurement so that dis-

tance measurements become possible. This effect can be due to the presence of

measurement noise and to the beat frequency resulting from drifting clocks. To

the best of our knowledge, especially the latter explanation is novel.

   Our finding suggests that instead of RSSI the round trip time should be mea-

sured because it is correlated with the distance more strongly. In our gymnasium

measurement the RSSI has not been useful to identify the distance because –

due to reflections – the attenuation varied largely.

11

    The contribution of this work is to show that neither synchronized, precise

clocks nor special hardware is required if the propagation delay between two

WLAN nodes is to be measured. This allows the implementation of easy-to-

use, cheap and precise indoor positioning systems, which do not require maps

containing signal strength distributions. However, WLAN chipset manufacturers

should update their firmware so that it reports the round trip time of packets

with an accuracy of at least 1 µs. Then, a 1000 packets transmission – achievable

in less than one second – can measure the distance with an error deviation of

less than 8 m.

Acknowledgements

We like to thank Prof. Wolisz for his ongoing support, E.-L. Hoene for the

revision, and Sven Lamprecht and David Hundenborn for conducting the second

measurements.

References

 1. G¨nther, A., Hoene, C.: Measuring round trip times to determine the distance be-u

    tween WLAN nodes. Technical Report TKN-04-016, Telecommunication Networks

    Group, Technische Universit¨t Berlin (2004)a

 2. Hightower, J., Borriello, G.: Location systems for ubiquitous computing. IEEE

    Computer 34 (2001) 57–66

 3. He, T., Huang, C., Blum, B.M., Stankovic, J.A., Abdelzaher, T.: Range-free lo-

    calization schemes for large scale sensor networks. In: Proceedings of MOBICOM,

    San Diego, CA, ACM Press (2003) 81–95

 4. Bahl, P., Padmanabhan, V.N.: RADAR: An In-Building RF-Based User Location

    and Tracking System. In: Infocom 2000, Tel-Aviv, Israel (2000) 775–784

 5. Velayos, H., Karlsson, G.: Limitations in range estimation for wireless LAN. In:

    Proc. 1st Workshop on Positioning, Navigation and Communication (WPNC’04),

    Hannover, Germany (2004)

 6. Alsindi, N., Li, X., Pahlavan, K.: Performance of TOA estimation algorithms in

    different indoor multipath conditions. In: IEEE Wireless Communications and

    Networking Conference (WCNC). Volume 1. (2004) 495–500

 7. Enge, P., Misra, P., eds.: Special issue on GPS: The Global Positioning System,

    IEEE (1999)

 8. Werb, J., Lanzl, C.: Designing a positioning system for finding things and people

    indoors. IEEE Spectrum 35 (1998) 71–78

 9. Lepak, J., Crescimanno, M.: Speed of light measurement using ping. American

    Physical Society - Meeting Abstracts (2002) abstract B2.009.

10. Hoene, C., G¨nther, A., Wolisz, A.: Measuring the impact of slow user motion onu

    packet loss and delay over IEEE 802.11b wireless links. In: Proc. of Workshop on

    Wireless Local Networks (WLN) 2003, Bonn, Germany (2003)

11. Gammaitoni, L., Hanggi, P., Jung, P., Marchesoni, F.: Stochastic resonance. Re-

    views of Modern Physics 70 (1998) 223–287

12. Cong, L., Zhuang, W.: Non-line-of-sight error mitigation in mobile location. In:

    Infocom 2004, Hong Kong (2004) 650– 659

12