研发类校园招聘
百度2014研发类校园招聘笔试题解答
一、简答题
1. 在现代系统的设计过程中,为了减轻请求的压力,通常采用缓存技术,为了进一步提升缓存的命中率,同常采用分布是缓存方案。调度模块针对不同内容的用户请求分配给不同的缓存服务器向用户提供服务。请给出一个分布式缓存方案,满足如下要求:
1) 单台缓存服务器故障,整个分布式缓存集群,可以继续提供服务。
2)通过一定得分配策略,可以保证充分利用每个缓存服务的存储空间,及负载均衡。当部分服务器故障或系统扩容时,改分配策略可以保证较小的缓存文件重分配开销。
3)当不同缓存服务器的存储空间存在差异时,分配策略可以满足比例分配。
一、简答题
a. 共享:多个应用程序可以使用同一个动态库,启动多个应用程序的时候,只需要将动态库加载到内存一次即可;
b. 开发模块好:要求设计者对功能划分的比较好。
缺点是不能解决引用计数等问题。
(2)静态库(Static Library):函数和数据被编译进一个二进制文件(通常扩展名为.LIB)。在使用静态库的情况下,在编译链接可执行文件时,链接器从库中复制这些函数和数据并把它们和应用程序的其它模块组合起来创建最终的可执行文件(.EXE文件)。静态链接库作为代码的一部分,在编译时被链接。优缺点如下:
代码的装载速度快,执行速度也比较快,因为编译时它只会把你需要的那部分链接进去,应用程序相对比较大。但是如果多个应用程序使用的话,会被装载多次,浪费内存。
1)共享锁
SQL Server中,共享锁用于所有的只读数据操作。共享锁是非独占的,允许多个并发事务读取其锁定的资源。默认情况下,数据被读取后,SQL Server立即释放共享锁。例如,执行查询“SELECT * FROM my_table”时,首先锁定第一页,读取之后,释放对第一页的锁定,然后锁定第二页。这样,就允许在读操作过程中,修改未被锁定的第一页。但是,事务 隔离级别连接选项设置和SELECT语句中的锁定设置都可以改变SQL Server的这种默认设置。例如,“ SELECT * FROM my_table HOLDLOCK”就要求在整个查询过程中,保持对表的锁定,直到查询完成才释放锁定。
2)修改锁
修 改锁在修改操作的初始化阶段用来锁定可能要被修改的资源,这样可以避免使用共享锁造成的死锁现象。因为使用共享锁时,修改数据的操作分为两步,首先获得一 个共享锁,读取数据,然后将共享锁升级为独占锁,然后再执行修改操作。这样如果同时有两个或多个事务同时对一个事务申请了共享锁,在修改数据的时候,这些 事务都要将共享锁升级为独占锁。这时,这些事务都不会释放共享锁而是一直等待对方释放,这样就造成了死锁。如果一个数据在修改前直接申请修改锁,在数据 改的时候再升级为独占锁,就可以避免死锁。修改锁与共享锁是兼容的,也就是说一个资源用共享锁锁定后,允许再用修改锁锁定。
3)独占锁
独占锁是为修改数据而保留的。它所锁定的资源,其他事务不能读取也不能修改。独占锁不能和其他锁兼容。
4)结构锁
结构锁分为结构修改锁(Sch-M)和结构稳定锁(Sch-S)。执行表定义语言操作时,SQL Server采用Sch-M锁,编译查询时,SQL Server采用Sch-S锁。
5)意向锁
意 向锁说明SQL Server有在资源的低层获得共享锁或独占锁的意向。例如,表级的共享意向锁说明事务意图将独占锁释放到表中的页或者行。意向锁又可以分为共享意向锁、 独占意向锁和共享式独占意向锁。共享意向锁说明事务意图在共享意向锁所锁定的低层资源上放置共享锁来读取数据。独占意向锁说明事务意图在共享意向锁所锁定 的低层资源上放置独占锁来修改数据。共享式独占锁说明事务允许其他事务使用共享锁来读取顶层资源,并意图在该资源低层上放置独占锁。
6)批量修改锁
批量复制数据时使用批量修改锁。可以通过表的TabLock提示或者使用系统存储过程sp_tableoption的“table lock on bulk load”选项设定批量修改锁。
二、算法设计题
// 求比指定数大且最小的“不重复数” #include <stdio.h> void minNotRep(int n) { // 需要多次判断 while(1) { int a[20], len = 0, i, b = 0; // flag为true表示是“重复数”,为false表示表示是“不重复数” bool flag = false; // 将n的各位上数字存到数组a中 while(n) { a[len++] = n % 10; n = n / 10; } // 从高位开始遍历是否有重复位 for(i = len - 1; i > 0; i--) { // 有重复位则次高位加1(最高位有可能进位但这里不需要额外处理) if(a[i] == a[i - 1] && !flag) { a[i - 1]++; flag = true; } else if(flag) { // 将重复位后面的位置为0101...形式 a[i - 1] = b; b = (b == 0) ? 1 : 0; } } // 重组各位数字为n,如果是“不重复数”则输出退出否则继续判断 for(i = len - 1; i >= 0; i--) { n = n * 10 + a[i]; } if(!flag) { printf("%d\n", n); break; } } } int main() { int N; while(scanf("%d", &N)) { minNotRep(N + 1); } return 0; }
-
当i==j时,P[i][j]=true
-
当i+1==j时,P[i][j]=str[i]==str[j]
-
其他,P[i][j]=P[i+1][j-1]&&(str[i]==str[j])
那么P[i][j]中j-i+1最大的且值为true的就是最长回文子串。这样,这个方法的时间复杂度为O(n^2),空间复杂度为O(n^2)。比暴力法有很大的改进。
Source Code:
#include <stdio.h> #include <stdlib.h> #include <string.h> int longestPalSubstr(char *str) { int n = strlen(str); int i, j, len, maxlen = 0, maxi = 0, maxj = 0; bool **P = (bool**)malloc(sizeof(bool) * n); for(i = 0; i < n; i++) { P[i] = (bool*)malloc(sizeof(bool) * n); } // initialize P[i][i] for(i = 0; i < n; i++) { P[i][i] = true; } // compute P[n][n] by length for(len = 2; len <= n; len++) { for(i = 0; i < n - len + 1; i++) { j = i + len - 1; if(len == 2) { P[i][j] = (str[i] == str[j]); } else { P[i][j] = ((str[i] == str[j]) && P[i + 1][j - 1]); } } } // int k; for(i = 0; i < n; i++) { for(j = i; j < n; j++) { // printf("%d ", P[i][j]); if(P[i][j] && maxlen < (j - i + 1)) { maxlen = j - i + 1; maxi = i; maxj = j; } } // printf("\n"); // for(k = 0; k <= i; k++) // printf(" "); } printf("The longest palin substr is "); for(i = maxi; i <= maxj; i++) { printf("%c", str[i]); } printf(", maxlen is %d\n\n", maxlen); return maxlen; } int main() { char str[100]; while(1) { gets(str); if(strlen(str) == 0) break; longestPalSubstr(str); } return 0; }
算法3:第三个方法,可以从上面那个方法的状态转移方程获得启发,对于每一个回文子串可以先确定一个中心,然后向两边扩展,这样可以在时间复杂度O(n^2),空间复杂度O(1)的情况下完成,需要注意的是,长度为奇数和偶数的中心的情况是不同的。
Source Code:
#include <stdio.h> #include <stdlib.h> #include <string.h> int longestPalSubstr(char *str) { int len = strlen(str); int i, maxLen = 1, start = 0; int low, high; // 将每个字符作为中心向两边扩展判断 for(i = 1; i < len; i++) { // 处理长度为偶数的情况 low = i - 1; high = i; while(low >= 0 && high < len && str[low] == str[high]) { if(maxLen < high - low + 1) { start = low; maxLen = high - low + 1; } low--; high++; } // 处理长度为奇数的情况 low = i - 1; high = i + 1; while(low >= 0 && high < len && str[low] == str[high]) { if(maxLen < high - low + 1) { start = low; maxLen = high - low + 1; } low--; high++; } } printf("The longest palin substr is "); for(i = start; i < start + maxLen; i++) { printf("%c", str[i]); } printf(", maxlen is %d\n\n", maxLen); return maxLen; } int main() { char str[100]; while(1) { gets(str); if(strlen(str) == 0) break; longestPalSubstr(str); } return 0; }
算法4:第四个方法采用后缀数组,将最长回文子串的问题转化为最长公共前缀的问题。具体的做法就是:将整个字符串翻转之后,拼接到原字符串后,注意用特殊字 符分开,这样问题就变成了新的字符串的某两个后缀的最长公共前缀的问题了。这个方法比较强大,很多字符串的问题都能够巧妙的解决。不过实现起来也相对比较:难,好的实现和差的实现时间复杂度相差很大。由于对后缀数组不是很清楚,未写代码,等学习了后缀数组再过来补。
算法5:第五个方法叫做Manacher算法,是一种线性时间的方法,非常巧妙。首先,我们在上面的方法中个,都要考虑回文长度为奇数或者偶数的情况。这个:方法,引入一个技巧,使得奇数和偶数的情况统一处理了。具体做法如下:
abba转换为#a#b#b#a#,也就是在每一个字符两边都加上一个特殊字符。
然后创建一个新的P[i]表示,以第i个字符为中心的回文字串的半径。例如上面的例子,对应的P如下,设S为原始字符串:
| S | # | a | # | b | # | b | # | a | # |
| P | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 |
通过观察上面的表,大家可以发现P[i]-1就是实际回文字串的长度。如果知道P,遍历一次就知道最长的回文子串。可以该如何计算P呢?这是这个算法最核心的部分。
下面的讨论基本转自博客:http://www.felix021.com/blog/read.php?2040 该博客中对Manacher算法介绍得也非常好,向大家推荐。
算法引入两个变量id和mx,id表示最长回文子串的中心位置,mx表示最长回文字串的边界位置,即:mx=id+P[id]。
在这里有一个非常有用而且神奇的结论:如果mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i) 分开理解就是:
-
如果mx - i > P[j], 则P[i]=P[j]
-
否则,P[i] = mx - i.
这两个该如何理解呢?具体的解释请看下面的两个图。
(1)当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
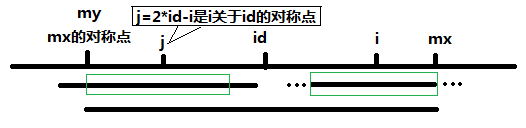
(2)当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是 说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。
对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
理解了上面的一点,就没有问题了。
Source Code:
#include <stdio.h> #include <stdlib.h> #include <string.h> int longestPalSubstr(char *str) { char s[100]; int i, maxLen = 1, start = 0, j; int len = strlen(str); int mx = 0, id = 0, min; s[0] = '$'; s[1] = '#'; for(i = 0, j = 2; i < len; i++, j += 2) { s[j] = str[i]; s[j + 1] = '#'; } s[j] = '\0'; len = len * 2 + 1; int *p = (int *)malloc(sizeof(int) * len); memset(p, 0, len); p[0] = 1; for(i = 1; i < len; i++) { min = p[2 * id - i] > (mx - i) ? (mx - i) : p[2 * id - i]; p[i] = mx > i ? min : 1; while(s[i + p[i]] == s[i - p[i]]) { p[i]++; } if(i + p[i] > mx) { mx = i + p[i]; id = i; } } for(i = 0; i < len; i++) { //printf("%d ", p[i]); if(maxLen < p[i] - 1) { maxLen = p[i] - 1; start = i - maxLen; } } printf("The longest palin substr is "); for(i = start; i < start + 2 * maxLen + 1; i++) { if(s[i] != '#') { printf("%c", s[i]); } } printf(", maxlen is %d\n\n", maxLen); return maxLen; } int main() { char str[100]; while(1) { gets(str); if(strlen(str) == 0) break; longestPalSubstr(str); } return 0; }
// 求最大覆盖点 #include <stdio.h> int maxCover(int a[], int n, int L) { int count = 2, maxCount = 1, start; int i = 0, j = 1; while(i < n && j < n) { while(a[j] - a[i] <= L && j < n) { j++; count++; } if(a[j] - a[i] <= L) { if(maxCount < count) { start = i; maxCount = count; } i++; j++; } else { i++; count--; } } printf("covered point: "); for(i = start; i < start + maxCount; i++) { printf("%d ", a[i]); } printf("\n"); return maxCount; } int main() { // test int a[] = {1, 3, 7, 8, 10, 11, 12, 13, 15, 16, 17, 18, 21}; printf("max count: %d\n", maxCover(a, 11, 8)); return 0; }