Voronoi Diagram——维诺图
Voronoi图定义
任意两点p 和q 之间的欧氏距离，记作 dist(p, q) 。就平面情况而言，我们有
dist(p, q) = (px-qx)2+ (py-qy)2
设P := {p1, …, pn}为平面上任意 n 个互异的点；这些点也就是基点。按照我们的定义，所谓P对应的Voronoi图，就是平面的一个子区域划分——整个平面因此被划分为n 个单元（cell ），它们具有这样的性质：
任一点q位于点pi 所对应的单元中，当且仅当对于任何的pj∈Pj, j≠i,
都有dist(q, pi)<dist(q, pj)。我们将与P对应的Voronoi图
记作Vor(P)。
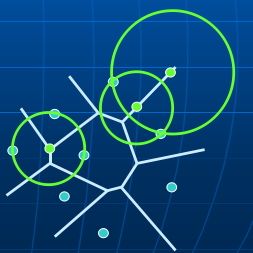
“Vor(P) ”或者“Voronoi图”所指示的仅仅只是组成该子区域划分的边和顶点。在Vor(P)中，与基点pi 相对应的单元记作V (pi)——称作与pi 相对应的Voronoi单元（Voronoi cell）。上图是Voronoi图，下图的蓝色点围成的区域（凸包）是它对应的Delaunay三角剖分。
任给平面上两点p 和q ，所谓 p 和q 的平分线（bisector），就是线段 pq的垂直平分线。该平分线将平面划分为两张半平面（half-plane）。点 p 所在的那张开半平面记作 h(p, q) ，点 q 所在的那张开半平面记作 h(q, p) 。请注意，r ∈ h(p, q) 当且仅当 dist(r, p) < dist(r, q) 。据此，可以得出如下观察结论：
V (pi) = ∩ h(pi, pj) , 1≤j≤n, j≠ i
也就是说，V (pi)是(n-1)张半平面的公共交集；它也是一个（不见得有界的）开的凸多边形（convex polygon）子区域.
很显然，Voronoi顶点到相邻的三个site距离相等；Voronoi边上任意一点到相邻的两个site距离相等；
对于任何点q，我们将以q为中心、内部不含P中任何基点的最大圆，称作q关于P的最大空圆（largest empty circle ），记作Cp(q)。以下定理指出了Voronoi图的顶点及边所具有的特征：
对于任一点集P 所对应的Voronoi图Vor(P) ，下列命题成立：
1) 点q 是Vor(P) 的一个顶点，当且仅当在其最大空圆Cp(q)的边界上，至少有三个基点； (Voronoi顶点是三个site的外接圆的圆心)
2) pi 和pj 之间的平分线确定了Vor (P) 的一条边，当且仅当在这条线上存在一个点 q，Cp(q)的边界经过pi 和pj，但不经过其它站点。
构造Voronoi图
构造Voronoi图有四种算法：定义法（Intersect of Halfplanes）、增量（incremental）算法、分治法、plane sweep算法；
1、plane sweep（平面扫描）算法又名Fortune算法，它主要由两部分组成：sweep line（扫描线）和beach line（海滩线）；
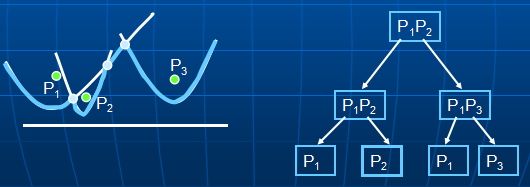
Fortune算法建立在点、线之间的距离关系上，如下图所示，平面上任意一点到一个点p的距离与到一条直线l的距离相等，这样的点有很多，它们构成的轨迹就是抛物线，点p就是抛物线的焦点，直线l就是抛物线的准线；
2、回到Fortune算法，这个固定点p就是一个site，l就是sweep line；
sweep line自上而下扫描，平面区域任何点到site与sweep line距离相等的点构成一条抛物线（site就是抛物线的焦点），则n个site的抛物线相交的若干段抛物线弧构成beach line，如下图的蓝色抛物线弧集合；
抛物线之间的交点称为断点（break point），每个断点都落在某条Voronoi 边上。这并非巧合，随着扫描线自上而下扫过整个平面，所有断点的轨迹合起来恰好就是待构造的Voronoi图；（几何证明：断点到相邻的两个site距离总是相等，这个关系随着sweep line的扫描一直不变，则断点的运动轨迹就是这两个site的垂直平分线，也即Voronoi 边，两条Voronoi 边相交又产生Voronoi 顶点）
beach line上方的Voronoi 顶点和Voronoi 边已确定，将不会再变化。beach line（曲线）和它上方的直线构成当前的Voronoi 边，最后随着sweep line的移动而beach line也在不断下移，变为最终的Voronoi 边； （海滩线沿x 方向单调——即，它与任一垂线相交而且仅相交于一点。）
beach line属性
1、随着sweep line下降，break points跟踪Voronoi边；一个新的break point（新弧形成或者两个break point融合为一体）产生一条新的边；
2、两个break point相遇产生voronoi顶点
3、为了确定Voronoi 边和Voronoi 顶点，我们需要维护beach line这个结构，但是随着l 的运动它会持续不断地更新。那么，应该如何表示beach line结构呢？
所谓beach line的组合结构发生变化，指的是其上出现了新的抛物线弧，或原有的某段抛物线弧收缩成一个点并进而消失。在这个算法中，产生新弧，称为site event；旧弧消失，称为circle event。
两类事件site event和circle event：
1）、site event
sweep line扫到某个site，设为p，在此瞬间，站点p对应于一条宽度为零的退化抛物线——亦即，将该新站点p与扫描线l联接起来的垂直线段。随着扫描线继续下移，这个宽度为0的抛物线将逐渐伸展开来。
site event发生后引起的变化：因为沿海滩线上各个断点的运动轨迹，就勾勒出了Voronoi 图的各边。所以每发生一次site事件，就会生成两个新的断点，此后它们会逐渐地勾勒出同一条新边。
那为什么是同一条新边呢？实际上，在刚刚诞生的那一瞬间，这两个断点相互重合，然后才会各自朝相反的方向运动，而且它们所勾勒的都是同一条边（同break point定义处的几何证明）。在一开始，这条边与Voronoi图位于扫描线之上的其它部分并不相联。随着这条边的不断生长，直到后来它们与其它边相遇，此时它才会与Voronoi图的其它部分联接起来。
定理：只有在发生某个site事件时，海滩线上才会有新的弧出现。
2）、circle event
发生于原有的某段弧收缩为一点并即将消失时，假设三段连续的弧α 、α '和α ''，这三段弧必然分别对应于三个不同基点pi 、pj和pk ，就在α'即将消失的那一刻，这三个基点所对应的抛物线将相交于同一点q 。此时点q 到扫描线l 与到这三个基点等距离。亦即，存在一个以q 为中心、穿过pi、pj和pk 的圆，且该圆在最低点处与l 相切。该圆的内部不可能有任何基点——否则，q 到该基点将比到l 更近，而这却与“q 位于海滩线上”的事实不合。因此，点q 必是Voronoi图的一个顶点。
若海滩线上有某段弧消失，并因而有两段弧汇合起来，则相应地在Voronoi图中肯定也会有两条边汇合起来（成为一条新的边）。海滩线上依次首尾相联的任何三段弧，其对应的三个基点都会确定一个外接圆；当扫描线触及某个这类外接圆的最低点时，也就发生了一次圆事件（circle event ）
定理：海滩线上已有的弧，只有在经过某次圆事件之后，才有可能消失。
简单点说，site event发生时，beach line会产生一条新弧，同时就会有一条新边出现并朝两端生长，慢慢形成新的Voronoi边；circle event发生时，会有两条正在生长的Voronoi边汇合起来，并在接合处形成一个Voronoi 顶点，同时中间的旧弧消失。
4、异常情况
a false alarm：We may have stored a circle event in the event list, but it may be that it never happens
There are two reasons for false alarms: site events and other circle events
我们存储了circle event，但它可能永远不会发生，真是一个美丽的错误... 在site event和circle event发生时，都会有可能误报情况。
1）、site event：circle event发生时产生的最大空心圆内部还有其他site。
如下面三个图例，p2、p3、p4组成的外接圆，确定了一个circle event，外接圆y坐标最小的点（图中最低的小红点）将进入PQ，但是在sweep line碰到它之前，先扫描到了site p7，这样一来将产生新弧，破坏了原来的<p2,p3,p4>三元组。发生circle event时，并不知道这是一个false alarm，所以直到碰到该外接圆内部存在site。这时需要把这个circle event去掉，也即删除原先进入PQ中的最低点。也说明了这个外接圆的圆心不是Voronoi顶点，属于误报。
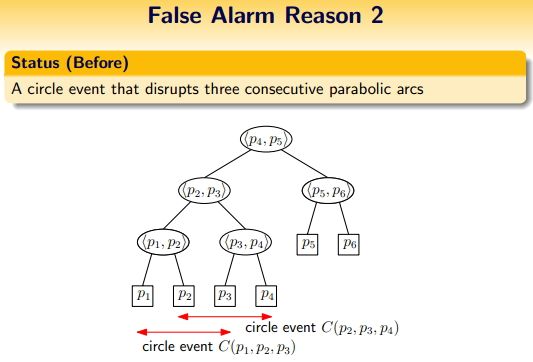
2）、circle event：该事件还没有来得及真正发生，这一邻接弧三元组就已经消失了。
如下面三个图例，<p2,p3,p4>三元组先产生外接圆，第一个小红点进入PQ，当sweep line扫描到p1时，<p1,p2,p3>三元组也产生外接圆，第二个小红点进入PQ；但是，当sweep line扫描到第一个小红点时，它从PQ出队，随着sweep line下移，α3消失，<α2,α3,α4>合并为<α2,α4>破坏了原来的三元组，则<p1,p2,p3>无法形成Voronoi顶点，也即这个circle event属于误报。需要删除PQ中第二个小红点。
图像说明： bayanbox.ir/id/3367913281004602743?download
相关数据结构
构建Voronoi图需要三个数据结构，分别是平衡二叉树AVL，优先队列PQ和双向边链表DCEL。
1、beach line数据结构AVL：记录beach line的状态，包括break points, and the arcs currently on beach line
一个叶子结点表示一段弧，因为每个弧都一 一对应一个site，所以用site number来存储；
非叶子结点则表示两条弧的交点即断点，用两条弧对应的site对存储；因为弧和断点都是不断变化的，所以都用固定的site number来表示。
此例中AVL中的p1、p2表示原图的site p1和site p2对应的弧，<p1,p2>表示两弧的交点即断点，其实AVL树就是site和break point的中序遍历。
若按照这样的方式来表示beach line，每遇到一个新的site，都可以在O(logn)时间内，沿beach line找出位于该site上方的那段弧：在查找过程中，在每个内部节点处，只要将其对应断点的x坐标，与新site的x坐标做一比较。
为了处理false alarm的第二种情况，T 的一片叶子若对应于某段弧α，则为它配备一个指针，指向PQ中的一个（事件）节点——具体说，就是（在将来可能）导致α 消失的那个圆事件所对应的节点。若没有导致α消失的圆事件，或者还没有发现这样一个事件，则该指针被置为nil。
最后，每个内部节点v 也配有一个指针，指向与当前Voronoi 图对应的双向链接边表DCEL中的某条半边（half-edge ）——更确切地说，此时与 v 相对应的断点，正在勾勒出的一条 Voronoi边，而v 的指针就指向这条边所对应的那条半边。
处理：新的site产生一条新弧，对应的旧弧被删除（DS中对应AVL某叶子节点被删除）；同时，该旧弧指向的event也将被删除（DS对应PQ中删除一个元素）；
添加弧操作：replacing the leaf with a sub-tree
删除弧操作：deleting a leaf from the tree
2、事件队列PQ：Event queue（on decreasing y-coordinate）
记录扫描线当前状态的结构。存储已确定即将发生的events。对于site event，在sweep line开始扫描之前就可以全部送入PQ；
对于circle event, 不仅要记录该外接圆的最低点（外接圆与sweep line的切点），还要设置一个指针指向AVL中的某片叶子——这片叶子所对应的，就是在该事件发生时即将随之消失的那段弧。
如果某三个site形成的外接圆，该圆对应的纵坐标最小的点（即未来的切点）在sweep line的下面，则为circle event；并将该点入优先队列；并且这三个连续的sites与该切点互相链接对方。对于false alarm的第一种情况还需处理。
处理：sweep line扫描到切点，三条弧变成两条弧，形成Voronoi顶点；删除三条弧中间的那条，对应DS则为删除叶子节点，并在PQ中删除该节点指向的event（若有，即为一个false alarm），同时将合并后的两条弧分别与原先三条弧的左右两侧各一条弧结合，形成两个新的三元组，将两新三元组对应的两切点加入PQ，并做指针链接；
3、双向边链表（DCEL）：记录Voronoi状态，包含half-edges, edges（一对half-edge）, vertices and cell records（A chain of counter-clockwise half-edges）
At the leaves of the tree, a pointer to the circle event is stored, if the arc defines a circle event. If not, pointer is set to NULL. By maintaining this pointer, we do not have to perform any search after encountering false events.
算法伪码
算法 VORONOID IAGRAM (P)
输入：平面点集 P := {p1, …, pn)
输出：以双向链接边表 D 表示的（限制在一个足够大的包围框之内的）Voronoi 图Vor(P)
1.初始化事件队列Q ：将所有的基点事件插入其中
初始化状态结构T ：将其置空
初始化双向链接边表D ：将其置空
2. while ( Q 非空)
3. do 将y- 坐标最大的事件从 Q 中取出
4. if ( 这是一个发生于基点 pi 处的基点事件)
5. then HANDLESITE EVENT(pi)
6. else HANDLECIRCLE EVENT(γ)
(* 这里的γ是T 的一匹叶子，它对应于那段即将消失的弧 *)
7.(* 仍然存在于 T 中的那些内部节点，对应于 Voronoi 图的单向无穷边 *)
计算出一个包围框，其尺寸之大，应足以容下Voronoi 图中的所有顶点
通过对双向链接边表的适当调整，将这些单向无穷边都联接到这个包围框上
8.遍历双向链接边表中的所有半边增加相应的单元记录
设置好指向这些单元的指针，以及由这些单元发出的（指向对应各边的）指针
输入：平面点集 P := {p1, …, pn)
输出：以双向链接边表 D 表示的（限制在一个足够大的包围框之内的）Voronoi 图Vor(P)
1.初始化事件队列Q ：将所有的基点事件插入其中
初始化状态结构T ：将其置空
初始化双向链接边表D ：将其置空
2. while ( Q 非空)
3. do 将y- 坐标最大的事件从 Q 中取出
4. if ( 这是一个发生于基点 pi 处的基点事件)
5. then HANDLESITE EVENT(pi)
6. else HANDLECIRCLE EVENT(γ)
(* 这里的γ是T 的一匹叶子，它对应于那段即将消失的弧 *)
7.(* 仍然存在于 T 中的那些内部节点，对应于 Voronoi 图的单向无穷边 *)
计算出一个包围框，其尺寸之大，应足以容下Voronoi 图中的所有顶点
通过对双向链接边表的适当调整，将这些单向无穷边都联接到这个包围框上
8.遍历双向链接边表中的所有半边增加相应的单元记录
设置好指向这些单元的指针，以及由这些单元发出的（指向对应各边的）指针
处理两类事件的子程序分别如下：
算法 HANDLESITE EVENT(pi)
算法 HANDLESITE EVENT(pi)
算法 HANDLECIRCLE EVENT(γ)
1.将（对应于即将消失的弧α的那匹）叶子γ，从T 删除掉
检查相关的内部节点，更新其中表示有关断点的基点对信息
若有必要，须对T 做调整，以使之重新平衡
在Q 中，删除所有与α相关的圆事件
(* 在T 中，γ的前驱与后继节点配有相应的指针 *)
(* 借助这些指针，就可以找出这些事件 *)
（α在其中居中的那个圆事件，此刻正在接受处理，并已经从Q 被删除掉了）
2. 更新存储当前Voronoi图的双向链接边表D ：
对应于该事件的圆心生成一个Voronoi顶点记录，并将该记录插入双向链接边表；
对应于海滩线上新生出的断点,并生成两个半边记录，正确地设置好它们相互之间的指针；
将这三个新记录，与同样终止于该Voronoi顶点的其它半边链接起来
3. (* 此前与α紧邻于左侧的那段弧，现可能在某个新的邻接弧三元组中居中 *)
检查该邻接弧三元组所对应的两个断点是否汇合为一点
果真如此，则
将对应的圆事件插入到事件队列Q 中，并
在Q 中该节点和 T 中与之对应的节点之间设置指针，使它们相互指向对方
(* 此前与α紧邻于右侧的那段弧，现也可能在某个新的邻接弧三元组中居中 *)
对该弧，做类似的处理。
算法复杂度
给定由平面上任意n 个基点构成的一个集合，其对应的 Voronoi图可以采用扫描线算法，在 O(nlogn)时间内、使用O(n)空间构造出来。因为Voronoi图可以归约为n个实数的排序问题，则最好时间复杂度为O(nlogn)，即sweep line算法是最优的。
定义法：O(n^2logn)，增量算法：O(n^2)，分治法：O(nlogn)，sweep line算法：O(nlogn)。
参考
sweep line作者主页：http://ect.bell-labs.com/who/sjf/