实现Avl平衡树
实现Avl平衡树
一、介绍
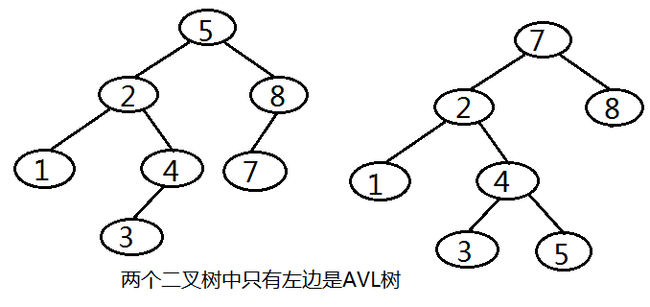
AVL树是一种自平衡的二叉搜索树,它由Adelson-Velskii和 Landis于1962年发表在论文《An algorithm for the organization of information》中。AVL树的特点是,其左右子树的高度差的绝对值小于2(空树的高度定义为 -1,无子树的树高度为0)。如下图所示,左边的二叉树为AVL树,而右边的二叉树root节点的左子树高度为2,右子树高度为0,高度差为2,不是AVL树。与普通二叉树相同的是查找和遍历;但是插入和删除操作可能会破坏AVL的平衡结构,这也是实现AVL树的难点所在。
二、定义
AVL的特点是平衡,每个节点平衡依赖于其左右子树的高度,因此,每个树节点都有一个height值。这里的定义和实现来自于《数据结构和算法分析-C语言描述》一书,具体定义如下:
/* filename: Avltree.h from: chapter 4 tree, page 87, Data Structure and Algorithm Analysis date: 2013-08-06 function: declearation of AVL Tree */ #ifndef _AVLTREE_H_ #define _AVLTREE_H_ // 定义树节点 struct AvlNode{ double element; //内容元素 AvlTree left; //左孩子 AvlTree right; //右孩子 int height; //高度,无子节点时为 0,NULL时为 -1 }; typedef struct AvlNode * Position; typedef struct AvlNode * AvlTree; void InitAvl(AvlTree *T); AvlTree MakeEmpty(AvlTree T); Position Find(double X, AvlTree T); Position FindMin(AvlTree T); Position FindMax(AvlTree T); AvlTree Insert(double X, AvlTree T); AvlTree Delete(double X, AvlTree T); double Retrieve(Position P); #endif
对节点高度的控制是通过Height(Position P)实现的,很重要的一点是它规定了空树的高度(此时调用P->height会报错)。Height(Position P)实现如下:
static int Height(Position P){ if(P==NULL) return -1; else return P->height; }
三、初始化和置空树
创建一个新树时,使用InitAvl()函数将其初始化为空。删除所有节点使用MakeEmpty()函数,代码如下:
/* filename: Avltree.c */ void InitAvl(AvlTree *T){ *T = NULL; } AvlTree MakeEmpty(AvlTree T){ if(T!=NULL){ MakeEmpty(T->left); MakeEmpty(T->right); free(T); } return NULL; }
四、实现查找
AVL树的查找与普通二叉树没有区别,可以通过递归或者非递归的方式实现,都比较简单。这里使用的是递归,需要注意,Find()、FindMin()和FindMax()方法前的return 比不可少,否则递归得出的结果无法向上传递。
Position Find(double X, AvlTree T){ if(T!=NULL){ if(X==T->element) return T; else if(X>T->element) return Find(X, T->right); else return Find(X, T->left); }else return T; } Position FindMin(AvlTree T){ if(T!=NULL && T->left!=NULL) return FindMin(T->left); else return T; } Position FindMax(AvlTree T){ if(T==NULL ||T->right==NULL) return T; else return FindMin(T->right); }
五、实现插入
在插入之前,AVL树中每个节点都是平衡的,插入元素以后,可能会导致 插入节点到根节点路径上的节点的平衡发生改变,而插入节点的子节点的平衡不变。沿着这条路径上行,对路径上的每个节点,检查其平衡状态,修正不平衡的节点,修正height,一直检查和修正到root节点。最后可以得到的是一棵平衡的AVL树。
假设我们遍历到的节点是a,如果a满足平衡条件,则上行一个节点。如果不满足,则有四种情况:
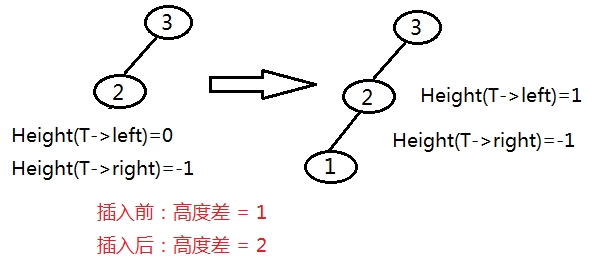
- 插入到a的左儿子的左子树后,平衡被打破,(结果:左高右低,left-left型)(例子见上图)
- 插入到a的左儿子的右子树后,平衡被打破,(结果:左高右低,left-right型)
- 插入到a的右儿子的左子树后,平衡被打破,(结果:右高左低,right-left型)
- 插入到a的右儿子的右子树后,平衡被打破,(结果:右高左低,right-right型)
情形1和情形4对称,情形2和情形3对称。这里先看情形1。需要通过旋转来调整这几种不平衡状态
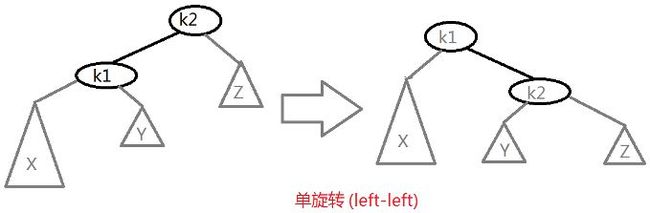
1、Left-left case
这里,K2是当前要处理的节点。可以看到K2->left 比 K2->right 要高两层,而X比Y要高一层。而插入之前,k2满足平衡条件。插入新元素导致 X 长出一层,使其比Z高两层。重新调整平衡的方法是使X上移一层,Z下移一层,同时将K1设置为当前节点。
实现如下:
/* filename: AvlTree.c */ static Position SingleRotationWithLeft(Position K2){ //左孩子的Height太大 Position K1 = K2->left; K2->left = K1->right; K1->right = K2; K2->height = Max(Height(K2->left), Height(K2->right)) + 1; K1->height = Max(Height(K1->left), Height(K2))+1; return K1; }
2、right-right case
这种情况和与前一种没有本质差别,这里仅仅附上图示和代码
// filename: Avltree.c static Position SingleRotationWithRight(Position K2){ //右孩子的Height太大,且大的分支在其右孩子 Position K1 = K2->right; K2->right = K1->left; K1->left = K2; K2->height = Max(Height(K2->left), Height(K2->right)) + 1; K1->height = Max(Height(K1->right), K2->height)+1; return K1; }
3、left-right case
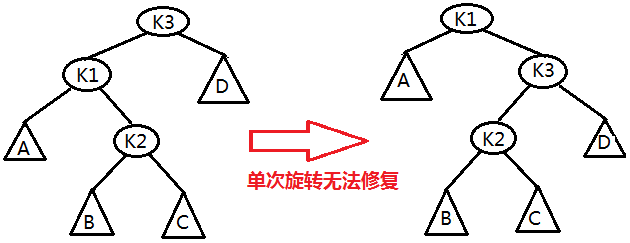
这种情况下,使用单次旋转后,可以看出当前节点(K1)仍然是不平衡的,因此我们需要进行两次旋转。旋转方法见图
等价于
这里使用了两次单旋转,先旋转K1和K2,再把K2置为当前节点。(通过图可以直观地看出K1->element < K2->element < K3->element)
// filename: Avltree.c static Position DoubleRotationWithLeft(Position K2){ // 左孩子太大,且大的分支在左孩子的右孩子上 K2->left = SingleRotationWithRight(K2->left); K2 = SingleRotationWithLeft(K2); return K2; }
4、right-left case
这种情形与情形3类似,不多解释,代码如下
// filename: Avltree.c static Position DoubleRotationWithRight(Position K2){ //右孩子太大,且大的分支是右孩子的左孩子 K2->right = SingleRotationWithLeft(K2->right); K2 = SingleRotationWithRight(K2); return K2; }
这四种旋转实现了平衡AVL树的功能,下面就插入元素分情况进行讨论。
如果T为空树,则插入比较简单,直接分配内存,并存储即可。如果T不为空树,则需要分情况讨论。这里再强调一次,
“在插入之前,AVL树中每个节点都是平衡的,插入元素以后,可能会导致 插入节点到根节点路径上的节点的平衡发生改变,而插入节点的子节点的平衡不变。沿着这条路径上行,对路径上的每个节点,检查其平衡状态,修正不平衡的节点,修正height,一直检查和修正到root节点。最后可以得到的是一棵平衡的AVL树。”
每个节点的平衡状态是由其左右子节点的高度差决定的,使用递归可以保证更新完子节点以后,上溯到父节点进行检查更新。
// filename: Avltree.c AvlTree Insert(double X, AvlTree T){ if(T==NULL){ // T 为空树 T = (AvlTree)malloc(sizeof(struct AvlNode)); if(T==NULL){ fprintf(stderr, "no space available!\n"); abort(); }else{ T->element = X; T->left = T->right = NULL; T->height = 0; } }else if(X<T->element){ T->left = Insert(X, T->left); if(Height(T->left) - Height(T->right)==2){ if(X<T->left->element) // X被插入到其左孩子的左子树中,left-left case T = SingleRotationWithLeft(T); else // X被插入到其左孩子的右子树中,left-right case T = DoubleRotationWithLeft(T); } }else if(X>T->element){ T->right = Insert(X, T->right); if(Height(T->right)-Height(T->left)==2){ if(X<T->right->element) // X被插入到右孩子的左子树中, right-left case T = DoubleRotationWithRight(T); else // X 被插入到其右孩子的右子树中, right-right case T = SingleRotationWithRight(T); } } // else if x== T->left->element, no need to know T->height = Max(Height(T->left),Height(T->right)) + 1; // 更新节点的高度 Max()为辅助函数 return T; }
六、实现删除
节点的删除比Insert麻烦一些,我们分情形处理。
- T为空树
- 要删除的元素不存在
- 要删除的元素位于叶子节点上
- 要删除的元素位于非叶子节点上
情形1 和情形2不需要太多处理,直接返回T;情形3则需要递归删除,并逐级上溯纠正树的平衡性;情形4比较复杂,这里将详细讨论。
假设要删除的节点为 a,如果a->left 或者 a->right为空树,则将 a = a->right(假设a->left==NULL), 释放原来a节点的空间,即可。然后逐个上溯到父节点,并调整其平衡性。如果 a的左右子树均不为空,则用其右子树的最小值取代 a中的值(a->element = FindMin(a->right)),递归删除右子树的最小值,然后调整a的平衡。最后逐个上溯到父节点,并调整其父节点的平衡性。
if(!T->left){ // 第一种情况: 左子树为NULL, 删除后需要重新计算高度(减一),但不需要调节平衡 pos = T; T = T->right; free(pos); }else if(!T->right){ //第二种情况:右子树为NULL,删除后需要重新计算高度(减一),但不需要调节平衡 pos = T; T = T->left; free(pos); }else{ // 第三种情况,左右子树均不为空 // 用右子树的最小值代替X,删除右子树最小值,并调节其平衡 pos = FindMin(T->right); T->element = pos->element; Delete(pos->element, T->right); // 递归删除最小值,计算高度,并调节平衡至 T->right // 但无法保证 T 的平衡,因此需要调节 if(Height(T->left) - Height(T->right)==2){ if(Height(T->left->right)-Height(T->left->left)==1) // left-right型 T = DoubleRotationWithLeft(T); else T = SingleRotationWithLeft(T); // left-left型 } }
Delete的全部实现如下:
AvlTree Delete(double X, AvlTree T){ Position pos; if(!T) return NULL; // when T ==NULL // 递归删除 if(X<T->element){ T->left = Delete(X, T->left);// 删除后,左子树元素个数减少,可能为 NULL if(Height(T->right)-Height(T->left)==2){ // 平衡被打破,右子树高度过高 if(T->left==NULL){ // need to identify them if(T->right->right==NULL) T = DoubleRotationWithRight(T); else T = SingleRotationWithRight(T); }else if(X<T->left->element) // X小于左子树的元素,为 left-right型 T = DoubleRotationWithLeft(T); else // X 大于左子树的元素,左子树的右子树的元素被删除,为left-left型 T = SingleRotationWithLeft(T); } }else if(X>T->element){ T->right = Delete(X, T->right); //删除后,右子树的元素个数减少, 可能为 NULL if(Height(T->left)-Height(T->right)==2){ //平衡被打破,左子树高度过高 if(T->right==NULL){ //left-left or left-right if(T->left->left==NULL) T = DoubleRotationWithLeft(T); else T = SingleRotationWithLeft(T); }else if(X<T->right->element) //X小于右子树元素,,为right-right型 T = SingleRotationWithRight(T); else //X 大于右子树元素,为right-left型 T = DoubleRotationWithRight(T); } }else{ // X == T->element if(!T->left){ // 第一种情况: 左子树为NULL, 删除后需要重新计算高度(减一),但不需要调节平衡 pos = T; T = T->right; free(pos); }else if(!T->right){ //第二种情况:右子树为NULL,删除后需要重新计算高度(减一),但不需要调节平衡 pos = T; T = T->left; free(pos); }else{ // 第三种情况,左右子树均不为空 // 用右子树的最小值代替X,删除右子树最小值,并调节其平衡 pos = FindMin(T->right); T->element = pos->element; Delete(pos->element, T->right); // 递归删除最小值,计算高度,并调节平衡至 T->right // 但无法保证 T 的平衡,因此需要调节 if(Height(T->left) - Height(T->right)==2){ if(Height(T->left->right)-Height(T->left->left)==1) // left-right型 T = DoubleRotationWithLeft(T); else T = SingleRotationWithLeft(T); // left-left型 } } } // things does not work when T ==NULL if(T) T->height = Max(Height(T->left),Height(T->right)) + 1; return T; }
参考引用: 《数据结构与算法分析--C语言描述》