MDX之平移与旋转(2)
简介
======================================================
昨天我发过了平移的一篇文章,就有人说都有现存的算法存在了,不错,我要提醒一下,我并不是什么技术高超的学者,
或者说是某某研究员,那么我的算法怎么来呢,有人说过天下文章一大抄,看你会抄不会抄,不知道大家有没有去过那些
论文网站,有没有去那里找过什么论文,反正我是常去的,你去了你就会发现,他们的那些很多算法也是别人已经做过,
已经写过的。
我发在这里也只是想起到一种提醒的作用,要说让我自己想一个什么高深的算法,我自认现在还没有那个水平。
======================================================
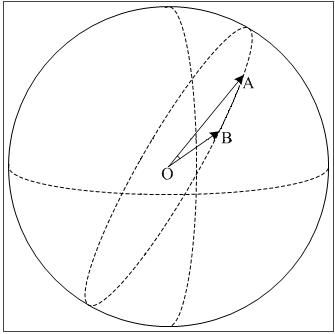
首先,在MDX中要通过鼠标的旋转就知道,鼠标这时的移动并不是在一个平面内移动,而是在一个半球内移动的。
就象上图中的从A到B点是按照圆的轨迹在移动,而不是按直线由A到B的。
旋转之所有叫旋转那就要有旋转轴和旋转角,旋转轴也就是平面OAB的法向量,平面的法向量有公式可以求的,旋转角
一样也有公式可以求:
n=OA×OB
α=ACOS((OA*OB)/(|OA|*|OB|))
在程序中旋转角(α)可以设置为2倍,这样如果用鼠标点击视图的左中边缘,然后拖动至视图的右中边缘,则可实现
模型以y 轴为旋转轴的360旋转,也就是一周。
现在的问题就成了求A,B两点坐标的问题了,那么这两点的坐标怎么样的确定呢,注意有两种情况:
还 有一个问题就是R的大小,R一般会设置成为窗口宽度的一半;
到此要解决的问题除了一个问题也就差不多都解决了,那个问题下面再说,我将代码copy到下面我在一句句说。。
2 Vector3 preVector = new Vector3(); // 前一次鼠标与中心点的向量
3 preVector.X = _posLast.X - radius; //A点坐标
4 preVector.Y = _posLast.Y - radius;
5 float square = radius * radius - preVector.X * preVector.X - preVector.Y * preVector.Y;
6 if (square <= 0 ) //前面说到的两tk
7 {
8 square = 0 ;
9 preVector.Z = 0 ;
10
11 preVector.X = preVector.X / preVector.Length();
12 preVector.Y = preVector.Y / preVector.Length();
13 }
14 else
15 {
16 preVector.Z = ( float )Math.Sqrt(square);
17
18 preVector.X = preVector.X / radius; // 单位化
19 preVector.Y = preVector.Y / radius;
20 preVector.Z = preVector.Z / radius;
21 }
22
23 Vector3 curVector = new Vector3(); // 现在鼠标与中心点的向量
24 curVector.X = e.X - radius; //A点坐标
25 curVector.Y = e.Y - radius;
26 square = radius * radius - curVector.X * curVector.X - curVector.Y * curVector.Y;
27 if (square <= 0 )
28 {
29 square = 0 ;
30 curVector.Z = 0 ;
31
32 curVector.X = preVector.X / curVector.Length();
33 curVector.Y = curVector.Y / curVector.Length();
34 }
35 else
36 {
37 curVector.Z = ( float )Math.Sqrt(square);
38
39 curVector.X = curVector.X / radius;
40 curVector.Y = curVector.Y / radius;
41 curVector.Z = curVector.Z / radius;
42 }
43
44 if (preVector == curVector)
45 return ;
46
47 Vector3 crossVector = Vector3.Cross(preVector, curVector);
48 float alpha = ( float )Math.Acos(Vector3.Dot(preVector, curVector) / (preVector.Length() * curVector.Length()));
49
50 _matrixRotation.Multiply(Matrix.RotationAxis(crossVector, alpha * 2 ));
这里我将最后的三句拿出来:
44-47:为什么要有这两句?这个可是为个算法里面的一个比较关键的地方, 这个算法有一点小问题就是当OA与OB
也就是preVector与curVector相隔非常小甚至相等的时候,大家想想会发生什么事情,想想Vector3.Cross()这个函数
是干什么的,如果上面两者相等会发生什么,这个就是我在做的时候就找了好久才找到的这个缺陷 ,开始我还以为是
算法本身有问题,就想了很多别的算法,绕了一大圈才找到这个。
48:求两者之间的角度
50:旋转2倍的角度(个人习惯),这里也要注意是每一次的旋转都要累加到一起来,matrixRotation就起到了累加器的
作用,并且还要是右乘上现在的旋转量,不是左乘。
好了,现在这个也就说完了,其实也比较的简单,其实技术就象我们老师说的一样,技术就是一张纸,在捅破之前非常
神秘,捅破之后就一钱不值了。