吴昊品游戏核心算法 Round 18 —— 吴昊教你玩Zen Puzzle Garden

  

  如果你认为无法因为玩一个电脑游戏而达到精神的顿悟，你可能是正确的。不过你完全可以试着解决一个禅宗花园发生的难题，从而达到静心的精神状态。

 
  这个游戏是获得2003年独立游戏节提名的精品游戏，在注重游戏画面和特效的今天，很多人无法接触到和了解这个游戏深刻内涵，特别推荐小游戏玩家来挑战这个禅宗花园的难题。

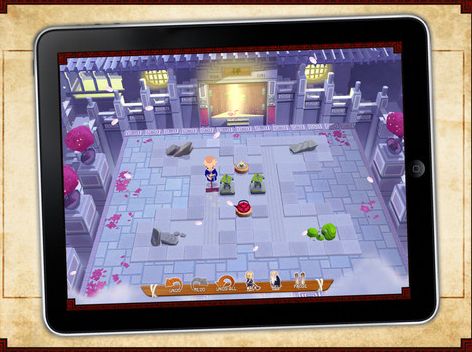
  如 图，这就是那个2003年的电脑游戏的截图，其挂卡的设计我在具体的AI实现中会说到，其实该游戏的关卡已经被证明是NP完全的（我在Round 14中也阐述过类似的关卡设计问题，也就是推箱子的关卡设计，一个有挑战的推箱子关卡往往被设计成指数级别的复杂度）。由于当时的智能手机并没有发达到如 今的地步，所以该游戏最初是在电脑端进行的单机游戏。

  如今，该游戏已经被安置到手机游戏的银屏上，比如这款基于ipad平台开发的小游戏，大有昔日的魂斗罗重登PS2之感啊！

 

  这里，注意到下角有一些辅助工具，这些都是一些AI小应用，自动退回，自动步进，以及让“智慧老人”指引你找到一条路径等等。可以看到，在手机端的改进版中，形状已经不是规则的矩形了，这也给AI的设计者提出了更大的挑战。

  关于游戏挂卡的NP完全证明，我在道客巴巴找到了一篇还没有被翻译出来的英文文献，我会和同学一起翻译，并在这一期Round给出。

 

  游戏的规则

  我 这里截取费恩曼在他的《费恩曼物理学讲义》中的一段话：研究物理学就好比研究两个绝世高手下棋，往往先要破解这个游戏的规则，这其实比较容易做到，但是， 我们在这个基础之上，还要想一想，他们是为什么要那么下棋？这就是要破解他们基于这一规则所制定的策略，这往往就是难上加难了，我们可以理解为模拟算法和 AI算法的区别。而且，往往最简单的规则的游戏会蕴含着最深奥的策略，比如围棋。

 

  如图(a),(b),(c),一个分块的矩形中间夹着几个石头，一个小人在上面行走。准确地说，应该是滑行吧，当他碰到石头的时候，就可以考虑换一个方向 进行滑动。每次滑行道离开这个沙场位置。我们最终的目标（goal）是将整个没有石头的沙子都恰好走过一遍（这里的恰好走过一遍的意思是：经过的沙地就不 允许再经过了），而且，这个小人在执行了这个过程之后，最终应该出现在沙子的外面。

  （如图，这是Zen Puzzle Garden目前的官方网站，为一个经典的游戏设置一个官网也是必须的事情）

 

  我们设计一款AI，可以再20s之内至少返回一个合理解（无解的情况暂时不考虑），将游戏的界面大小设计为12*12的模式，输入为一个界面，其中0来标记空地，1标记石子。输出的第一行为需要行走的轮数，后面为每一轮的具体步骤。

  该问题可以考虑为“吴昊系列Round 16——龙系道馆”的延伸，我们的主角还是采用“滑动”的模式，只是这一次不同之处在于，每一个格子走过之后就不允许再走了，所以，需要用一个visit 数组进行标记。而且，最后的游戏目标是恰好一次扫描到最有的格子，而不是到达一个目的地，所以，异常麻烦，源码我用的是Pengjiajun(NOI) 的，这里注明一下，有些地方还是木有看懂，他使用了三个函数，进行如下的调用：

  bfs()判断每一块小方形所能延拓的空地的总数(除开那个小方块本身)。

  bool dfs(int a[],pp nw,int ndeep)判断这个游戏是否存在一个解，如果搜索到了，则输出第一个搜索到的解。

  bool t_dfs(int a[],int id1,int id2,int na[],int dir,pp now,int deep,int ndeep)以一个固定的点，固定的步进度进行深度优先搜索，这是一个递归的函数，直到找到一个满足条件的解，该函数是dfs函数的子函数。

  另外，设置了数组a[]，利用30进制进行记录，应该是对空间的一个优化吧，暂时还木有搞得很明白。

   

  1 #include<iostream>
  2  #include<cstdlib>
  3  #include<algorithm>
  4  #include<cmath>
  5  #include<cstring>
  6  #incude<stdio.h>
  7  #include<map>
  8  #include<vector>
  9   using  namespace std;
 10  
 11  vector< int> adj[ 6][ 999997];
 12  
 13   int r,c,cnt;
 14   int MOD= 999997;
 15  
 16   // 这里定义方向向量，便于搜索 
 17    int dirx[]={- 1, 1, 0, 0};
 18   int diry[]={ 0, 0,- 1, 1};
 19  
 20   // 定义一个结构体，存储地图 
 21    struct pp
 22  {
 23     bool mat[ 20][ 20];       
 24  };
 25  
 26   struct bl
 27  {
 28     int num;
 29     short list[ 145][ 2];
 30     bool  operator <( const bl &temp)  const
 31    {
 32       return num<temp.num;     
 33    }       
 34  };
 35  
 36  pp nw;
 37  
 38   struct qq
 39  {
 40     int id1,id2;       
 41  };
 42  
 43  qq list[ 200],queue[ 200];
 44  
 45   // 这里标记是否经历过 
 46    bool visit[ 13][ 13];
 47  
 48   int f[ 20][ 20],temp1,temp2,temp,ans[ 200][ 200][ 2],num[ 200],cont;
 49  
 50   bool t_dfs( int a[], int id1, int id2, int na[], int dir,pp now, int deep, int ndeep);
 51   bool dfs( int a[],pp nw, int ndeep);
 52  
 53   void bfs( int id1, int id2,pp nw)
 54  {
 55     int i,j,s,p,q;
 56     // 将这个空白方块入队列，并标记为已经访问 
 57     queue[ 0].id1=id1;
 58    queue[ 0].id2=id2;
 59    visit[id1][id2]= true;
 60    temp1=temp2= 0;
 61    temp= 1;
 62     while(temp1<=temp2)
 63    {
 64       for(i=temp1;i<=temp2;i++)
 65      {
 66         // 分别对四个方向进行BFS 
 67          for(j= 0;j< 4;j++)       
 68        {
 69          id1=queue[i].id1+dirx[j];
 70          id2=queue[i].id2+diry[j];
 71           // 判断搜索的点是否越界
 72            if(id1>= 0&&id1<r&&id2>= 0&&id2<c)
 73          {
 74             // 如果延拓的这一点是空地而且未被访问的话
 75              if(visit[id1][id2]== false&&nw.mat[id1][id2]== 0)
 76            {
 77               // 标记为已访问，并且入队列
 78               visit[id1][id2]= true;
 79              queue[temp].id1=id1;
 80              queue[temp++].id2=id2;                                               
 81            }                                
 82          }                       
 83        }                  
 84      }            
 85       // 这里的含义是，去掉一个已经出队的点，增加新入队的点       
 86       temp1=temp2+ 1;
 87      temp2=temp- 1;
 88    }     
 89  }
 90  
 91   int main()
 92  {
 93     int i,j,ncnt,a[ 5];
 94    scanf( " %d%d ",&r,&c);
 95    cnt= 0;
 96    memset(f,- 1, sizeof(f));
 97     for(i= 0;i<r;i++)
 98    {
 99       for(j= 0;j<c;j++)
100      {
101        scanf( " %d ",&nw.mat[i][j]);
102         if(nw.mat[i][j]== 0)
103        {
104          list[cnt].id1=i;
105          list[cnt].id2=j;
106          f[i][j]=cnt++;                   
107        }                
108      }                
109    }
110    memset(num, 0, sizeof(num));
111    cont= 0;
112     // orz为真值，看是为true还是false 
113      int orz=dfs(a,nw, 0);
114     if(orz> 0)
115    {
116       // 总共需要行进几轮 
117       printf( " %d\n ",cont);
118       for(i= 0;i<cont;i++)
119      {
120         // 每一轮的行进步数 
121         printf( " %d: ",num[i]);
122         // 加1的原因是，那个数组是从0下标开始计数的 
123          for(j= 0;j<num[i];j++)
124          printf( "  (%d,%d) ",ans[i][j][ 0]+ 1,ans[i][j][ 1]+ 1);
125        printf( " \n ");                   
126      }         
127    }
128     return  0;    
129  }
130  
131   bool t_dfs( int a[], int id1, int id2, int na[], int dir,pp now, int deep, int ndeep)
132  {
133     int i,j,x,y,id,b[ 6];
134    ans[ndeep][deep][ 0]=id1;
135    ans[ndeep][deep][ 1]=id2;
136     // 将目前的点标记为石头，表明已经走过 
137     now.mat[id1][id2]= 1;
138     // 对已经选定好的方向进行搜索 
139     x=id1+dirx[dir];
140    y=id2+diry[dir];
141     if(x< 0||x>=r||y< 0||y>=c)
142    {
143       // 如果已经出界，记录答案 
144       ans[ndeep][deep+ 1][ 0]=x;
145      ans[ndeep][deep+ 1][ 1]=y;
146      num[ndeep]=deep+ 2;
147       if(num[ndeep]> 3)
148      {
149         if(dfs(b,now,ndeep+ 1))
150           return  true;
151      }
152       // 不行的话，重新标记为空地 
153       now.mat[id1][id2]= 0;
154       return  false;                        
155    }
156     // 如果没有越界而且这里为空地的话，则可能满足题目条件 
157      if(now.mat[x][y]== 0)
158    {
159       // 搜索深度每次加深1个单位 
160        if(t_dfs(a,x,y,na,dir,now,deep+ 1,ndeep))  return  true;
161       // 否则，退回到原来的状态
162       now.mat[id1][id2]= 0;
163       return  false;                    
164    }     
165     // 如果不是空地的话，朝四个方向搜索 
166      else
167    {
168       for(i= 0;i< 4;i++)
169      {
170        x=id1+dirx[i];
171        y=id2+diry[i];
172         if(x< 0||x>=r||y< 0||y>=c)
173        {
174          ans[ndeep][deep+ 1][ 0]=x;
175          ans[ndeep][deep+ 1][ 1]=y;
176           if(num[ndeep]> 3)
177          {
178             if(dfs(b,now,ndeep+ 1))  return  true;                
179          }                        
180        }                
181         else  if(now.mat[x][y]== 0)
182        {
183           if(t_dfs(a,x,y,na,i,now,deep+ 1,ndeep))  return  true;     
184        }
185      } 
186       // 否则，将其重新标为空地，返回false
187       now.mat[id1][id2]= 0;
188       return  false;   
189    }
190  }
191  
192   bool dfs( int a[],pp nw, int ndeep)
193  {
194     int siz,value= 0,i,j,s= 0,cou= 0,na[ 5],b[ 6],id, in= 1000000000;
195    pp now;
196    bl block[ 20];
197    a[ 0]=a[ 1]=a[ 2]=a[ 3]=a[ 4]= 0;
198     // 利用一个数组模拟30进制存储 
199      for(i= 0;i<r;i++)
200    {
201       for(j= 0;j<c;j++)
202      {
203         if(nw.mat[i][j]== 0)
204        {
205           int id=f[i][j];
206          a[id/ 30]+=( 1<<(id% 30));                   
207        }                
208      }                  
209    }     
210     if(a[ 0]== 0&&a[ 1]== 0&&a[ 2]== 0&&a[ 3]== 0&&a[ 4]== 0)
211    {
212      cont=ndeep;
213       return  true;                                               
214    }
215     // 否则,按照键值存储一个状态 
216      for(i= 4;i>= 0;i--)
217      value=((( long  long)(( 1<< 30)%MOD)*( long  long)value)%MOD+a[i])%MOD;
218    siz=adj[ 0][value].size();
219     // 这是判断是否越出了五位的界么？这个逻辑实现的功能还没怎么看懂 
220      for(i= 0;i<siz;i++)
221    {
222       for(j= 0;j< 5;j++)
223      {
224         if(adj[j][value][i]!=a[j])  break;
225      }
226       if(j>= 5)  break;
227    }
228     if(i<siz)  return adj[ 5][value][i];    
229    memset(visit, false, sizeof(visit));
230     for(i= 0;i<r;i++)
231       for(j= 0;j<c;j++)
232      {
233         // 对于每一个还没有遍历，且为空地的地方，进行bfs扫描 
234          if(visit[i][j]== false&&nw.mat[i][j]== 0)
235        {
236          bfs(i,j,nw);
237           // 每次新增的块 
238           block[cou].num=temp;
239           // 将对每一点搜索的新增的块都加入到list中 
240            for(s= 0;s<temp;s++)
241          {
242            block[cou].list[s][ 0]=queue[s].id1;
243            block[cou].list[s][ 1]=queue[s].id2;
244          }
245          cou++;
246        }
247      }
248     // 对每一个块进行分析 
249      for(i= 0;i<cou;i++)
250    {
251       // 利用变量orz存储由这个方块延拓的遇到边界的次数（神牛就是神牛，变量名都那么精彩） 
252        int orz= 0;
253       // 对那一块所有新增加的块进行分析 
254        for(j= 0;j<block[i].num;j++)
255      {
256         if(block[i].list[j][ 0]== 0)
257          orz++;
258         else  if(block[i].list[j][ 0]==r- 1)
259          orz++;
260         else  if(block[i].list[j][ 1]== 0)
261          orz++;
262         else  if(block[i].list[j][ 1]==c- 1)
263          orz++;
264      }
265       // 得到块数最小的点 
266        if( in>block[i].num)
267      {
268         in=block[i].num;
269        id=i;
270      }
271       // 如果只能触及到一个边界，那么是不行的 
272        if(orz<= 1)  return  false;
273      }
274    }
275       // 这里给出了我们的AI策略，每次选取延拓方块最小的，这样最不容易导致出现"石头阻挡"或者"经历过的点，绕不回来"的毛病 
276       swap(block[id],block[ 0]);
277       for(i= 0;i<block[ 0].num;i++)
278      {            
279         // 对块延拓出的边界点进行处理，广度搜索，并存储在a[]中               
280          if(block[ 0].list[i][ 0]== 0)
281        {
282          memset(na, 0, sizeof(na));
283          now=nw;
284          num[ndeep]= 0;
285          ans[ndeep][num[ndeep]][ 0]=- 1;
286          ans[ndeep][num[ndeep]++][ 1]=block[ 0].list[i][ 1];
287           // 如果这条路径可达的话 
288            if(t_dfs(a,block[ 0].list[i][ 0],block[ 0].list[i][ 1],na, 1,now, 1,ndeep))
289          {
290             for(j= 0;j< 5;j++)
291              adj[j][value].push_back(a[j]);
292            adj[ 5][value].push_back( 1);
293             return  true;
294          }         
295        }
296         if(block[ 0].list[i][ 0]==r- 1)
297        {                                                                          
298          memset(na, 0, sizeof(na));
299          now=nw;
300          num[ndeep]= 0;
301          ans[ndeep][num[ndeep]][ 0]=r;
302          ans[ndeep][num[ndeep]++][ 1]=block[ 0].list[i][ 1];
303           if(t_dfs(a,block[ 0].list[i][ 0],block[ 0].list[i][ 1],na, 0,now, 1,ndeep))
304          {
305             for(j= 0;j< 5;j++)
306              adj[j][value].push_back(a[j]);
307            adj[ 5][value].push_back( 1);
308             return  true;
309          }         
310        }
311         if(block[ 0].list[i][ 1]== 0)
312        {                        
313          memset(na, 0, sizeof(na));
314          now=nw;
315          num[ndeep]= 0;
316          ans[ndeep][num[ndeep]][ 0]=block[ 0].list[i][ 0];
317          ans[ndeep][num[ndeep]++][ 1]=- 1;
318           if(t_dfs(a,block[ 0].list[i][ 0],block[ 0].list[i][ 1],na, 3,now, 1,ndeep))
319          {
320             for(j= 0;j< 5;j++)
321              adj[j][value].push_back(a[j]);
322            adj[ 5][value].push_back( 1);
323             return  true;
324          }
325        }
326         if(block[ 0].list[i][ 1]==c- 1)
327        {                   
328          memset(na, 0, sizeof(na));
329          now=nw;
330          num[ndeep]= 0;
331          ans[ndeep][num[ndeep]][ 0]=block[ 0].list[i][ 0];
332          ans[ndeep][num[ndeep]++][ 1]=c;
333           if(t_dfs(a,block[ 0].list[i][ 0],block[ 0].list[i][ 1],na, 2,now, 1,ndeep))
334          {
335             for(j= 0;j< 5;j++)
336              adj[j][value].push_back(a[j]);
337            adj[ 5][value].push_back( 1);
338             return  true;
339          }
340        }
341      }
342       for(j= 0;j< 5;j++)
343        adj[j][value].push_back(a[j]);
344      adj[ 5][value].push_back( 0);
345       return  false;
346  }
347  
348  
349  
350  
351  
352  

   《禅宗花园》ipad图标