吴昊品游戏核心算法 Round 17 —— 吴昊教你玩拼图游戏（15 puzzle）

  以上，8--puzzle转化为了15--puzzle，状态数增加了，游戏的难度也加大了，AI也更加具有挑战性。

  现在，我们的PUZZLE的目标状态变成了如下的情况，游戏的规模由3*3变成了4*4，这么一变不得了，状态数由O(9!)变成了O（16!），由于n!的增长速率在NP中都是变态的，所以，即使是从9增加到了16，规模都会大许多，这样的话，优化的难度也大大增加了。

 

 

  这里，我们先不慌着再AI，因为，15--puzzle的AI设计将更为复杂，因为考虑到状态变得更多，需要更多更好的优化才可以。我们不妨在考虑移动的过程AI之前，先考虑一种更为简单的判定性的AI，也就是我们玩的这个游戏是否必定存在一个解（如果有解的话，肯定存在最优解，当然，次优解是无穷多的，你可以将空白方块绕一圈，这样，路径的长度又加了4），那么，如何判定呢？

15数码的解的存在性判定AI

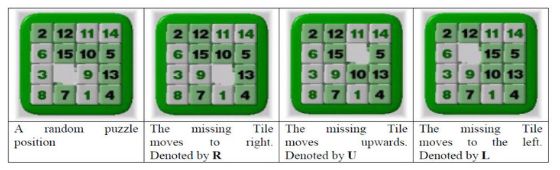
  我们考虑到如下的事实，也就是：空格（0）往左或者往右则置换是不变的。如果往上或者往下，必定交换偶数个数，所以逆序数的奇偶性不变。这个很容易理解，左换和右换，15数码的顺序不会有丝毫的改变，如果是上下交换的话，对应的那两个数和原来那两个所在位置的数的奇偶性不会有丝毫的改变，那么两者取并，我们可以得出，其充要条件可以描述为：只要比较比较其逆序数的奇偶性就可以了。

 

 

    Solve:

   Highlights:我们输入一个游戏的状态，可以看到是否可以变为目标状态，同样的思路可以运用于8--puzzle问题。 

 

 1  #include<iostream>
 2   using  namespace std;
 3 
 4   int cur_num[ 16]; 
 5  
 6   // 位置对应的数字 
 7    int des_num[ 16]={ 1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 0, 15, 14, 13};
 8 
 9   bool solvable()
10  {
11     int ni1= 0,ni2= 0;
12     // 找到当前状态的逆序对的总数
13      for( int i= 0;i< 16;i++)
14    {
15       if(cur_num[i]== 0)  continue;
16       for( int j=i+ 1;j< 16;j++)
17      {
18         if(cur_num[j]== 0)  continue;
19         if(cur_num[i]>cur_num[j])
20        {
21          ni1++;
22        }
23      }
24    }
25     for( int i= 0;i< 16;i++)
26    {
27       if(des_num[i]== 0)  continue;
28       for( int j=i+ 1;j< 16;j++)
29      {
30         if(des_num[j]== 0)  continue;
31         if(des_num[i]>des_num[j])
32        {
33          ni2++;
34        }
35      }
36    }
37     // 如果奇偶性相同的话，则说明是可以互相变化得到的
38      if(((ni1-ni2)& 1)== 0)  return  true;
39     return  false;
40  }
41 
42   int main()
43  {
44     int t,a;
45     // 读入样例的总数，a用来载入数据 
46     cin>>t;
47     while(t--)
48    {
49       // 考虑到逆序数，这里用这种方式读数据
50        for( int i= 0;i< 4;i++)
51      {
52        cin>>a;
53        cur_num[i]=a;
54      }
55       for( int i= 7;i> 3;i--)
56      {
57        cin>>a;
58        cur_num[i]=a;
59      }
60       for( int i= 8;i< 12;i++)
61      {
62        cin>>a;
63        cur_num[i]=a;
64      }
65       for( int i= 15;i> 11;i--)
66      {
67        cin>>a;
68        cur_num[i]=a;
69      }
70       if(solvable()) cout<< " YES\n ";
71       else cout<< " NO\n ";
72    }
73     return  0;
74  }
75 
76   

 

 

 

   15数码问题的解的存在性定理的严谨证明(Kobe给出的)

//这里指的是网上的那位Kobe大神，而不是NBA上面的科比

设0当前的位置为（x，y）；起始位置为（4,4）;

每次0移动后，定义dist=abs(x-4)+abs(y-4);

定义perm为逆序对的数目；

记s=perm+dist；

则有结论：每次0的位置移动后，s的奇偶性保持不变。

证明过程如下：

0每次移动后，不管方向如何，dist只会加1或减1，所以dist的奇偶性会改变。

要证明s的奇偶性保持不变，只要证明，perm的奇偶性改变。

对于0向左移动，开始的的序列为:

a[1],a[2].....a[i],0,a[i+2],...a[16];

移动后序列为：

a[1],a[2].....0,a[i],a[i+2],...a[16];

很明显，perm减1，奇偶性改变。

对于0向右移动同理可证perm奇偶性改变。

对于0向下移动，

开始的序列为：

a[1],a[2]...0,a[i],a[i+1],a[i+2],a[i+3]...a[16];

移动后序列为：

a[1],a[2]...a[i+3],a[i],a[i+1],a[i+2],0...a[16];

只要考虑

{0,a[i],a[i+1],a[i+2],a[i+3]}

{a[i+3],a[i],a[i+1],a[i+2],0}

的逆序对之差即可，很明显，

对于包含0的逆序对数目改变为4。

对于a[i],a[i+1],a[i+2],改变为1，

4+1+1+1=7为奇数。

所以结论成立。

 

  15数码问题的解的过程性阐述AI —— 这里用四种方法来阐述

Highlights: 太多了，有些还利用了论文中的相关观点，BFS,DFS比较一般，后面两种（A*和IDA*用到了启发式搜索，引入了一些主观性），可以说，亮点很多，比如闭合集和开环集，利用这种方式免去了8--puzzle问题中的用数组来标记访问节点的办法，这样可以避免了严重的超内存

 

  1 #include <iostream>
  2 
  3  #include <cstring>
  4 
  5  #include <limits>
  6 
  7  #include <vector>
  8 
  9  #include <queue>
 10 
 11  #include <stack>
 12 
 13  #include < set>
 14 
 15  #include <map>
 16 
 17         
 18 
 19   using  namespace std;
 20 
 21  
 22 
 23   // 开辟一个4*4的布局        
 24 
 25   #define SQUARES 4
 26 
 27   // 将局面转换成整数的基数，类似于康托扩展
 28 
 29   #define BASE 16                      
 30 
 31   // DFS的最大搜索深度
 32 
 33   #define DEPTHBOUND 30              
 34 
 35   // 路径的最大长度（假设不会超过50，为了让数组可以装填下）
 36 
 37   #define STEPSBOUND 50                
 38 
 39         
 40 
 41   #define MOVE_LEFT (-1)
 42 
 43   #define MOVE_RIGHT 1
 44 
 45   #define MOVE_UP (-SQUARES)
 46 
 47   #define MOVE_DOWN SQUARES
 48 
 49   #define MOVE_NONE 0
 50 
 51  
 52 
 53   // 开启一个曼哈顿距离的预算表       
 54 
 55   int manhattan[SQUARES * SQUARES][SQUARES * SQUARES];     
 56 
 57   // 后续的移动
 58 
 59   int move[SQUARES];     
 60 
 61         
 62 
 63   // 一个描述局面信息的数据结构
 64 
 65   struct node
 66 
 67  {
 68 
 69     // 利用vector容器装填当前的状态
 70 
 71    vector < int> state;    
 72 
 73     // 装填一个最优解，就是行走的序列
 74 
 75     int moves[STEPSBOUND];
 76 
 77     // 当前的深度            
 78 
 79     int depth;                    
 80 
 81     // 当前的节点的估计值（用于启发式搜索）
 82 
 83     int score;                     
 84 
 85     // 空格的位置
 86 
 87     int blank;                     
 88 
 89  };
 90 
 91         
 92 
 93   // 优先队列的比较函数,分值较小的在优先队列的前端(运算符重载)
 94 
 95   bool  operator<(node x, node y)
 96 
 97  {
 98 
 99     return x.score > y.score;
100 
101  }
102 
103         
104 
105   // 求绝对值
106 
107   int absi( int x)
108 
109  {
110 
111     return x >=  0 ? x:(-x);
112 
113  }
114 
115         
116 
117   // 判断给定局面是否可解,利用上述的策略，就是逆序对的奇偶性原则
118 
119   bool solvable(vector < int> tiles)
120 
121  {
122 
123     int sum =  0, row;
124 
125     for ( int i =  0; i < tiles.size(); i++)
126 
127    {
128 
129       int tile = tiles[i];
130 
131            if (tile ==  0)
132 
133           {
134 
135             row = (i / SQUARES +  1);
136 
137              continue;
138 
139      }
140 
141       for ( int m = i; m < tiles.size(); m++)
142 
143              if (tiles[m] < tile && tiles[m] !=  0)
144 
145               sum++;
146 
147    }
148 
149     return !((sum + row) %  2);
150 
151  }
152 
153  
154 
155   /*   
156 
157     得到当前局面的后继走法。MOVE_LEFT = 向左移动空滑块，MOVE_RIGHT = 向右移动空滑块，
158 
159     MOVE_UP = 向上移动空滑块，MOVE_DOWN = 向下移动空滑块
160 
161    */
162 
163  
164 
165   void valid_moves(node &current)
166 
167  {
168 
169     // 获取后继走法，但除去退回到该状态的上一步的走法
170 
171           int last_move = MOVE_NONE;
172 
173           // 搜索深度确定之后，就可以确定最后一步在哪里了
174 
175           if (current.depth)
176 
177                    last_move = current.moves[current.depth -  1];
178 
179          memset(move, MOVE_NONE,  sizeof(move));
180 
181           // 尝试四个方向，这四个方向的移动都有范围的合法性制约
182 
183           if (current.blank % SQUARES >  0 && last_move != MOVE_RIGHT)
184 
185            move[ 0] = MOVE_LEFT;;
186 
187           if (current.blank % SQUARES < (SQUARES -  1) && last_move != MOVE_LEFT)
188 
189            move[ 1] = MOVE_RIGHT;
190 
191           if (current.blank / SQUARES >  0 && last_move != MOVE_DOWN)
192 
193            move[ 2] = MOVE_UP;
194 
195           if (current.blank / SQUARES < (SQUARES -  1) && last_move != MOVE_UP)
196 
197            move[ 3] = MOVE_DOWN;
198 
199  }
200 
201         
202 
203   // 将棋面状态转换为一个整数(保证每一个状态都有一个唯一的最优值)
204 
205  unsigned  long  long key(vector < int> &tiles)
206 
207  {
208 
209    unsigned  long  long key =  0;
210 
211     for( int i =  0; i < tiles.size(); i++)
212 
213      key = key * BASE + tiles[i];
214 
215     return key;
216 
217  }
218 
219         
220 
221   // 从局面 current 执行 move 所指定的走法
222 
223  node execute(node &current,  int move)
224 
225  {
226 
227    node successor;
228 
229     // 走法步骤设定
230 
231    memcpy(successor.moves, current.moves,  sizeof(current.moves));
232 
233    successor.depth = current.depth+ 1;
234 
235    successor.moves[current.depth] = move;
236 
237     // 局面状态设定,按 move 指定方向移动，交换空滑块位置(这里等于是交换两个方块的位置)
238 
239    successor.state = current.state;
240 
241    successor.blank = current.blank+move;
242 
243    successor.state[current.blank] = successor.state[successor.blank];
244 
245    successor.state[successor.blank] =  0;
246 
247     return successor;
248 
249  }
250 
251  
252 
253   /*
254 
255     由于 h*（n） 在算法中非常关键，而且它是高度特化的，根据问题的不同而不同，所以需要找到一个合适
256 
257     的 h*（n） 函数是比较困难的，在这里使用的是每个方块到其目标位置的曼哈顿距离之和，曼哈顿距离是
258 
259     该状态要达到目标状态至少需要移动的步骤数。g*（n） 为到达此状态的深度，在这里采用了如下评估函
260 
261     数： f*（n） = g*（n） + 4 / 3 * h*（n），h*（n） 为当前状态与目标状态的曼哈顿距离，亦可
262 
263     以考虑计算曼哈顿配对距离。本题中实验了一下，效率比单纯曼哈顿距离要高，但比曼哈顿距离乘以适当系
264 
265     数的方法低。可参考：
266 
267     [Bernard Bauer，The Manhattan Pair Distance Heuristic for the 15-Puzzle，1994]
268 
269    */
270 
271  
272 
273   // 这里的评价函数综合地考虑到了曼哈顿距离和搜索的深度，所以比较完美
274 
275   int score(vector < int> &state,  int depth)
276 
277  {
278 
279     int hn =  0;
280 
281     for ( int i =  0; i < state.size(); i++)
282 
283       if (state[i] >  0)
284 
285        hn += manhattan[state[i] -  1][i];
286 
287     return (depth +  4 * hn /  3);
288 
289  }
290 
291         
292 
293   // 判断是否已达到目标状态。
294 
295   bool solved(vector <  int > &state)
296 
297  {
298 
299     // 考虑最后一个元素是否是0,首先考虑最后一个元素，其实起到了一种剪枝的作用
300 
301     if (state[SQUARES * SQUARES -  1] !=  0)
302 
303       return  false;
304 
305     for( int i =  0; i < SQUARES * SQUARES -  1; i++)
306 
307       if (state[i] != (i +  1))
308 
309          return  false;
310 
311     return  true;
312 
313  }
314 
315         
316 
317   // 找到局面状态的空滑块位置
318 
319   int find_blank(vector <  int > &state)
320 
321  {
322 
323     for( int i =  0; i < SQUARES * SQUARES; i++)
324 
325       if (state[i] ==  0)
326 
327              return i;
328 
329  }

 

 

 

 

  1   /*   
  2 
  3     [深度优先搜索]——DFS
  4 
  5     与广度优先搜索不同的是使用栈来保存开放集。对于移动步数较少（15步左右）时可以较快的得到解，但是
  6 
  7     随着解移动步数的增加，得到解的时间及使用的内存都会大大增加，所以对于本题来说，不是有效的解决办
  8 
  9     法。是否能得到解和解的深度限制有关，如果选择的深度不够大，可能不会得到解，若过大，将导致搜索时
 10 
 11     间成倍增加
 12 
 13    */
 14 
 15  
 16 
 17   bool solve_puzzle_by_depth_first_search(vector < int> tiles,  int directions[])
 18 
 19  {
 20 
 21     // 定义一个堆栈的节点
 22 
 23    node copy;
 24 
 25    copy.state = tiles;
 26 
 27    copy.depth =  0;
 28 
 29    copy.blank = find_blank(tiles);
 30 
 31     // 将移动的数组清空
 32 
 33    memset(copy.moves, MOVE_NONE,  sizeof(copy.moves));
 34 
 35     // 检测当前局面是否为已解决状态。
 36 
 37     if (solved(copy.state))
 38 
 39    {
 40 
 41      memcpy(directions, copy.moves,  sizeof(copy.moves));
 42 
 43            return  true;
 44 
 45    }
 46 
 47     // 将初始状态放入开放集中
 48 
 49    stack <node> open;
 50 
 51    open.push(copy);
 52 
 53     // 闭合集
 54 
 55     set <unsigned  long  long> closed;
 56 
 57     while (!open.empty())
 58 
 59    {
 60 
 61       // 处理开放集中的局面，并将该局面放入闭合集中
 62 
 63      node current = open.top();
 64 
 65           open.pop();
 66 
 67           closed.insert(key(current.state));
 68 
 69            // 获取该局面的后继走法，后继走法都会加入开放集中
 70 
 71           valid_moves(current);
 72 
 73            for ( int i =  0; i < SQUARES; i++)
 74 
 75           {
 76 
 77              if(move[i] == MOVE_NONE)
 78 
 79                continue;
 80 
 81              // 在当前局面上执行走法
 82 
 83             node successor = execute(current, move[i]);
 84 
 85              // 如果已经访问，尝试另外一种走法(利用闭合集来装填已经访问的路径，避免了用一个很大的数组来标识)
 86 
 87              if(closed.find(key(successor.state)) != closed.end())
 88 
 89                continue;
 90 
 91              // 记录求解中前一步走法，如果找到解，那么立即退出。否则的话在限制的
 92 
 93               // 深度内将其加入开放集   
 94 
 95              if(solved(successor.state))
 96 
 97             {
 98 
 99               memcpy(directions, successor.moves,  sizeof(successor.moves));
100 
101                      return  true;
102 
103        }
104 
105         // 将当前局面放入开放集中（这里对其深度进行一定程度的剪枝）
106 
107         if(successor.depth < DEPTHBOUND)
108 
109               open.push(successor);
110 
111       }
112 
113    }
114 
115     return  false;
116 
117  }

 

  

 

  1   /*   
  2 
  3     [广度优先搜索]——BFS
  4 
  5     对于移动步数较少（15步左右）时可以较快的得到解，但是随着解移动步数的增加，得到解的时间及使用的
  6 
  7     内存都会大大增加，所以对于本题来说，不是有效的解决办法
  8 
  9    */
 10 
 11  
 12 
 13   bool solve_puzzle_by_breadth_first_search(vector <  int > tiles,  int directions[])
 14 
 15  {
 16 
 17    node copy;
 18 
 19    copy.state = tiles;
 20 
 21    copy.depth =  0;
 22 
 23    copy.blank = find_blank(tiles);
 24 
 25    memset(copy.moves, MOVE_NONE,  sizeof(copy.moves));
 26 
 27     // 检测当前局面是否为已解决状态
 28 
 29     if(solved(copy.state))
 30 
 31    {
 32 
 33      memcpy(directions, copy.moves,  sizeof(copy.moves));
 34 
 35            return  true;
 36 
 37    }
 38 
 39     // 将初始状态放入开放集中
 40 
 41    queue < node > open;        
 42 
 43    open.push(copy);
 44 
 45     // 闭合集
 46 
 47     set < unsigned  long  long > closed;
 48 
 49     while (!open.empty())
 50 
 51    {
 52 
 53       // 处理开放集中的局面，并将该局面放入闭合集中
 54 
 55      node current = open.front();
 56 
 57           open.pop();
 58 
 59           closed.insert(key(current.state));
 60 
 61            // 获取该局面的后继走法，后继走法都会加入开放集中
 62 
 63           valid_moves(current);
 64 
 65            for ( int i =  0; i < SQUARES; i++)
 66 
 67           {
 68 
 69              if(move[i] == MOVE_NONE)
 70 
 71                continue;
 72 
 73              // 在当前局面上执行走法
 74 
 75             node successor = execute(current, move[i]);
 76 
 77              // 如果已经访问，尝试另外一种走法
 78 
 79              if(closed.find(key(successor.state)) != closed.end())
 80 
 81                continue;
 82 
 83              // 记录求解中前一步走法，如果找到解，那么立即退出 
 84 
 85              if(solved(successor.state))
 86 
 87        {
 88 
 89               memcpy(directions, successor.moves,  sizeof(successor.moves));
 90 
 91                return  true;
 92 
 93             }
 94 
 95              // 将当前局面放入开放集中
 96 
 97             open.push(successor);
 98 
 99      }
100 
101    }
102 
103     return  false;
104 
105  }

 

 

 

 

  1   /*   
  2 
  3     [A* 搜索]——楼天成之百度之星ASTAR
  4 
  5     深度优先搜索和宽度优先搜索都是盲目的搜索，并没有对搜索空间进行剪枝，导致大量的状态必须被检测，
  6 
  7     A* 搜索在通过对局面进行评分，对评分低的局面优先处理（评分越低意味着离目标状态越近），这样充分
  8 
  9     利用了时间，在尽可能短的时间内搜索最有可能达到目标状态的局面，从而效率比单纯的 DFS 和 BFS 要
 10 
 11     高，不过由于需要计算评分，故启发式函数的效率对于 A* 搜索至关重要，值得注意的是，即使较差的启
 12 
 13     发式函数，也能较好地剪枝搜索空间。对于复杂的局面状态，必须找到优秀的启发式函数才可能在给定时间
 14 
 15     和内存限制下得到解，如果给定复杂的初始局面，而没有优秀的启发式函数，则由于 A* 搜索会存储产生的
 16 
 17     节点，大多数情况下，在能找到解之前会由于问题的巨大状态数而导致内存耗尽
 18 
 19    */
 20 
 21  
 22 
 23   bool solve_puzzle_by_a_star(vector < int> tiles,  int directions[])
 24 
 25  {
 26 
 27    node copy;
 28 
 29    copy.state = tiles;
 30 
 31    copy.depth =  0;
 32 
 33    copy.blank = find_blank(tiles);
 34 
 35     // 这里记录各个状态的评分，分值越低越好
 36 
 37    copy.score = score(copy.state,  0);
 38 
 39    memset(copy.moves, MOVE_NONE,  sizeof(copy.moves));
 40 
 41     // A*搜索利用优先队列priority_queue容器来存储开放集 
 42 
 43    priority_queue < node > open; 
 44 
 45    open.push(copy);
 46 
 47     // 闭合集利用map容器进行映射
 48 
 49    map <unsigned  long  long,  int>closed;
 50 
 51     while (!open.empty())
 52 
 53    {
 54 
 55       // 删除评价值最小的节点，标记为已访问过
 56 
 57           node current = open.top();
 58 
 59           open.pop();
 60 
 61            // 将状态特征值和状态评分存入闭合集中(一个状态对应唯一的一个评分)
 62 
 63           closed.insert(make_pair<unsigned  long  long,  int> (key(current.state), current.score));
 64 
 65            // 如果是目标状态，返回
 66 
 67            if(solved(current.state))
 68 
 69           {
 70 
 71             memcpy(directions, current.moves, sizeof(current.moves));
 72 
 73              return  true;
 74 
 75           }
 76 
 77            // 计算后继走法，更新开放集和闭合集(4个方向搜索)
 78 
 79           valid_moves(current);
 80 
 81            for( int i =  0; i < SQUARES; i++)
 82 
 83           {
 84 
 85              if(move[i] == MOVE_NONE)
 86 
 87                continue;
 88 
 89         // 移动滑块，评价新的状态
 90 
 91             node successor = execute(current, move[i]);
 92 
 93              // 根据启发式函数对当前状态评分(根据状态很深度进行评分)
 94 
 95             successor.score = score(successor.state, successor.depth);
 96 
 97            
 98 
 99         /*
100 
101           A*算法的局限性：
102 
103                如果当前状态已经访问过，查看是否能够以更小的代价达到此状态，如果没
104 
105                有，继续，否则从闭合集中提出并处理。在深度优先搜索中，由于可能后面
106 
107                生成的局面评分较高导致进入闭合集，从栈的底端生成同样的局面，评分较
108 
109                低，但是由于较高评分的局面已经在闭合集中，评分较低的等同局面将不予
110 
111                考虑，这可能会导致深度搜索 “漏掉” 解
112 
113          */
114 
115            
116 
117         // 不断迭代，直到得到一个最优解                 
118 
119        map < unsigned  long  long,  int >::iterator it = closed.find(key(successor.state));
120 
121         if (it != closed.end())
122 
123             {
124 
125           if (successor.score >= (*it).second)
126 
127                        continue;
128 
129               closed.erase(it);
130 
131             }
132 
133              // 当前局面放入开放集中
134 
135             open.push(successor);
136 
137           }
138 
139    }
140 
141     return  false;
142 
143  }

 

 

   

/*   

   [IDA* 搜索]

   深度优先在内存占用方面占优势，但是由于没有剪枝，导致搜索空间巨大，A* 搜索虽然剪枝，但是由于存

   储了产生的每个节点，内存消耗较大。IDA* 搜索结合了两者的优势。IDA* 实质上就是在深度优先搜索的

   算法上使用启发式函数对搜索深度进行限制

  */

 

  bool solve_puzzle_by_iterative_deepening_a_star(vector <  int > tiles, int directions[])

 {

   node copy;

   copy.state = tiles;

   copy.depth =  0;

   copy.blank = find_blank(tiles);

   memset(copy.moves, MOVE_NONE,  sizeof(copy.moves));

        

    // 检测当前局面是否为已解决状态

    if(solved(copy.state))

   {

     memcpy(directions, copy.moves,  sizeof(copy.moves));

           return  true;

   }

  

    // 设定初始搜索深度为初始状态的评分

    int depth_limit =  0, min_depth = score(copy.state,  0);

    while( true)

   {

      // 获取迭代后的评分

           if(depth_limit < min_depth)

            depth_limit = min_depth;

           else

             // 开始搜索第一层

            depth_limit++;

          numeric_limits< int> t;

          min_depth = t.max();

           // 开始新的深度优先搜素，深度为 depth_limit

     stack < node > open;

          open.push(copy);

           while (!open.empty())

          {

            node current = open.top();

            open.pop();

             // 获取该局面的后继走法，后继走法都会加入开放集中

            valid_moves(current);

             for ( int i =  0; i < SQUARES; i++)

            {

               if (move[i] == MOVE_NONE)

                       continue;

          // 在当前局面上执行走法

                    node successor = execute(current, move[i]);

               // 记录求解中前一步走法，如果找到解，那么立即退出。否则的话在限制的深度内将其加入开放集   

                     if(solved(successor.state))

                    {

                      memcpy(directions, successor.moves,  sizeof(successor.moves));

                       return  true;

                    }

               // 计算当前节点的评分，若小于限制，加入栈中，否则找超过的最小值

                    successor.score = score(successor.state, successor.depth);

               if(successor.score < depth_limit)

                      open.push(successor);

                     else

                    {

                       if (successor.score < min_depth)

                        min_depth = successor.score;

                    }

            }                   

          }

   }

    return  false;

 }

        

  void solve_puzzle(vector < int> tiles)

 {

    // 这里给出了BFS,DFS,A*和IDA*一共四种方法

    int moves[STEPSBOUND];

    //  深度优先搜索。

    //  solve_puzzle_by_depth_first_search(tiles, moves);

    //  宽度优先搜索。

    //  solve_puzzle_by_breadth_first_search(tiles, moves);

    //  A* 搜索。解长度在 30 - 50 步之间的局面平均需要 7 s。UVa RT 1.004 s。

    //  solve_puzzle_by_a_star(tiles, moves);

    //  IDA* 搜索。解长度在 30 - 50 步之间的局面平均需要 1.5 s。UVa RT 0.320 s。

   solve_puzzle_by_iterative_deepening_a_star(tiles, moves);

    //  输出走法步骤。

    for ( int i =  0; i < STEPSBOUND; i++)

   {

      // 有一种情况是初始状态本身就是目标状态，这种情况下，我们利用MOVE_NONE来标识

      if (moves[i] == MOVE_NONE)

             break;

           switch (moves[i])

          {

             case MOVE_LEFT:

              cout <<  " L ";

               break;

             case MOVE_RIGHT:

              cout <<  " R ";

                break;

             case MOVE_UP:

              cout <<  " U ";

                break;

             case MOVE_DOWN:

              cout <<  " D ";

                     break;

     }

   }

   cout << endl;

 }

        

  // 预先计算曼哈顿距离填表(曼哈顿距离为两者的横坐标之差的绝对值与纵坐标之差的绝对值之和)

  void cal_manhattan( void)

 {

    for ( int i =  0; i < SQUARES * SQUARES; i++)

      for ( int j =  0; j < SQUARES * SQUARES; j++)

          {

             int tmp =  0;

            tmp += (absi(i / SQUARES - j / SQUARES) + absi(i % SQUARES - j % SQUARES));

            manhattan[i][j] = tmp;

          }     

 }

        

  int main( int ac,  char *av[])

 {     

    // 计算曼哈顿距离，填表。

   cal_manhattan();

    int n, tile;

    // 利用vector容器装填一个完整的局面

   vector < int> tiles;

    // 读入样例       

   cin >> n;

    while (n--)

   {

      // 读入局面状态

     tiles.clear();

      for ( int i =  0; i < SQUARES * SQUARES; i++)

          {

            cin>>tile;

       tiles.push_back(tile);

          }

      // 判断是否有解，无解则输出相应信息，有解则使用相应算法解题

           if(solvable(tiles))

       solve_puzzle(tiles);

           else

            cout <<  " This puzzle is not solvable. " << endl;

   }

    return  0;

}