最长公共子序列

最长公共子序列

本文从三个层次分析最大公共子序列

1. 最大公共子序列长度
2. 最大公共子序列
3. 算法分析

 

首先来个区别：单词"cnblogs"

• 子序列：从单词中抽取字符，不能保证连续抽取。如”cn"、“cns"、”bgs"
• 连续子序列：从单词中连续抽取字符。如“bolog"、”cnbl"

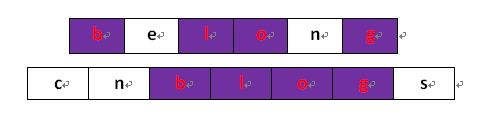
最长公共子序列（LCS：Longest Common Subsequence）顾名思义，就是几个词语中最长的相同子序列。比如“cnblogs"和”belong"最大公共子序列是“blog"

        

最长公共子序列是个非常有用的算法，可以判断两段文字间的”雷同程度“，从而可以判别抄袭。下面先介绍几种找出最长公共子序列长度的算法：

最大公共子序列长度

1.暴力算法

对于含有n个字符一个句子，每个位置有两种可能（出现 or 不出现），因此总共有2*2*2....总共2^n-1个（排除空序列）序列。这样找出来知道，在和另一个句子中的子序列意义比较（为了少算点可以只比角长度相同的）。

显然，这种方法也太暴力了，指数增长，一点技术含量没有。直接舍去了。

2.递归算法

把一个大问题看成几个已经解决了的子问题的综合。
        

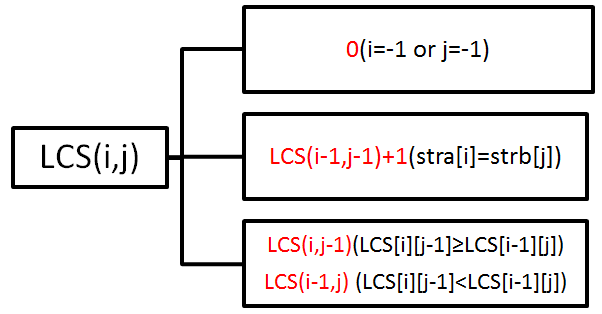
两个字符串，分别是stra和strb。如果对应长度是lena和lenb。那么就是求解LCS(lena, lenb)。此时先比较stra[lena-1]和strb[lenb-1](字符串是从0开始计数的)。

• 如果相同则等于LCS(lena-1,lenb-1)+1,此时LCS(lena-1,lenb-1)不知道，接着递归
• 如果不同则比较LCS(lena-2,lenb-1)和LCS(lena-1,lenb-2)，前者大，就等于前者；后者大，后者。中间步骤不知道，接着递归
• 如果递归到了LCS()中的一个数为-1了那就相当于存在空串了，公共的长度肯定是0了。

参考程序:

#include <stdio.h>
#include <string.h>
int LCS(int m, int n);
char a[100];
char b[100];

int main()
{
    strcpy(a, "cnblogs");
    strcpy(b, "belong");
    int lena = strlen(a);
    int lenb = strlen(b);
    printf("LCS:%d\n", LCS(lena-1, lenb-1));
    return 0;
}

int LCS(int m, int n)
{
    if(m==-1 || n==-1)
        return 0;
    else if(a[m] == b[n])
        return 1 + LCS(m-1, n-1);
    else
        return LCS(m-1, n) > LCS(m, n-1) ? LCS(m-1, n):LCS(m, n-1);
}

3.动态规划

和递归算法的大化小问题思路不同，动态规划是把一个问题转化成一些列的单阶段问题。

在利用动态规划找出最长公共子序列时，目标是求LCR(lena,lenb)，我们把任意两点的LCR求出来，此时要用二位数组表示。

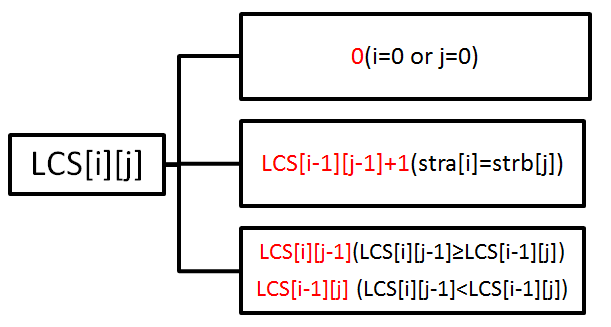
基本原理公式还是那样：

此时注意，字符串计数是从0开始的，现在用二维数组表示，就不能像上面一样出现-1了，现在用二维数组表示个数时，从1开始，即LCR[m][n]，表示stra[m-1]和strb[n-1]之间的最大子序列长度。

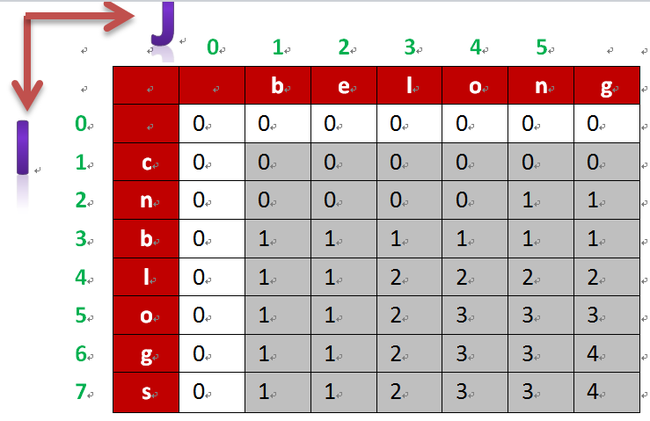
现在用具体的例子阐明动态规划的过程：

stra = "cnblogs"

strb = "belong"

• LCR[m][0]=0(表示：str[m-1] 和”空“间的关系)；同理LCR[0][n]=0
• LCR[1][1]:先看stra[0]和strb[0]间想不相同（'c'和‘b'不相同），就比较LCR[1][0] 和LCR[1][0]都为0，那么LCR[1][1]为0；
• 一直这样做下去......

         

参考程序：

#include <stdio.h>
#include <string.h>
char stra[100], strb[100];
int lena, lenb; 
int matrix[100][100];
void LCS();
int main()
{
    strcpy(stra, "cnblogs");
    strcpy(strb, "belong");
    lena = strlen(stra);
    lenb = strlen(strb);
    memset(matrix, 0, sizeof(matrix));
    LCS();
    return 0;
}

void  LCS()
{
    int i=0, j=0;
    for(i=0; i<lena; i++)
    {
        for(j=0; j<lenb; j++)
        {
            if(stra[i] == strb[j])
            {
                matrix[i+1][j+1] = matrix[i][j] + 1;
            }
            else
            {
                if(matrix[i+1][j] >= matrix[i][j+1])
                {
                    matrix[i+1][j+1] = matrix[i+1][j];
                }
                else
                {
                    matrix[i+1][j+1] = matrix[i][j+1];
                }
            }
        }
    }

    printf("LCS:%d\n", matrix[lena][lenb]);
}

最大公共子序列

有了最长公共子序列长度核心公式，求个长度还是很容易的，现在要求出具体的最大公共子序列。暴力算法是理论上是可以求出来的，但是过于繁琐与低效，弃了。动态规划与递归思路是一样的。

动态规划

这样标记：

• 当stra[i] == strb[j]时，标斜向上的箭头（记值为0）
• 当LCR[i+1][j]≥LCR[i][j+1]时，标向左箭头（记值为1）
• 当LCR[i+1][j]<LCR[i][j+1]时，标向上箭头（记值为-1）

寻找子序列:

• 见0记下， i--, j--
• 见1左拐，j--
• 见-1上拐，i--

图示说明：

      

参考算法：

#include <stdio.h>
#include <string.h>
char stra[100], strb[100];
int lena, lenb; 
int matrix[100][100];
int tag[100][100];
void LCS();
void getLCS();
int main()
{
    strcpy(stra, "cnblogs");
    strcpy(strb, "belong");
    lena = strlen(stra);
    lenb = strlen(strb);
    memset(matrix, 0, sizeof(matrix));
    LCS();
    getLCS();
    return 0;
}

void  LCS()
{
    int i=0, j=0;
    for(i=0; i<lena; i++)
    {
        for(j=0; j<lenb; j++)
        {
            if(stra[i] == strb[j])
            {
                matrix[i+1][j+1] = matrix[i][j] + 1;
                tag[i+1][j+1] = 0;
            }
            else
            {
                if(matrix[i+1][j] >= matrix[i][j+1])
                {
                    matrix[i+1][j+1] = matrix[i+1][j];
                    tag[i+1][j+1] = 1;
                }
                else
                {
                    matrix[i+1][j+1] = matrix[i][j+1];
                    tag[i+1][j+1] = -1;
                }
            }
        }
    }
    //输出次数矩阵
    for (i=1; i<=lena; i++)
    {
        for (j=1; j<=lenb; j++)
            printf("%d ", matrix[i][j]);
        printf("\n");
    }
    printf("****************\n");
    //输出方向转移矩阵
    for (i=1; i<=lena; i++)
    {
        for (j=1; j<=lenb; j++)
            printf("%d ", tag[i][j]);
        printf("\n");
    }
    printf("LCS:%d\n", matrix[lena][lenb]);
}

void getLCS()
{
    int i = lena, j = lenb, sum=0;
    char seq[100];
    while(i != 0 && j != 0)
    {
        if(tag[i][j] == 0)
        {
            seq[sum] = stra[i-1];
            i--;
            j--;
            sum++;
        }
        else if(tag[i][j] == 1)
            j--;
        else
            i--;
    }
    for(i=sum-1; i>=0; i--)
        printf("%c ", seq[i]);
}

递归算法

递归算法输出矩阵的思路与动态规划思路完全一致，就是在递归过程中标记，再回溯即可。

参考代码：

#include <stdio.h>
#include <string.h>
int LCS(int m, int n);
void getLCS();
char stra[100], strb[100];
int lena, lenb;
int tag[100][100];
char seq[100];
int main()
{
    int i, j;
    memset(tag, 0, sizeof(tag));
    strcpy(stra, "cnblogs");
    strcpy(strb, "belong");
    lena = strlen(stra);
    lenb = strlen(strb);
    printf("LCS:%d\n", LCS(lena-1, lenb-1));
    getLCS();
    for(i=0; i<=lena; i++)
    {
        for(j=0; j<=lenb; j++)
            printf("%d ", tag[i][j]);
        printf("\n");
    }

    return 0;
}

int LCS(int m, int n)
{
    if(m==-1 || n==-1)
    {
        return 0;
    }
    else if(stra[m] == strb[n])
    {
        tag[m+1][n+1] = 1;
        return 1 + LCS(m-1, n-1);
    }
    else
    {
        if(LCS(m, n-1) > LCS(m-1, n))
        {
            tag[m+1][n+1] = 2;
            return LCS(m, n-1);
        }
        else
        {
            tag[m+1][n+1] = 3;
            return LCS(m-1, n);
        }
    }
}

void getLCS()
{
    int i = lena, j = lenb, sum=0;
    while(i != 0 && j != 0)
    {
        if(tag[i][j] == 1)
        {
            seq[sum] = stra[i-1];
            i--;
            j--;
            sum++;
        }
        else if(tag[i][j] == 2)
            j--;
        else
            i--;
    }
    printf("The lCS is:");
    for(i=sum-1; i>=0; i--)
        printf("%c ", seq[i]);
    printf("\n");
}

算法分析

m表示第一个字串长度，n表示第二个字串长度。

动态规划

时间复杂度：

• 建立矩阵需要，需要花费时间o(mn)
• 回溯需要至多花费时间o(m+n)

综上，两者相加，时间复杂度为o(mn)

空间复杂度：

• 构建矩阵需要空间o(mn)
• 构建标记矩阵需要空间o(mn)

综上，二者相加，空间复杂度为o(mn)

 

 

 

 

 

 

分类:  算法&&程序设计