回溯法入门学习之二(九宫格与数独)
回溯法的基本做法是搜索解空间,一种组织得井井有条的,能避免不必要搜索的穷举式搜索法。上文“回溯法入门学习之一”
http://128kj.iteye.com/blog/1722216中已给出了一个框架:
"深度优先搜索+回溯"递归框架:
函数DFS(节点){
如果(节点=目标节点) {找到目标,跳出}
遍历所有下一层节点for(int i=0;i<k;i++){
标记下一层节点i已访问;
DFS(下一层的节点i)
恢复i为未访问
}
}
下面使用上面框架再解一例(数独问题):
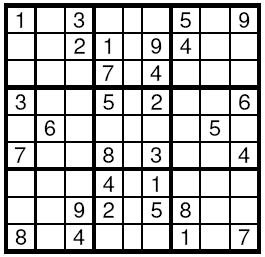
题目大意,如上图(一):
把一个9行9列的网格,再细分为9个3*3的子网格,要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字,即每行、每列、每个子网格内都不允许出现相同的数字。空格是待填位置,其他均为已填入的数字。
要求填完九宫格并输出(如果有多种结果,则只需输出其中一种),
如果给定的九宫格无法按要求填出来,则输出原来所输入的未填的九宫格。
如上图一中的9个子网络,我们假设子网格的序号如下编排图(二):
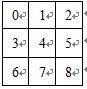
先讨论一下上图(一)中第i行j列的数字是属于哪个子网格的,
由于0<=i、j<=8,我们有图(三):
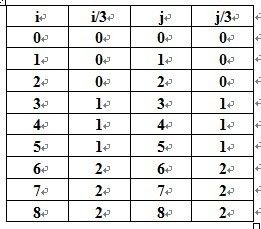
令a= i/3 , b= j/3 ,根据九宫格的行列与子网格(grid)的关系,我们有图(四):
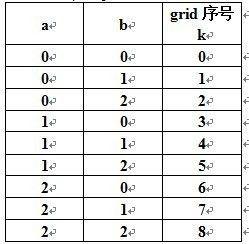
不难发现 3a+b=k,即 3*(i/3)+j/3=k。即图一中第i行j列的数字,属于第k个子网络
算法分析: DFS+回溯
1.把所有空格位置找出来,对他们进行dfs填补(用1,2,3,...9去试填)
2.剪枝方法(九宫格中已有数字的不用试填),把搜索过的相应位置搜索完复位
样例:
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
"深度优先搜索+回溯"递归框架:
函数DFS(节点){
如果(节点=目标节点) {找到目标,跳出}
遍历所有下一层节点for(int i=0;i<k;i++){
标记下一层节点i已访问;
DFS(下一层的节点i)
恢复i为未访问
}
}
下面使用上面框架再解一例(数独问题):

题目大意,如上图(一):
把一个9行9列的网格,再细分为9个3*3的子网格,要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字,即每行、每列、每个子网格内都不允许出现相同的数字。空格是待填位置,其他均为已填入的数字。
要求填完九宫格并输出(如果有多种结果,则只需输出其中一种),
如果给定的九宫格无法按要求填出来,则输出原来所输入的未填的九宫格。
如上图一中的9个子网络,我们假设子网格的序号如下编排图(二):

先讨论一下上图(一)中第i行j列的数字是属于哪个子网格的,
由于0<=i、j<=8,我们有图(三):

令a= i/3 , b= j/3 ,根据九宫格的行列与子网格(grid)的关系,我们有图(四):

不难发现 3a+b=k,即 3*(i/3)+j/3=k。即图一中第i行j列的数字,属于第k个子网络
算法分析: DFS+回溯
1.把所有空格位置找出来,对他们进行dfs填补(用1,2,3,...9去试填)
2.剪枝方法(九宫格中已有数字的不用试填),把搜索过的相应位置搜索完复位
样例:
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
import java.util.Scanner;
public class Main{
private int table[][];//用一个二维数组表示九宫格
private int pos[];//记录要填的空格位置
private int posNum;//要填的空格标号(从0开始)
private boolean rUsed[][];//rUsed[i][x] 标记在第i行中数字x是否出现了
private boolean cUsed[][];//cUsed[j][y] 标记在第j列中数字y是否出现了
private boolean sUsed[][];//sUsed[k][x] 标记在第k个3*3子格中数字z是否出现子
private boolean finish_dfs;//是否已找到了答案
public void go(){
Scanner in=new Scanner(System.in);
int cnt=in.nextInt();
while((cnt--)!=0){
//初始化数据
posNum = 0;
pos=new int[90];
table=new int[9][9];
rUsed=new boolean[9][10];
cUsed=new boolean[9][10];
sUsed=new boolean[9][10];
String line=null;
finish_dfs = false;
for(int i=0;i< 9;i++){ //准备输入数据
line=in.next();
for(int j=0;j< 9;j++){
table[i][j]=line.charAt(j)-'0';
if (table[i][j]!=0 ) {
rUsed[i][table[i][j]] = true;//table[i][j]这个数字在i行中已有了
cUsed[j][table[i][j]] = true;
int k = (i/3)*3+(j/3);
sUsed[k][table[i][j]] = true;//table[i][j]这个数字在第k个小网络中已有了
}
else {
pos[posNum++] = i*9+j;//记录要填的空格位置及标号
}
}
}
dfs_sudoku(0);
}
}
private void outre(){//输出结果
for ( int i = 0; i < 9; i++ ) {
for ( int j = 0; j < 9; j++ ) {
System.out.printf( "%d", table[i][j] );
}
System.out.println();
}
//System.out.println();
}
void dfs_sudoku( int n ){//深度优先搜索+回溯,试填第n个空格)
if ( n >= posNum ) {
finish_dfs = true;
outre();
return;
}
//根据要填的空格位置,计算空格的所在的行,列坐标及处在哪个小网络
int r = pos[n]/9;//空格的行坐标
int c = pos[n]%9;//空格的列坐标
int s = (r/3)*3+(c/3);//小网络的标号
for ( int i = 1; i <= 9 && !finish_dfs; i++ ) {//用1,2,3...9去试填)
if ( rUsed[r][i] ) continue;//第r行有i
if ( cUsed[c][i] ) continue;//第c列有i
if ( sUsed[s][i] ) continue;//第k个小网络有i
rUsed[r][i] = cUsed[c][i] = sUsed[s][i] = true;
table[r][c] = i;//第r行c列试填数字i
dfs_sudoku( n+1 );//递归试填第n+1个空格,成功或失败,如果成功则输出,失败则回溯
table[r][c] = 0;//回溯
rUsed[r][i] = cUsed[c][i] = sUsed[s][i] = false;
}
return;
}
public static void main(String[] args){
Main ma=new Main();
ma.go();
}
}