1. Brute-force substring search
-- Check for pattern starting at each text position.
-- Java Implementation
public static int search(String pat, String txt)
{
int M = pat.length();
int N = txt.length();
for (int i = 0; i <= N - M; i++)
{
int j;
for (j = 0; j < M; j++)
if (txt.charAt(i+j) != pat.charAt(j))
break;
if (j == M) return i;
}
return N;
}
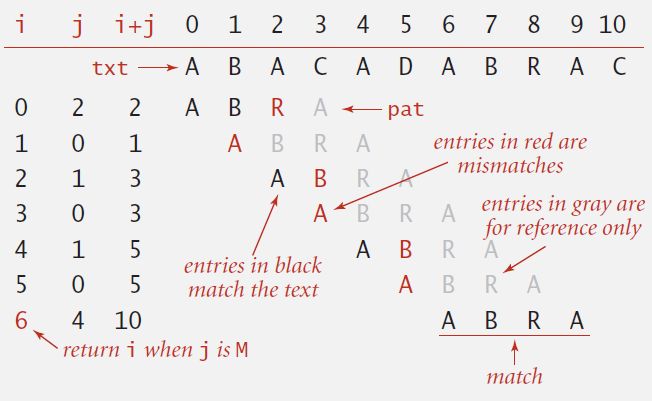
-- Brute-force algorithm can be slow if text and pattern are repetitive: ~ M N char compares.

-- Same sequence of char compares as previous implementation.
- i points to end of sequence of already-matched chars in text.
- j stores # of already-matched chars (end of sequence in pattern).
- Java Implementation
public static int search(String pat, String txt)
{
int i, N = txt.length();
int j, M = pat.length();
for (i = 0, j = 0; i < N && j < M; i++)
{
if (txt.charAt(i) == pat.charAt(j)) j++;
else { i -= j; j = 0; } // explicit backup, we can add if(i >= N-M) break;
}
if (j == M) return i - M;
else return N;
}
-- In many applications, we want to avoid backup in text stream. Brute-force algorithm needs backup for every mismatch.
2. Knuth-Morris-Pratt substring search
-- DFA is abstract string-searching machine.
- Finite number of states (including start and halt).
- Exactly one transition for each char in alphabet.
- Accept if sequence of transitions leads to halt state.

-- State = number of characters in pattern that have been matched = length of longest prefix of pat[] that is a suffix of txt[0..i]
-- Java Implementation:
public int search(String txt)
{
int i, j, N = txt.length();
for (i = 0, j = 0; i < N && j < M; i++)
j = dfa[txt.charAt(i)][j];
if (j == M) return i - M;
else return N;
}
-- Key differences from brute-force implementation.
- Need to precompute dfa[][] from pattern.
- Text pointer i never decrements.
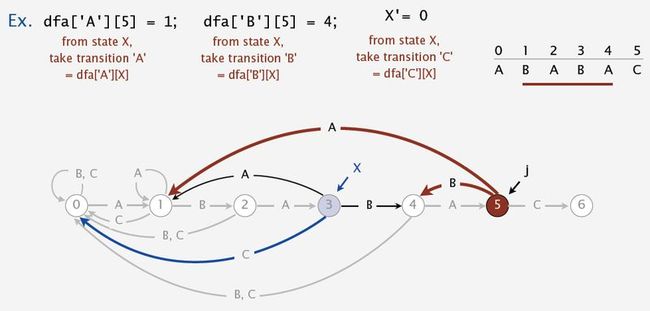
-- Build DFA from pattern:
- Match transition: If in state j and next char c == pat.charAt(j), go to j+1.
- Mismatch transition: If in state j and next char c != pat.charAt(j), then the last j-1 characters of input are pat[1..j-1], followed by c. To compute dfa[c][j]: Simulate pat[1..j-1] on DFA and take transition c.
- Takes only constant time if we maintain state X which is the state resulting from simulating pat[1...j-1] on DFA.
For each state j:
a) Copy dfa[][X] to dfa[][j] for mismatch case.
b) Set dfa[pat.charAt(j)][j] to j+1 for match case.
c) Update X.
- Java Implementation:
public KMP(String pat)
{
this.pat = pat;
M = pat.length();
dfa = new int[R][M];
dfa[pat.charAt(0)][0] = 1;
for (int X = 0, j = 1; j < M; j++)
{
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][X];
dfa[pat.charAt(j)][j] = j+1;
X = dfa[pat.charAt(j)][X];
}
}
- Running time: M character accesses (but space and time proportional to R M).
3. Boyer-Moore Substring Search
-- Scan characters in pattern from right to left.
-- Can skip as many as M text chars when finding one not in the pattern.
- Mismatch character not in pattern : increment i one character beyond the mismatched character
- Mismatch character in pattern: align rightmost character in the pattern with the mismatched character without backup
- Mismatch character in pattern: increment i by 1. ( if alignment need backup)
-- Precompute index of rightmost occurrence of character c in pattern (-1 if character not in pattern).
right = new int[R];
for (int c = 0; c < R; c++)
right[c] = -1;
for (int j = 0; j < M; j++)
right[pat.charAt(j)] = j;
public int search(String txt)
{
int N = txt.length();
int M = pat.length();
int skip;
for (int i = 0; i <= N-M; i += skip)
{
skip = 0;
for (int j = M-1; j >= 0; j--)
{
if (pat.charAt(j) != txt.charAt(i+j))
{
skip = Math.max(1, j - right[txt.charAt(i+j)]);
break;
}
}
if (skip == 0) return i;
}
return N;
}
-- Substring search with the Boyer-Moore mismatched character heuristic takes about ~ N / M character compares to search for a pattern of length M in a text of length N.
-- Can be as bad as ~ M N.
4. Rabin-Karp fingerprint search
-- Algorithm
-- Compute a hash of pattern characters 0 to M - 1.
-- For each i, compute a hash of text characters i to M + i - 1.
-- If pattern hash = text substring hash, check for a match.
-- Modular hash function. Using the notation ti for txt.charAt(i), compute :
xi = ti R^M-1 + ti+1 R^M-2 + … + ti+M-1 R^0 (mod Q)
-- Horner's method. Linear-time method to evaluate degree-M polynomial:
// Compute hash for M-digit key
private long hash(String key, int M)
{
long h = 0;
for (int j = 0; j < M; j++)
h = (R * h + key.charAt(j)) % Q;
return h;
}

-- How to efficiently compute xi+1 given that we know xi:
xi+1 = ( xi – t i R^M–1 ) R + t i +M
public class RabinKarp
{
private long patHash; // pattern hash value
private int M; // pattern length
private long Q; // modulus
private int R; // radix
private long RM; // R^(M-1) % Q
public RabinKarp(String pat) {
M = pat.length();
R = 256;
Q = longRandomPrime(); //a large prime (but avoid overflow)
RM = 1; //precompute R^(M – 1) (mod Q)
for (int i = 1; i <= M-1; i++)
RM = (R * RM) % Q;
patHash = hash(pat, M);
}
private long hash(String key, int M)
{ /* as before */ }
public int search(String txt)
{
int N = txt.length();
int txtHash = hash(txt, M);
if (patHash == txtHash) return 0;
for (int i = M; i < N; i++)
{
txtHash = (txtHash + Q - RM*txt.charAt(i-M) % Q) % Q;
txtHash = (txtHash*R + txt.charAt(i)) % Q;
if (patHash == txtHash) return i - M + 1;
}
return N;
}
}
-- Two versions of Implementation:
- Monte Carlo version: Return match if hash match.
- Las Vegas version: Check for substring match if hash match; continue search if false collision.
-- Advantages:
- Extends to 2d patterns.
- Extends to finding multiple patterns.
-- Disadvantages.
- Arithmetic ops slower than char compares.
- Las Vegas version requires backup.
- Poor worst-case guarantee.
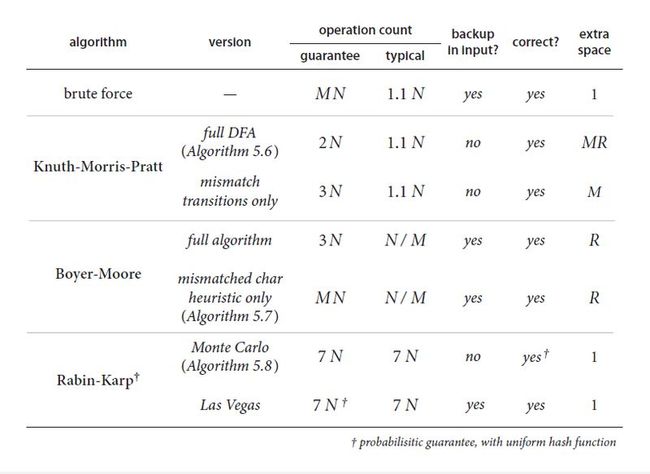
5. Substring search cost summary