求n个元素集合的子集(幂集)或n个元素的组合

回溯法是设计递归过程的一种重要方法,它的求解过程是遍历一个状态树,只是这颗树不是预先建立的而是隐含的遍历过程,在遍历过程中对各个元素进行取舍。
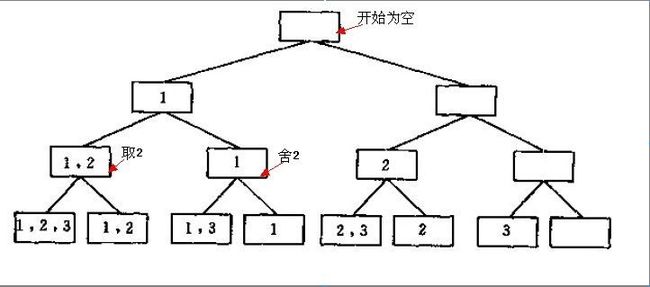
如求n个元素集合的子集，如A = {1, 2, 3}则A集合的子集有:
  PrA = {{1,2,3}, {1,2}, {1,3},{1},{2,3},{2},{3},{}}

遍历过程中的状态树:

#include <iostream>
#include <stack>
using namespace std;

const int _N = 1000;
int list[_N];
int n;

void dfs(int i, int n, stack<int> s)
{
	if(i == n)
	{
		cout<<"{";
		while(!s.empty())
		{
			cout<<" "<<s.top();
			s.pop();
		}
		cout<<"}"<<endl;
	}else
	{
		s.push(list[i]); //取
		dfs(i + 1, n, s);
		s.pop(); //舍
		dfs(i + 1, n, s);
	}
}
int main()
{
	int i;
	while(cin>>n)
	{
		stack<int> s;
		for(i = 0; i < n; i++)
			list[i] = i + 1; //初始化
		dfs(0, n, s);
	}
	return 0;
}