连续子数组最大和和最长递增子序列
本文内容框架:
§1 连续子数组最大和
基本方法、分治策略求解、动态规划求解
§2 最长递增子序列
排序+LCS求解、动态规划、动态规划+二分查找
§3 小结
§1 连续子数组最大和
连续子数组最大和
连续子数组最大和,又叫最大子序列和或最大数组和,不过这里的序列好像有点不是很妥。
1.1问题描述
一个有N个元素的整型数组arr,有正有负,数组中连续一个或多个元素组成一个子数组,这个数组当然有很多子数组,求子数组之和的最大值。
1.2基本方法
枚举所有可能子数组,直接实现的时间复杂度是O(n³),代码如下:
╔
int MaxSubsequenceSum( const int A[ ], int N )
{
int ThisSum, MaxSum, i, j, k;
MaxSum = 0;
for( i = 0; i < N; i++ )
for( j = i; j < N; j++ )
{
ThisSum = 0;
for( k = i; k <= j; k++ )
ThisSum += A[ k ];
if( ThisSum > MaxSum )
MaxSum = ThisSum;
}
return MaxSum;
}
做一点小优化:没有必要每次都去从头计算ThisSum,可以之间在前面的基础上加上增加的那一个,时间复杂度为O(n²),还看代码:
1.3分治策略求解
分治策略的时间复杂度是O(NlogN)。分治策略在这里是从中间向两边延伸最大子数组求最大和。
static int Max3( int A, int B, int C )
{
return A > B ? A > C ? A : C : B > C ? B : C;
}
static int MaxSubSum( const int A[ ], int Left, int Right )
{
int MaxLeftSum, MaxRightSum;
int MaxLeftBorderSum, MaxRightBorderSum;
int LeftBorderSum, RightBorderSum;
int Center, i;
if( Left == Right ) /* Base case */
if( A[ Left ] > 0 )
return A[ Left ];
else
return 0;
Center = ( Left + Right ) / 2;
MaxLeftSum = MaxSubSum( A, Left, Center );
MaxRightSum = MaxSubSum( A, Center + 1, Right );
MaxLeftBorderSum = 0; LeftBorderSum = 0;
for( i = Center; i >= Left; i-- )
{
LeftBorderSum += A[ i ];
if( LeftBorderSum > MaxLeftBorderSum )
MaxLeftBorderSum = LeftBorderSum;
}
MaxRightBorderSum = 0; RightBorderSum = 0;
for( i = Center + 1; i <= Right; i++ )
{
RightBorderSum += A[ i ];
if( RightBorderSum > MaxRightBorderSum )
MaxRightBorderSum = RightBorderSum;
}
return Max3( MaxLeftSum, MaxRightSum,
MaxLeftBorderSum + MaxRightBorderSum );
}
int MaxSubsequenceSum( const int A[ ], int N )
{
return MaxSubSum( A, 0, N - 1 );
}
1.4动态规划求解
╔
设b[i]表示以a[i]结尾 的子数组的最大子段和,即:b[i]=max{sum(a[j~k])},其中0<=j<=i,j<=k<=i。因此对于数组a[0~n]的最大字段和为max{b[i]},其中0<=i<n。
在计算b[i]时,可以考虑以下三种情况:
1,b[i] = b[i-1]+a[i],当b[i-1]>0时,这时候的b[i]中包含a[i]。
2,b[i] = a[i],当b[i-1]<=0,这时候以a[i]重新作为b[i]的起点。
3,b[i]不包含a[i]的情况,这种情况在计算b[i]之前已经计算处结果,保存在b[0~i-1]中。最后计算max{b[i]}时会考虑到。
b[i] = max{ b[i-1]+a[i],a[i]}。
而数组a[0~n]则为max{b[i]}。在实现时,可以省略数组b[i]。
╝②
动态规划求解的时间复杂度是O(n)。可以记录最大连续子数组和的起始和末尾位置。
int MaxSubsequenceSum( const int A[ ], int N )
{
int ThisSum, MaxSum, j;
ThisSum = MaxSum = 0;
for( j = 0; j < N; j++ )
{
ThisSum += A[ j ];
if( ThisSum > MaxSum )
MaxSum = ThisSum;
else if( ThisSum < 0 )
ThisSum = 0;
}
return MaxSum;
}
╝①
1.5问题拓展——最大子矩阵和
对于最大子矩阵和,当然可以使用枚举方法,但是这显然不是作者想要的,一维的情况已经得到很好的解法,要是能将二维情况转换为一维的情况,效率就容易接受了。
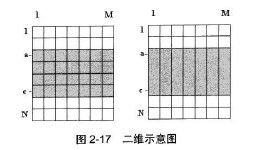
最大子矩阵和的行也是连续的,计算第 i 行和第 j 行之间的最大子矩阵,可以将 i 行和 i 行之间的同一列的元素纵向相加,这样子矩阵就转换为一维的数组,就是下图所示:
╔
固定第i列到第j列的范围,寻找在这个范围内的最大子矩阵,这个寻找过程,把每行第i列上的元素到第j列的元素分别求和,就转变为了一维的情况。由于有C(n,2)种列的组合,而求一维的子序列需要n的时间,所以,总体上时间复杂度为O(n^3)。
仍旧贴代码:
#include <iostream>
using namespace std;
#define N 4
int main() {
int A[N][N] = { 0, -2, -7, 0, 9, 2, -6, 2, -4, 1, -4, 1, -1, 8, 0, -2 };
int F[N+1][N+1];
int P[N+1];
int Q[N+1];
int max, index_i, index_j;
// F
for(int i=1; i<N+1; i++) {
F[i][0] = 0; // 第0列,即哨兵列
F[i][1] = A[i-1][0]; // 第1列
}
for(int i=1; i<N+1; i++) {
for(int j=2; j<N+1; j++) { // 从第2列开始
F[i][j] = F[i][j-1] + A[i-1][j-1];
}
}
// P,Q
max = INT_MIN;
for(int i=1; i<N+1; i++) {
for(int j=i+1; j<N+1; j++) {
P[1] = F[1][j]-F[1][i-1];
Q[1] = P[1];
for(int k=2; k<N+1; k++) {
P[k] = P[k-1]>0?(P[k-1]+F[k][j]-F[k][i-1]):(F[k][j]-F[k][i-1]);
Q[k] = Q[k-1]>P[k]?Q[k-1]:P[k];
}
if(Q[N] > max) {
max = Q[N];
index_i = i;
index_j = j;
}
}
}
// max
cout << max << endl;
cout << index_i << " , " << index_j << endl;
system("PAUSE");
return 0;
}
╝③
§2 最长递增子序列
最长递增子序列
2.1问题描述
设L=<a1,a2,…,an>是n个不同的实数的序列,L的递增子序列是这样一个子序列Lin=<aK1,ak2,…,akm>,其中k1<k2<…<km且aK1<ak2<…<akm。求最大的m值。
╔
2.2动态规划求解
从后向前分析,如果a[i]大于前面所有的数,则dp[i]在max{dp[j],j<i}的基础上加1(dp[i]表示数组a[i-1]为末尾的最长递增子序列的长度)。
╔
设dp(i)表示L中以ai为末元素的最长递增子序列的长度。则有如下的递推方程:
这个递推方程的意思是,在求以ai为末元素的最长递增子序列时,找到所有序号在L前面且小于ai的元素aj,即j<i且aj<ai。如果这样的元素存在,那么对所有aj,都有一个以aj为末元素的最长递增子序列的长度dp(j),把其中最大的dp(j)选出来,那么f(i)就等于最大的f(j)加上1,即以ai为末元素的最长递增子序列,等于以使f(j)最大的那个aj为末元素的递增子序列最末再加上ai;如果这样的元素不存在,那么ai自身构成一个长度为1的以ai为末元素的递增子序列。
╝④
#include <iostream>
using namespace std;
/* 最长递增子序列 LIS
* 设数组长度不超过 30
* DP
*/
int dp[31]; /* dp[i]记录到[0,i]数组的LIS */
int lis; /* LIS 长度 */
int LIS(int * arr, int size)
{
for(int i = 0; i < size; ++i)
{
dp[i] = 1;
for(int j = 0; j < i; ++j)
{
if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
{
dp[i] = dp[j] + 1;
if(dp[i] > lis)
{
lis = dp[i];
}
}
}
}
return lis;
}
/* 输出LIS */
void outputLIS(int * arr, int index)
{
bool isLIS = 0;
if(index < 0 || lis == 0)
{
return;
}
if(dp[index] == lis)
{
--lis;
isLIS = 1;
}
outputLIS(arr,--index);
if(isLIS)
{
printf("%d ",arr[index+1]);
}
}
void main()
{
int arr[] = {1,-1,2,-3,4,-5,6,-7};
/* 输出LIS长度; sizeof 计算数组长度 */
printf("%d\n",LIS(arr,sizeof(arr)/sizeof(int)));
/* 输出LIS */
outputLIS(arr,sizeof(arr)/sizeof(int) - 1);
printf("\n");
}
2.3排序+LCS求解
这个方法也是很直观的,对原数组a进行排序得到一个有序的数组b, 这样出现在数组a的最长递增子序列也一定是数组b的子序列。
#include <iostream>
using namespace std;
/* 最长递增子序列 LIS
* 设数组长度不超过 30
* quicksort + LCS
*/
void swap(int * arr, int i, int j)
{
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void qsort(int * arr, int left, int right)
{
if(left >= right) return ;
int index = left;
for(int i = left+1; i <= right; ++i)
{
if(arr[i] < arr[left])
{
swap(arr,++index,i);
}
}
swap(arr,index,left);
qsort(arr,left,index-1);
qsort(arr,index+1,right);
}
int dp[31][31];
int LCS(int * arr, int * arrcopy, int len)
{
for(int i = 1; i <= len; ++i)
{
for(int j = 1; j <= len; ++j)
{
if(arr[i-1] == arrcopy[j-1])
{
dp[i][j] = dp[i-1][j-1] + 1;
}else if(dp[i-1][j] > dp[i][j-1])
{
dp[i][j] = dp[i-1][j];
}else
{
dp[i][j] = dp[i][j-1];
}
}
}
return dp[len][len];
}
void main()
{
int arr[] = {1,-1,2,-3,4,-5,6,-7};
int arrcopy [sizeof(arr)/sizeof(int)];
memcpy(arrcopy,arr,sizeof(arr));
qsort(arrcopy,0,sizeof(arr)/sizeof(int)-1);
/* 计算LCS,即LIS长度 */
int len = sizeof(arr)/sizeof(int);
printf("%d\n",LCS(arr,arrcopy,len));
}
2.4动态规划+二分查找
如果对前面的方法的时间复杂度(前两种复杂度是O(n²)还不满意的,这里就有救了,动态规划+二分查找的实现时间复杂度是O(NlogN)。
在前i个元素中的所有长度为len的递增子序列中找到这样一个序列,它的最大元素比arr[i+1]小,而且长度要尽量的长,如此,只需记录len长度的递增子序列中最大元素的最小值就能使得将来的递增子序列尽量地长。
方法:维护一个数组B[i],记录长度为i的递增子序列中最大元素的最小值,并对于数组中的每个元素考察其是哪个子序列的最大元素,二分更新B数组,最终i的值便是最长递增子序列的长度。这个方法真是太巧妙了,妙不可言。
╝⑥
╔
int LIS(int d[], int n){
int *B = new int[n];
int left, right, mid, len = 1;
B[0] = d[1]; //为了和上面的一致,我们从1开始计数吧:)
for(i = 2; i <= n; ++i){
left = 0, right = len;
while(left <= right){
mid = (left + right) / 2;
if(B[mid] < d[i]) left = mid + 1; //二分查找d[i]的插入位置
else right = mid - 1;
}
B[left] = d[i]; //插入
if(left > len) len++; //d[i]比现有的所有数字都大,所以left 才会大于 len。
}
delete[] B;
return len;
}
╝⑤
§3 小结
这篇博文介绍了最大连续子数组和最长递增子序列的求解,两个问题都介绍了数种方法,希望能彻底理解问题的本质以及求解方法。如果你有任何建议或者批评和补充,请不吝留言指出,不胜感激,更多参考请移步互联网。
参考:
①shengjin: http://www.cnblogs.com/shengjin/archive/2010/01/08/1641975.html
②clearriver: http://blog.csdn.net/clearriver/article/details/4224154
③xiaodongrush: http://www.cnblogs.com/pangxiaodong/archive/2011/09/02/2163445.html
④算法驿站: http://blog.pfan.cn/rickone/13086.html
⑤felix021: http://www.felix021.com/blog/read.php?1587
⑥勇幸|Thinking: http://www.ahathinking.com/archives/117.html