1. The Vertex Cover Problem
-- Input: An undirected graph G = (V , E).
-- Goal: Compute a minimum-cardinality vertex cover -- a subset S subset of V that contains at least one endpoint of each edge of G.
-- The minimum size of a vertex cover of a star graph with n verities and a clique with n vertices is 1 and n-1 respectively
-- Suppose: Given a positive integer k as input, we want to check whether or not there is a vertex cover with size <= k. Could try all possibilities, would take C(n , k) = O(n^k ) time when k is small.
2. Substructure Lemma
-- Consider graph G, edge (u , v) in G, integer k >= 1. Let Gu = G with u and its incident edges deleted (similarly, Gv ). Then G
has a vertex cover of size k <=> Gu or Gv (or both) has a vertex cover of size (k - 1)
-- Proof:
<== Suppose Gu (say) has a vertex cover S of size k - 1. Write E = Eu (edges inside Gu) U Fu (edges incident to u). Since S has an endpoint of each edge of Eu, S U {u} is a vertex cover (of size k) of G.
==> Let S = a vertex cover of G of size k. Since (u , v) an edge of G, at least one of u , v (say u) is in S. Since no edges of Eu incident on u, S - {u} must be a vertex cover (of size k - 1) of Gu.
3. A Search Algorithm [Given undirected graph G = (V , E), integer k]
-- Pick an arbitrary edge (u , v) in E.
-- Recursively search for a vertex cover S of size (k - 1) in Gu.(G with u + its incident edges deleted). If found, return S U {u}.
-- Recursively search for a vertex cover S of size (k - 1) in Gv. If found, return S U {v}.
-- FAIL. [G has no vertex cover with size k]
4. Analysis of Search Algorithm
-- Correctness: Straightforward induction, using the substructure lemma to justify the inductive step.
-- Running time: Total number of recursive calls is O(2^k ) [branching factor <= 2, recursion depth <= k] (formally, proof by induction on k)
-- Also, O(m) work per recursive call (not counting work done by recursive subcalls)
-- Running time = O(m2^k) ==> Polynomial-time as long as k = O(log n) ==> better way than O(n^k)
5. The Traveling Salesman Problem
-- Input: A complete undirected graph with nonnegative edge costs.
-- Output: A minimum-cost tour (i.e., a cycle that visits every vertex exactly once).
-- Brute-force search: Takes about n! time
6. Hints from Bellman-Ford algorithm:
-- Proposed subproblems: For every edge budget i in {0, 1, . . . , n}, destination j in {1, 2, . . . . n}, let Lij = length of a shortest path from 1 to j that uses at most i edges. ==> can use less than i edges, solving all subproblems doesn't solve original problem.
-- Proposed subproblems: For every edge budget i in {0, 1, . . . , n}, destination j in {1, 2, . . . . n}, let Lij = length of a shortest path from 1 to j that uses exactly i edges. ==> can visit repeated vertex, solving all subproblems doesn't solve original problem.
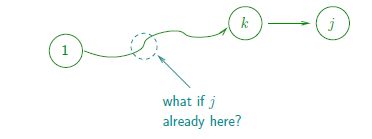
-- Proposed subproblems: For every edge budget i in {0, 1, . . . , n}, destination j in {1, 2, . . . . n}, let Lij = length of a shortest path from 1 to j that uses exactly i edges and visit no repeated vertices. Hope : Lij = min(k<>1,j){ Li-1,k + ckj}
-- Problem: What if j already appears on the shortest 1 --> k path with (i - 1) edges and no repeated vertices? ==> Concatenating 1-->k and k-->j yields a second visit to j (not allowed)
-- Upshot: To enforce constraint that each vertex visited exactly once, need to remember the identities of vertices visited in subproblem. [But not the order in which they're visited]
7. The Subproblems
-- For every destination j in {1, 2, ... , n}, every S subset of {1, 2, ... , n} that contains 1 and j , let L(S,j) = minimum length of a path from 1 to j that visits precisely the vertices of S [exactly once each]
-- Let P be a shortest path from 1 to j that visits the vertices S (assume |S| >= 2) [exactly once each]. If last hop of P is (k , j ), then P' is a shortest path from 1 to k that visits every vertex of S - {j} exactly once.
-- Corresponding recurrence: L(S,j) = min(k in S,k<>j){L(S-{j} , k) + ckj} ["size" of subproblem = |S|]
8. A Dynamic Programming Algorithm
-- Let A = 2-D array, indexed by subsets S subset of {1, 2, ... , n} that contain 1 and destinations j in {1, 2, ... , n}
-- Base case: A[S , 1] = 0 if S = {1} ; +Infinity otherwise [no way to avoid visiting vertex 1 twice]
-- For m = 2, 3, ... , n [m = subproblem size]
For each set S in {1, 2, ... , n} of size m that contains 1
For each j in S, j <> 1
A[S , j ] = min(k in S, k<>j){A[S - {j} , k] + ckj} [same as recurrence]
-- Return min(j=2,...,n) { A[{1, 2, ... , n} , j ] + cj1 } [ min cost from 1 to j visiting everybody once + cost of final hop of tour]
-- Running time: O( n 2^n ) O(n) = O(n^2 2^n)
-- O(n 2^n) : choices of j * choices of S = # of subproblems
-- O(n) : work per subproblem