When I came to topological order again in this online course (https://class.coursera.org/algs4partII-002) , I was told that it can be calculated as "Reverse Post-Order". What I came up first when I see this term, I was curious why the tutor didn't use "Pre-Order"?
Later , I realized that my understanding of "Post-Order" and "Pre-Order" was still against the root of a tree. It should be true that "Reverse Post-Order" is same as "Pre-Order" in terms of traversing from a root of a tree. (Correct me , if I'm wrong)
However for a DAG , "Reverse Post-Order" is not same as "Pre-order" if you traverse from any vertex (same for tree). For example, for the following DAG :
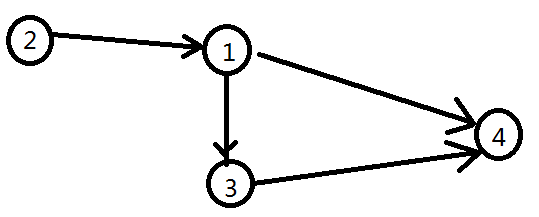
If we traverse from vertex 1, then the pre-order is : 1 , 3, 4, 2 (or 1, 4, 3, 2). Obviously it's not topological order. And the post-order is : 4, 3, 1, 2 and the reverse post-order is topological order.
Another thing is against the 2 DFS algorithm that calculates the SCC (Strongly Connected Components). The first DFS need to caculate the reverse post-order (not topological order, because the graph is not necessarily a DAG) on the reverse Graph and the second DFS is to traverse in the original graph in order of the first DFS output.
So the natural thought is why can't we calculate a post-order on the original graph in the first DFS phase ?
So let's look at the following example 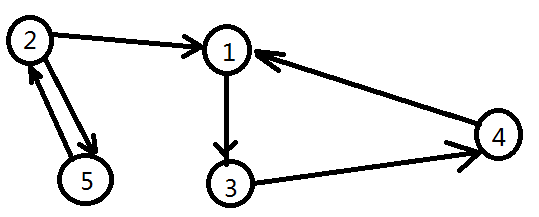
Obviously there are two SCCs {2,5} and {1, 3, 4}. Let's think from the second round DFS, if we traverse from 2 or 5, we will traverse all the graph and get only 1 SCC. That's not what we want. So in the first found of DFS, we should make sure any of {1,3,4} shoud before both 2 and 5 in the output. However if we output a post-order by DFS tranversing from 2, we may get 5 , 4, 3, 2, 1, which is not what we want.
O.K. now let's analyze this algorithm in general. In the second round of DFS, we want to traverse in post-order of it's meta graph (merging all the vertices in one SCC into one vertex). Using the above example, the meta graph is :
{2, 5} --> {1,3,4}
Let's call {2, 5} is a meta vertex A and {1,3,4} a meta vertex B. So we got :
A-->B
So for the first round of DFS, we can't use post-order, because post-order will output a vertex iff all it's children has already been visited, in that case we may out put any vertex in any SCC first. (i.e. vertex 5 in the above example)
How to resove it ? reverse it ! , if there is a path from meta vertex A to B , but no path from B to A, after reversing, there is a path from B to A but no path from A to B:
B<--A
So in the post-order of reverse graph, if we start from a vertex in B (before we traverse any vertex of A), then all vertices in B will appear before A and if we start from a vertex from A(before we traverse any vertex of B) then this vertex (the starting vertex) is before B.
注,由于原教程全为英文,所以为了避免某些关键term翻译不准确,索性全文用E文撰写,全文原创,谢谢:)