1. Reduction: Problem X reduces to problem Y if you can use an algorithm that solves Y to help solve X.
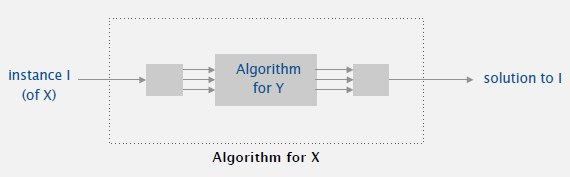
-- Cost of solving X = total cost of solving Y + cost of reduction.
2. Example of reduction: To solve element distinctness on N items:
-- Sort N items.
-- Check adjacent pairs for equality.
-- Cost of solving element distinctness. N log N + N .
3. Usage of Reduction : design algorithms. Since I know how to solve Y, can I use that algorithm to solve X ?
4. Convex hull reduces to sorting:
-- Choose point p with smallest (or largest) y-coordinate.
-- Sort points by polar angle with p to get simple polygon.
-- Consider points in order, and discard those that would create a clockwise turn.
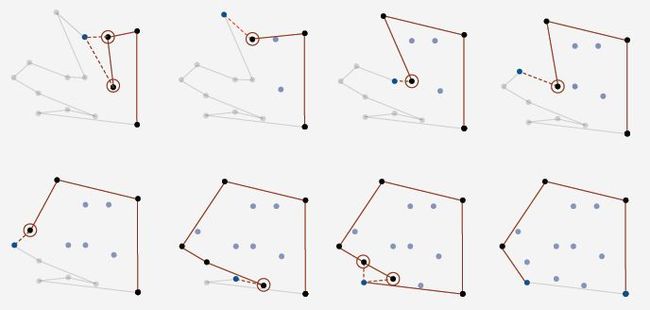
-- Cost of convex hull. N log N + N.
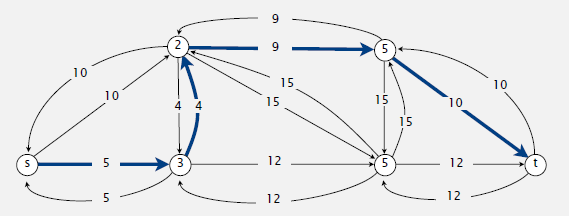
5. Undirected shortest paths (with nonnegative weights) reduces to directed shortest path:
-- Replace each undirected edge by two directed edges.
-- Cost of undirected shortest paths. E log V + E.
-- Can still solve shortest-paths problem in undirected graphs with negative weights (if no negative cycles), but need more sophisticated techniques.(reduces to weighted non-bipartite matching)
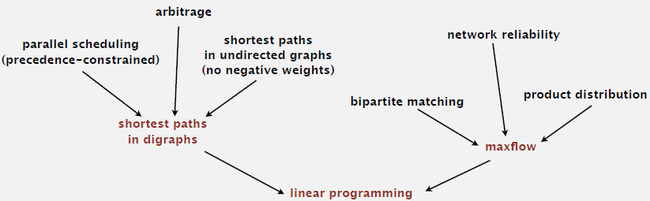
6. Linear-time reductions involving familiar problems:
7. Reduction usage: establishing lower bounds. If I could easily solve Y, then I could easily solve X. If I can’t easily solve X. Therefore, I can’t easily solve Y.
8. Linear-time reductions: Problem X linear-time reduces to problem Y if X can be solved with:
-- Linear number of standard computational steps.
-- Constant number of calls to Y.
9. Sorting linear-time reduces to convex hull.
-- Sorting instance: x1, x2, ... , xN.
-- Convex hull instance: (x1 , x1^2 ), (x2, x2^2 ), ... , (xN , xN^2 ).
-- Region { x : x^2 ≥ x } is convex ⇒ all points are on hull.
-- Starting at point with most negative x, counterclockwise order of hull points yields integers in ascending order.
10. Establishing lower bounds through reduction is an important tool in guiding algorithm design efforts.
11. Reduction usage: Classifying problems. Prove that two problems X and Y have the same complexity
-- show that problem X linear-time reduces to Y.
-- show that Y linear-time reduces to X.
-- Conclude that X and Y have the same complexity. ( even if we don't know what the complexity is!)
12. A possible real-world scenario.
-- System designer specs the APIs for project.
-- Alice implements sort() using convexHull().
-- Bob implements convexHull() using sort().
-- Infinite reduction loop!
13. Integer arithmetic problems with the same complexity as integer multiplication
14. Numerical linear algebra problems with the same complexity as matrix multiplication
15. Summary:
-- Reductions are important in theory to:
- Design algorithms.
- Establish lower bounds.
- Classify problems according to their computational requirements.
-- Reductions are important in practice to:
- Design algorithms.
- Design reusable software modules.
- Determine difficulty of your problem and choose the right tool.