leetcode: Wildcard Matching

问题描述

Implement wildcard pattern matching with support for '?' and '*'.

'?' Matches any single character.
'*' Matches any sequence of characters (including the empty sequence).

The matching should cover the entire input string (not partial).

The function prototype should be:
bool isMatch(const char *s, const char *p)

Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "*") → true
isMatch("aa", "a*") → true
isMatch("ab", "?*") → true
isMatch("aab", "c*a*b") → false

 

原问题链接：https://oj.leetcode.com/problems/wildcard-matching/

 

问题分析

 　　这是一个字符串匹配的问题。看起来和普通的字符串匹配稍微有点不一样的地方就是有两个特殊的字符"?"和"*"。其中"?"表示匹配一个当前的任意字符。而"*"表示匹配当前的若干个字符。如果撇开*号的话，这个问题就挺简单的。因为基本上对于两个串来说，每个字符都是一一对应的，唯一要区分一下的就是"?"这个。当碰到这个字符的时候，让对应位置的字符不管是什么都算匹配就完了。

　　所以，在不考虑"*"的情况下，我们的方法大致结构如下：

boolean isMatch(String s, String p) {
    int l = 0, r = 0;
    while(l < s.length() && r < p.length()) {
        if(s.charAt(l) == p.charAt(r) || p.charAt(r) == '?') {
            l++;
            r++
        } else return false;
    }
    if(l < s.length() || r < p.length()) return false;
    return true;
}

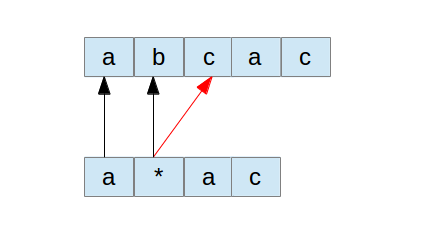
    在前面这部分基础代码思路之上，我们再来考虑一下符号"*"的情况。它的情况之所以比较特殊就是因为当我们的源串s中间某个位置是对应的*号时，这个*号是对应０个或者多个字符的。比如说s = "abaaaac" p = "a*"，这个时候p里的*号对应第一个字符a后面的所有部分。如果s="abc", p = "a*bc"，这个时候可以说*号对应０个字符。所以，这个时候问题的核心就在于，当s和p在某个位置的时候遇到*号，我们不知道s这边的符号要往前多少个才算是一个合理的匹配。在进一步分析前，我们先看看*号匹配的几种情况：

 

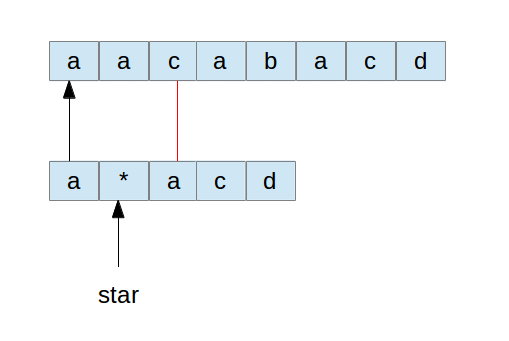
　　上图是*号匹配了前面串中间指定点后面所有的字符。下图是匹配了部分串的情况：

   对于后面这个匹配了部分串的情况，我们会发现一个有意思的地方。就是从模式串p中*号后面的字符起，如果*后面确实有字符，那么要和前面的串匹配，则前面必然有一部分是和它对应上的。否则这个匹配就失败了。那么我们可以这样来看，碰到*号的时候，取*号后面的那个字符，再去和源字符串比较，如果相等，则尝试往后面继续比较。这种情况可以用下图来描述：

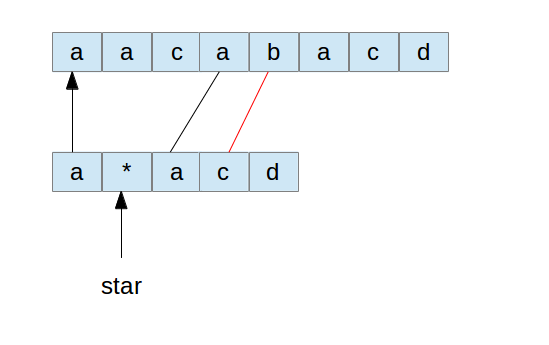
　　在这种情况下，假定star后面的元素和前面的对应元素匹配上了，我们可以认为这是尝试*号匹配０个元素。可是当我们匹配了若干个之后，却发现如下的情景：

    这个时候说明我们*号匹配０个元素并不成立。因为后面的部分没有匹配上。这个时候该怎么办呢？因为我们后面这部分是和前面s串中间刚对应到*号的元素开始的。既然以这个元素为起点和后面的比较不匹配了。我们就尝试它后面的那个元素。所以，后续的比较可以如下：

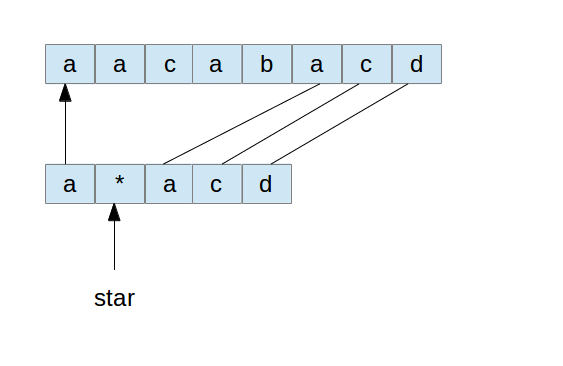
　　这一步也是匹配失败，然后按照前面的方式，假定前面的*号匹配了更多的一个，再从后面一个开始尝试：

 　　按照前面的过程，我们一直到最后得到匹配的结果如下：

 

 　　经过刚才的手工比较过程。我们可以将针对*号的匹配过程总结如下：

１．假设碰到*号时s串的位置是l, p串的位置是r，则将r+1作为*号后续进行比较的起点。

２．从l开始与r+1位置的元素进行比较，如果相同，再按照常规匹配的方式往后面继续比。否则l跳到前面和r+1开始比较那个位置的后面一个。同时p这边的元素也要归位到r+1

　　所以，到了这一步，我们就知道。当遇到*号的时候，先记录一下l所在的位置和r+1所在的位置。每次匹配比较不对了就回退。假设记录l开始比较位置的元素为match。在每次匹配失败后match就要加１，表示下一个开始比较的起点。

３．既然前面匹配的情况讨论了。对于不匹配的情况呢？假设我们碰到一些不匹配的了。如果前面根本就没有*号，这就是正常的字符串比较不匹配的情况，我们直接就返回匹配不成功了。

４．还有一个问题，这算是比较隐蔽一点的情况。因为我们这边是一碰到*号就一直不停的去比较，如果p串中间有多个*号呢？我们可能已经比较到前面s串的结尾了，但是p串后面可能还有一部分字符。这个时候我们也需要进行判断。如果剩下的是*号，则相当于*号匹配了０个元素，否则表示匹配错误。

　　基于上述的讨论，一个典型的实现如下：

public class Solution {
    public boolean isMatch(String str, String pattern) {
        int s = 0, p = 0, match = 0, starIdx = -1;            
        while (s < str.length()){
            // advancing both pointers
            if (p < pattern.length()  && (pattern.charAt(p) == '?' || str.charAt(s) == pattern.charAt(p))){
                s++;
                p++;
            }
            // * found, only advancing pattern pointer
            else if (p < pattern.length() && pattern.charAt(p) == '*'){
                starIdx = p;
                match = s;
                p++;
            }
           // last pattern pointer was *, advancing string pointer
            else if (starIdx != -1){
                p = starIdx + 1;
                match++;
                s = match;
            }
           //current pattern pointer is not star, last patter pointer was not *
          //characters do not match
            else return false;
        }

        //check for remaining characters in pattern
        while (p < pattern.length() && pattern.charAt(p) == '*')
            p++;

        return p == pattern.length();
    }
}

     总的来说，基于上述方法来解决这个问题是一种贪婪算法的思路。因为每次碰到一个*号我们会将它记录下来，然后就去和源串进行比较。这种办法效率比较高，当然，只是很难想到。那么除了这个办法，我们还有没有其他方法呢？

 

其他思路

 　　在我们前面描述解决这个问题的经过时，我们已经发现了一点和递归相关的意思。假设我们两个串，它们在模式串为普通字符或者"?"号的时候，它们两边只要是对应符号相同就表示是匹配的。假设当前两个元素所在的位置分别为l, r。则正好有如下的关系：

if(s[l] == p[r] || p[r] == '?') match(l, r) = match(l-1, r-1) 。

　这是上面递归关系的一部分。然后对于p[r] == '*'的情况呢？我们知道，需要从s串中间l所在位置往后面每个都去尝试。相当于这样的一个关系：

if(p[r] == '*') {

     while(l < s.length()) {

        if(match(l, r)) return true;

        l++;

     }

}

　　　这样我们保证从l位置一直到最后结束部分一直进行比较，直到有一个匹配的。因为这是一个递归的函数定义，它的返回条件则是r == p.length()，表示我们已经遍历到了模式串的结尾了。按照这个思路，得到的代码如下：

boolean isMatch(String s, String p, int l, int r) {
    if(r == p.length()) return l == s.length();
    if(p.charAt(r) == '*') {
        while(p.charAt(r) == '*') r++;   // Move the index at p to a non-start char.
        while(l < s.length()) {
            if(isMatch(s, p, l, r)) return true; // Find one match, return true.
            l++; // Try the next one.
        }
        return isMatch(s, p, l, r);
    } else if(l < s.length() && (p.charAt(j) == '?' || s.charAt(l) == p.charAt(r)))
        return isMatch(s, p, l + 1, r + 1);
    return false;
}

    通过这种递归的关系我们得到的这个算法虽然定义清楚了其中的关系，但是如果去分析它的时间复杂度的话会发现这是一个指数级别的，在实际中执行起来并不理想。那么，有没有办法可以改进一下呢？

 

改进

     我们知道前面的问题在于我们虽然得出了递归的关系，但是执行的效率偏低。这个时候我们可能会想到一个点，就是通常递归的方法执行比较慢的时候，我们去看看它们的递归的关系。是否存在递归过程中对一些结果的重复计算。如果有的话，这就是一个利用动态规划方法的地方。

　　假设我们用F(i, j)表示串s[0...i], p[0...j]这两个串分别到i和j位置它们是否匹配的函数。那么，我们可以得到这样的一个递推关系：

F[i, j] = F[i-1, j-1] &&(s[i] == p[j] || p[j] == '?')  (假设此时p[j] != '*')

F[i, j] = or F[i-1, j-1] for i = 0, ... i-1, 如果p[j] = '*'。这里表示我们从前面开始找到一个对应j-1时为true的情况，表示对应i-1的时候s串匹配的位置，则从这个位置后面所有的位置都是true。

 　所以按照前面的思路，我们可以定义一个二维数组boolean[][] dp = new boolean[s.length()][p.length()]; 参考的实现如下：

 

boolean isMatch(String s, String p) {
    if(p.length() == 0) return s.length() == 0;
    int m = s.length();
    int n = p.length();
    boolean[][] dp = new boolean[m + 1][n + 1];
    dp[0][0] = true;
    for(int j = 0; j < n; j++) {
        if(p.charAt(j) != '*') {
            for(int i = 0; i < m; i++) {
                dp[i + 1][j + 1] = dp[i][j] && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '?');
            }
        } else{
            int i = 0;
            while(i < s.length() && !dp[i][j]) i++;
            for(; i < m; i++) dp[i][j] = true;
        }
    }
    return dp[m][n];
}

 　这种实现方式相对来说性能有了很大的提升，它的时间复杂度为o(m * n)。空间的复杂度也是O(m * n)。实际上，我们还可以对代码做进一步的改进。因为空间计算每次只是用到前一次计算的结果，我们可以将空间的复杂度降低到O(m)。具体的实现这里就不再赘述了。

 

总结

　　对于字符串的模糊匹配问题看起来很简单，实际上牵涉到非常复杂的判断条件。结合不同的场景，最关键的就是要找到它们的递归关系，然后进行动态规划方法的优化。 

 

参考材料

http://yucoding.blogspot.com/2013/02/leetcode-question-123-wildcard-matching.html

http://www.cnblogs.com/codingmylife/archive/2012/10/05/2712585.html

http://tech-wonderland.net/blog/leetcode-wildcard-matching.html

http://blog.csdn.net/linhuanmars/article/details/21198049