转自
http://qing.weibo.com/1765738567/693f0847330008ii.html
http://qing.weibo.com/1765738567/693f0847330008x6.html
讲到了LSM 树和COLA树,LSM已经被许多主流NoSQL系统采用,如BigTable,Cassandra,而COLA则知道的人不多。文章分析比较的很清晰。
以下原文
-----------------------------------------------------------------------------------------------------------------------------------
首先来回答一个问题:为什么在磁盘中要使用b+树来进行文件存储呢?
原因还是因为树的高度低得缘故,磁盘本身是一个顺序读写快,随机读写慢的系统,那么如果想高效的从磁盘中找到数据,势必需要满足一个最重要的条件:减少寻道次数。
我们以平衡树为例进行对比,就会发现问题所在了:
先上个图
这是个平衡树,可以看到基本上一个元素下只有两个子叶节点
抽象的来看,树想要达成有效查找,势必需要维持如下一种结构:
树的子叶节点中,左子树一定小于等于当前节点,而当前节点的右子树则一定大于当前节点。只有这样,才能够维持全局有序,才能够进行查询。
这也就决定了只有取得某一个子叶节点后,才能够根据这个节点知道他的子树的具体的值情况。这点非常之重要,因为二叉平衡树,只有两个子叶节点,所以如果想找到某个数据,他必须重复更多次“拿到一个节点的两个子节点,判断大小,再从其中一个子节点取出他的两个子节点,判断大小。”这一过程。
这个过程重复的次数,就是树的高度。那么既然每个子树只有两个节点,那么N个数据的树的高度也就很容易可以算出了。
平衡二叉树这种结构的好处是,没有空间浪费,不会存在空余的空间,但坏处是需要取出多个节点,且无法预测下一个节点的位置。这种取出的操作,在内存内进行的时候,速度很快,但如果到磁盘,那么就意味着大量随机寻道。基本磁盘就被查死了。
而b树,因为其构建过程中引入了有序数组,从而有效的降低了树的高度,一次取出一个连续的数组,这个操作在磁盘上比取出与数组相同数量的离散数据,要便宜的多。因此磁盘上基本都是b树结构。
不过,b树结构也不是完美的,与二叉树相比,他会耗费更多的空间。在最恶劣的情况下,要有几乎是元数据两倍的格子才能装得下整个数据集(当树的所有节点都进行了分裂后)。
以上,我们就对二叉树和b树进行了简要的分析,当然里面还有非常多的知识我这里没有提到,我希望我的这个系列能够成为让大家入门的材料,如果感兴趣可以知道从哪里着手即可。如果您通过我的文章发现对这些原来枯燥的数据结构有了兴趣,那么我的目标就达到了: )
在这章中,我们还将对b数的问题进行一下剖析,然后给出几个解决的方向
其实toku DB的网站上有个非常不错的对b树问题的说明,我在这里就再次侵权一下,将他们的图作为说明b树问题的图谱吧,因为真的非常清晰。
http://tokutek.com/downloads/mysqluc-2010-fractal-trees.pdf
B树在插入的时候,如果是最后一个node,那么速度非常快,因为是顺序写。
但如果有更新插入删除等综合写入,最后因为需要循环利用磁盘块,所以会出现较多的随机io.大量时间消耗在磁盘寻道时间上。
-----------------------------------------------------------------------------------------------------------------------------------
PS:B+树就是在B树基础上加两个规定 1.非叶子结点只存指针,叶子结点存数据 2.所有叶子结点从左到右用双链表串起来
-----------------------------------------------------------------------------------------------------------------------------------
如果是一个运行时间很长的b树,那么几乎所有的请求,都是随机io。因为磁盘块本身已经不再连续,很难保证可以顺序读取。
以上就是b树在磁盘结构中最大的问题了。
那么如何能够解决这个问题呢?
目前主流的思路有以下几种
1. 放弃部分读性能,使用更加面向顺序写的树的结构来提升写性能。
这个类别里面,从数据结构来说,就我所知并比较流行的是两类,
一类是COLA(Cache-Oblivious Look ahead Array)(代表应用自然是tokuDB)。
一类是LSM tree(Log-structured merge Tree)或SSTABLE
(代表的数据集是cassandra,hbase,bdb java editon,levelDB etc.).
2. 使用ssd,让寻道成为往事。
我们在这个系列里,主要还是讲LSM tree吧,因为这个东西几乎要一桶浆糊了。几乎所有的nosql都在使用,然后利用这个宣称自己比mysql的innodb快多少多少倍。。我对此表示比较无语。因为nosql本身似乎应该是以省去解析和事务锁的方式来提升效能。怎么最后却改了底层数据结构,然后宣称这是nosql比mysql快的原因呢?
毕竟Mysql又不是不能挂接LSM tree的引擎。。。
好吧,牢骚我不多说,毕竟还是要感谢nosql运动,让数据库团队都重新审视了一下数据库这个产品的本身。
那么下面,我们就来介绍一下LSM Tree的核心思想吧。
首先来分析一下为什么b+树会慢。
从原理来说,b+树在查询过程中应该是不会慢的,但如果数据插入比较无序的时候,比如先插入5 然后10000然后3然后800 这样跨度很大的数据的时候,就需要先“找到这个数据应该被插入的位置”,然后插入数据。这个查找到位置的过程,如果非常离散,那么就意味着每次查找的时候,他的子叶节点都不在内存中,这时候就必须使用磁盘寻道时间来进行查找了。更新基本与插入是相同的
那么,LSM Tree采取了什么样的方式来优化这个问题呢?
简单来说,就是放弃磁盘读性能来换取写的顺序性。
乍一看,似乎会认为读应该是大部分系统最应该保证的特性,所以用读换写似乎不是个好买卖。但别急,听我分析之。
1. 内存的速度远超磁盘,1000倍以上。而读取的性能提升,主要还是依靠内存命中率而非磁盘读的次数
2. 写入不占用磁盘的io,读取就能获取更长时间的磁盘io使用权,从而也可以提升读取效率。
因此,虽然SSTable降低了了读的性能,但如果数据的读取命中率有保障的前提下,因为读取能够获得更多的磁盘io机会,因此读取性能基本没有降低,甚至还会有提升。
而写入的性能则会获得较大幅度的提升,基本上是5~10倍左右。
下面来看一下细节
其实从本质来说,k-v存储要解决的问题就是这么一个:尽可能快得写入,以及尽可能快的读取。
让我从写入最快的极端开始说起,阐述一下k-v存储的核心之一—树这个组件吧。
我们假设要写入一个1000个节点的key是随机数的数据。
对磁盘来说,最快的写入方式一定是顺序的将每一次写入都直接写入到磁盘中即可。
但这样带来的问题是,我没办法查询,因为每次查询一个值都需要遍历整个数据才能找到,这个读性能就太悲剧了。。
那么如果我想获取磁盘读性能最高,应该怎么做呢?把数据全部排序就行了,b树就是这样的结构。
那么,b树的写太烂了,我需要提升写,可以放弃部分磁盘读性能,怎么办呢?
简单,那就弄很多个小的有序结构,比如每m个数据,在内存里排序一次,下面100个数据,再排序一次……这样依次做下去,我就可以获得N/m个有序的小的有序结构。
在查询的时候,因为不知道这个数据到底是在哪里,所以就从最新的一个小的有序结构里做二分查找,找得到就返回,找不到就继续找下一个小有序结构,一直到找到为止。
很容易可以看出,这样的模式,读取的时间复杂度是(N/m)*log2N 。读取效率是会下降的。
这就是最本来意义上的LSM tree的思路。
那么这样做,性能还是比较慢的,于是需要再做些事情来提升,怎么做才好呢?
于是引入了以下的几个东西来改进它
1. Bloom filter : 就是个带随即概率的bitmap,可以快速的告诉你,某一个小的有序结构里有没有指定的那个数据的。于是我就可以不用二分查找,而只需简单的计算几次就能知道数据是否在某个小集合里啦。效率得到了提升,但付出的是空间代价。
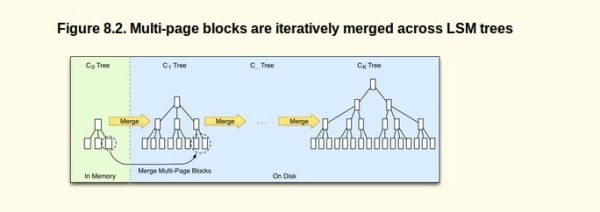
2. 小树合并为大树: 也就是大家经常看到的compact的过程,因为小树他性能有问题,所以要有个进程不断地将小树合并到大树上,这样大部分的老数据查询也可以直接使用log2N的方式找到,不需要再进行(N/m)*log2n的查询了。
这就是LSMTree的核心思路和优化方式。
不过,LSMTree也有个隐含的条件,就是他实现数据库的insert语义时性能不会很高,原因是,insert的含义是: 事务中,先查找该插入的数据,如果存在,则抛出异常,如果不存在则写入。这个“查找”的过程,会拖慢整个写入。
这样,我们就又介绍了一种k-v写入的模型啦。在下一次,我们将再去看看另外一种使用了类似思路,但方法完全不同的b树优化方式 COLA树系。敬请期待 ~
-------------------------------
COLA树
-------------------------------
终于来到了COLA树系,这套东西目前来看呢,确实不如LSM火,不过作为可选方案,也是个值得了解的尝试,不过这块因为只有一组MIT的人搞了个东西出来,所以其实真正的方案也语焉不详的。
从性能来说,tokuDB的写入性能很高,但更新似乎不是很给力,查询较好,占用较少的内存。
http://www.mysqlperformanceblog.com/2009/04/28/detailed-review-of-tokutek-storage-engine/
这里有一些性能上的指标和分析性文字。确实看起来很心动,不过这东西只适合磁盘结构,到了SSD似乎就挂了。原因不详,因为没有实际的看过他们的代码,所以一切都是推测,如果有问题,请告知我。
先说原理,上ppt http://tokutek.com/presentations/bender-Scalperf-9-09.pdf,简单来说,就是一帮MIT的小子们,分析了一下为什么磁盘写性能这么慢,读的性能也这么慢,然后一拍脑袋,说:“哎呀,我知道了,对于两级的存储(比如磁盘对应内存,或内存对于缓存,有两个属性是会对整个查询和写入造成影响的,一个是容量空间小但速度更快的存储的size,另外一个则是一次传输的block的size.而我们要做的事情,就是尽可能让每次的操作传输尽可能少的数据块。
传输的越少,那么查询的性能就越好。
进而,有人提出了更多种的解决方案。
•B-tree [Bayer, McCreight 72]
• cache-oblivious B-tree [Bender, Demaine, Farach-Colton 00]
• buffer tree [Arge 95]
• buffered-repositorytree[Buchsbaum,Goldwasser,Venkatasubramanian,Westbrook 00]
• Bε
tree[Brodal, Fagerberg 03]
• log-structured merge tree [O'Neil, Cheng, Gawlick, O'Neil 96]
• string B-tree [Ferragina, Grossi 99]
这些结构都是用于解决这样一个问题,在磁盘上能够创建动态的有序查询结构。
在今天,主要想介绍的就是COLA,所谓cache-oblivious 就是说,他不需要知道具体的内存大小和一个块的大小,或者说,无论内存多大,块有多大,都可以使用同一套逻辑进行处理,这无疑是具有优势的,因为内存大小虽然可以知道,但内存是随时可能被临时的占用去做其他事情的,这时候,CO就非常有用了。
其他我就不多说了,看一下细节吧~再说这个我自己都快绕进去了。
众所周知的,磁盘需要的是顺序写入,下一个问题就是,怎么能够保证数据的顺序写。
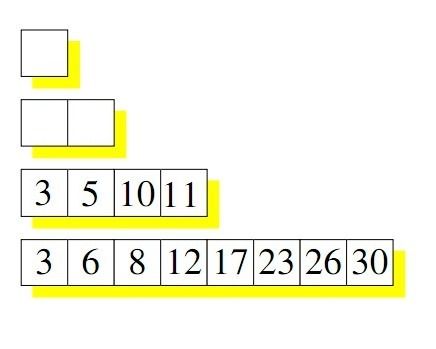
我们假定有这样一个空的数据集合
可以认为树的高度是log2N。
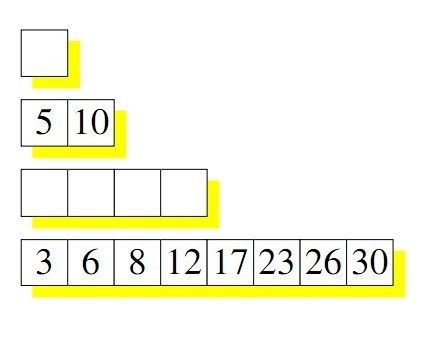
每行要么就是空的,要么就是满的,每行数据都是排序后的数据。
如果再写一个值的时候,会写在第一行,比如写了3。
再写一个值11的时候,因为第一行已经写满了,所以将3取出来,和11做排序,尝试写第二行。又因为第二行也满了,所以将第二行的5和10也取出,对3,11,5,10 进行排序。写入第四行
这就是COLA的写入过程。
可以很清楚的看出,COLA的核心其实和LSM类似,每次“将数据从上一层取出,与外部数据进行归并排序后写入新的array”的这个操作,对sas磁盘非常友好。因此,写入性能就会有非常大的提升。
并且因为数据结构简单,没有维持太多额外的指针,所以相对的比较节省空间。
但这样查询会需要针对每个array都进行一次二分查找。
性能似乎还不是很高,所以,他们想到了下面这种方式,把它的命名为fractal tree,分形树。
用更简单的方法来说的话呢,就是在merge的时候,上层持有下层数据的一个额外的指针。
来协助进行二分查找。
这样,利用空间换时间,他的查询速度就又回到了log2N这个级别了。
到此,又一个有序结构被我囫囵吞枣了。
嘿嘿