【计算机系统学习-信息表示和处理】【一、信息的存储】

最近在深入学习计算机系统。很多的基础都忘记了。所以现在复习了一遍。

教材是《深入理解计算机系统》英文简写《CSAPP》

1、首先，无论是什么信息，在计算机中的表示都是0，和1组成的。那么这些0和1是怎么存储的呢?

当然，0和1只是一个表示符号，我们在实际中，可能用电位高低表示0和1，或者用时光盘的凸凹等等。

我们现在要说的，是抽象了一个层次的，就是这些无论如何表示0和1的信息，如何在计算机中存储的？

内存，你也许第一反应。对，信息是存储在内存中的，对于机器及程序来说，他把一个巨大的数组看做是一个虚拟存储器，而且，大多数的计算机都把这个虚拟存储器以8位来分一个块。每个块标识一个地址，这些地址组合起来形成虚拟地址空间。然后呢，我们的内存条，通过操作系统和她自身硬件的结合，来实现了我们对虚拟存储器的构想，使她看上去就是一个字节数组。

2、进制转换。由于我们熟悉的十进制在只有0和1的计算机世界里不能表示了，于是我们就用二进制吧。

例如： 十进制数 8 的二进制表示为 1000，十进制数 98的二进制表示为 1100010

这样的表示可能在我们看来很费解，但是计算机只能这么表示。而我们呢，需要定义一些法则来使得计算机能理解这些数字。

下面我们看一下二进制和十进制是如何转换的：

二进制到十进制

例如二进制 1100010

十进制到二进制转换

98 = 49* 2 + 0

49 = 24* 2 + 1

24 = 12* 2 + 0

12 = 6* 2 +0

6 =3 * 2 + 0

3 = 1* 2 + 1

1 = 0 *1 +1

所以，

是不是感觉比较复杂，其实也不是，当时，为了这种转换更简单，我们用16进制代替10进制，因为从2进制到16进制的转换更容易。

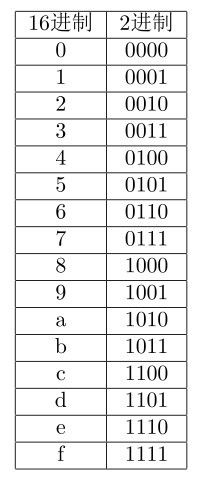
首先16进制是使用0,1,2,3，……，9，a,b,c,d,e,f十六个符号表示的。一般在c语言中，使用0x开头表示十六进制，例如0x57E8b

这里对于A-F，大小写都可以。那么二进制如何与16进制转换呢？

看下表：

我们只要对照上表，把每个字符用二进制位表示就行了。

例如 0x5a = 01011010(2)

虚拟存储和进制的问题都完了，现在我们需要考虑，如何表示一个整数呢？

3，字长。(word size)一个机器的字长，指明了整数和指针的标准大小。所以字长决定了虚拟空间地址的大小。

一个字长为n的机器，可以编码的虚拟地址空间就是2ⁿ - 1 (从0开始）。我们目前大多数的32位机器（如果是64位的，装了32位的操作系统的话，字长也只能看做是32位）的虚拟地址空间最大就是4GB。

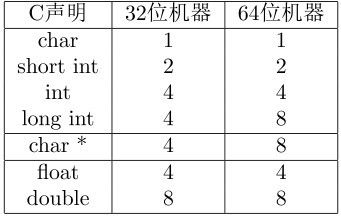
知道了字长，下面我们要看数据了。一般而言，不同的语言有不同的数据类型。c语言的整数类型，就是用一个字长来表示。在32位机器上，就是32位，4字节。事实上，不同的数据类型可能使用不同的位长度来表示。下面是c语言在不同字长机器上的数据类型长度。

以字节为单位。

使用c函数

sizeof(int) sizeof(char) sizeof(float) sizeof(double) sizeof(void*)

sizeof(int)可以查看int在相应的机器上需要的字节数。当然也可以用sizeof(void *), sizeof(float),sizeof(double)

由上表可知，int和char *在32位机器上有相同的字节长度。很多时候，我们使用一个int来存放一个指针，而这样的程序如果移植到64位机器上，就会出问题了。

现在我们了解数据类型的大小了，但是我们的虚拟存储单位是byte的，如果要存一个int型数据，那么需要4个byte，这就产生一个问题，这4个byte中存放数据的顺序问题。

设 int d = 0x01234567,我们存放的地址是 0x100,0x101,0x102,0x103 这4个byte单元中。则有以下两种方法。

大端法(big endian)

小端法(little endian)

IBM ,Motorola 使用的大端法，Intel的多数使用小端。关于我们的机器大端还是小端，我们可以写个小程序测试。

//待插入程序

#include<stdio.h> int main(void) { int i = 0x1234567; char *p = (char*)&i; if(*p == 0x1) printf("Your machine is big endian!/n"); else printf("Your machine is little endian!/n"); return 0; }

在网络数据传输时，如果大端小端各自为政，就会出大问题了。所以我们有网络字节码。

为了方便学习，我们可以用下面的代码来查看各种数据是如何存储的。

#include<stdio.h> /*the beginning of the bytes which we will show them*/ typedef unsigned char *byte_pointer; void show_bytes(byte_pointer start, int len) { int i; for ( i = 0; i < len; i++) { printf(" %.2x", start[i]); printf("/n"); } } void show_int(int x) { show_bytes((byte_pointer)&x, sizeof(int)); } void show_float(float x) { show_bytes((byte_pointer)&x, sizeof(float)); } void show_pointer(void *x) { show_bytes((byte_pointer)&x, sizeof(void *)); }

//待插入程序

太晚了，先睡觉。

只能这样编辑了。

有了上面的程序，我们就可以以字节为单位来看数据了。下面马上来一个测试程序

void show_bytes_test(int val) { int ival = val; float fval = (float)fval; int *pval = &ival; show_int(ival); show_float(fval); show_pointer(pval); }

随便输入一个数字测试吧。记住，我们打印出来的是以16进制表示的。%.2x就是用两个16进制字符表示。

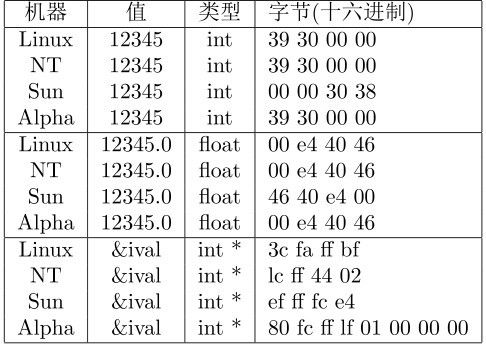
程序就不多说。看效果吧。例如我们输入12345，十六进制表示为 0x00003039

我们的测试使用Linux系统，WindowsNT,Sun主机，Alpha主机

这下明白了。注意int和float的表示看起来很不同，如果你把他们的二进制形式写出来，你会有发现的。这是后话。

留在IEEE浮点表示时再说。

位操作

由于计算机使用的是二进制表示，我们的编程语言也提供了相应的位操作。这就是位运算。

四种运算

1、~运算，求反。 ~0 = 1 ； ~1=0

2、&与运算。 1&1 = 1；1&0 = 0 ； 0&1 = 0； 0&0 = 0

3、|或运算。 1|1 = 1； 1|0 = 1； 0|1 = 1； 0|0 = 0

4、^异或运算。 0^0 =0； 1^1 = 0; 0^1 = 1 ; 1^0 =1

这些运算和布尔代数类似，但是我们要分清位运算和逻辑运算。下面是逻辑运算

1、！运算Not 。 ！0 = 1， ！5 =0

2、&& 运算And

3、| 运算OR

4、⊕ 运算 EXCLUSIVE-OR

逻辑运算不用转换为二进制，而是对表达式判断真假。

使用位运算和逻辑运算，我们可以表达一个 x==y这样的判断。大家可以先考虑下如何用位和逻辑运算表达。

我们常用位运算来实现掩码运算。例如在网络中通过子网掩码来确定网络地址。

这就是如果我们想要得到一个字节中的某几位（高位或者低位）的有效字节。例如0xFF，这个掩码表示一个低位有效字节。

使用 x & 0xFF就可以把x的高位字节置零，只留下低位字节。

注意，如果我们需要高位的有效位，那么我们的掩码可能写成 0xFFFF0000，但是这样的掩码只对32位的机器起作用。

我们可以这样写，~0xFFFF，这样生成的掩码将可被移植到不同位的机器上。

位运算还有位移运

左移 右边补零。每移动k位，可以看成 乘以 2^k

算术右移 左边补符号位（这将要在下面讲到）

逻辑右移 左边补零。

移位运算可以大大提高性能。例如 x*7 这样的乘法运算，我们可以 用 x <<3- x来代替。这样性能将会大大改善。

上面我们展示了int，float等在内存中的表示，现在我们来看看这些整数是如何被编码的，比如，如何表示一个负数，还有两个

int数相加是否和我们在纸上运算的一样？

请看下一篇：整数的表示